4.3. Методы представления графов в аналитической форме

Рассмотрим пример построения графа. Пусть множество вершин определено, как V = {a, b, c, d}, а множество ребер, как X = {1, 2, 3, …, 7}. Пусть инцидентор графа Р определен девятью значениями: P (a,1,a); P (a,2,b); P (b,3,a); P (a,3,b); P (a,4,c); P (a,5,c); P (c,5,a); P (c,6, b); P (b, 7,c) – которые истинны, остальные ложны. Изображение графа представлено на рис. 4.8. В данном примере вершины а, b, и с – смежные, а вершина d – изолированная, т.е. не инцидентна ни одному ребру.

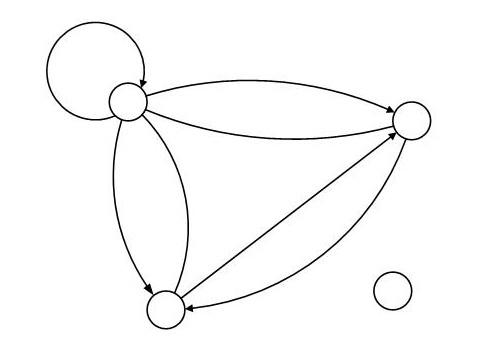1

2

а

3 b

4 5

6

7

d

c

Рис. 4.8

Существуют и другие способы задания графов. Рассмотрим еще один пример: пусть задано изображение неориентированного графа G (рис. 4.9а) и подобного ему орграфа G_О (рис. 4.9б). Пусть v₁, v₂, ... v₅ – вершины, а х₁, х₂, ... х₆ – ребра (дуги). Графы G и G_О можно представить в аналитической форме либо матрицей смежности A, либо матрицей инцидентности B.

v₄ х₂ v₃ v₄ х₂ v₃

х₃ х₅ х₃ х₅

х₁ v₂ х₄ х₁ v₂ х₄

v₅ х₆ v₅ х₆

v₁ v₁

а) б)

Рис. 4.9

Матрицей инцидентности графа G называется матрица B = ||b_ij||, имеющая i=1, .., n столбцов и j = 1, ..., m строк, что соответствует количеству вершин n и количеству ребер m. Элемент матрицы b_ij = 1, если вершина v_i инцидентна ребру х _j, и b_ij = 0, если не инцидентна. Для ориентированного графа элемент матрицы b_ij = 1, если дуга исходит из вершины, и b_ij = –1, если дуга заходит в вершину. Если в орграфе есть петля, то b_ij = 2. Для неориентированного графа и орграфа, представленных на рис. 4.9а и б, матрицы инцидентности выглядят соответственно следующим образом:

v₁, v₂, v₃, v₄, v₅ v₁, v₂, v₃, v₄, v₅

1 1 0 0 0 х₁ 1 -1 0 0 0 х₁

0 1 1 0 0 х₂ 0 1 -1 0 0 х₂

B(G) = 0 1 1 0 0 х₃ B(G_О) = 0 -1 1 0 0 х₃

0 1 0 0 1 х₄ 0 1 0 0 -1 х₄

0 0 1 0 1 х₅ 0 0 -1 0 1 х₅

0 0 0 0 1 х₆ 0 0 0 0 2 х₆

В каждой строке матрицы инцидентности только два элемента (или один) отличны от нуля. По матрице инцидентности можно определить степени всех вершин графа. При этом для петель значение удваивается.

Матрицей смежности графа G называется квадратная матрица A=||a_ij||, столбцам и строкам которой соответствуют вершины графа i=1,...,n; j = 1, ..., n. Для неориентированного графа элемент матрицы a_ij равен числу ребер, инцидентных вершинам v_i и v_j, для орграфа – количеству ребер с началом в вершине v_i и концом в вершине v_j. Для нашего примера матрицы смежности будут

v₁, v₂, v₃, v₄, v₅ v₁, v₂, v₃, v₄, v₅

0 1 0 0 0 v₁ 0 0 0 0 0 v₁

1 0 2 0 1 v₂ 1 0 1 0 0 v₂

A(G) = 0 2 0 0 1 v₃ A(G_О) = 0 1 0 0 1 v₃

0 0 0 0 0 v₄ 0 0 0 0 0 v₄

0 1 1 0 1 v₅ 0 1 0 0 1 v₅

Как видно, матрица смежности для неориентированного графа симметрична, а для орграфа – необязательно. Орграф с симметричной матрицей смежности канонически соответствует неорграфу с такой же матрицей смежности.

Итак, графы могут быть заданы тремя способами:

1. Непосредственным заданием множеств вершин V и ребер X , а также отношением инцидентности.

2. Матрицей смежности или матрицей инцидентности.

3. Графическим изображением (рисунком).

Как определить, что данные два графа одинаковы? Для первых двух способов задания ответ прост: когда совпадают их описания – списки вершин и ребер или матрицы. По рисунку определить, одинаковы ли графы, сложнее. Один и тот же граф можно изобразить разными рисунками (рис. 4.10), по-разному расположив вершины и придав ребрам разную геометрическую форму и длину. С другой стороны, два одинаковых, на первый взгляд, рисунка могут задавать разные графы, если у них различная нумерация вершин, из-за чего матрицы смежности и списки ребер у них будут различны (рис. 4.11).

Рис. 4.10 Рис. 4.11

Графы, которые отличаются только нумерацией вершин (и которые с помощью перенумерации можно сделать одинаковыми), называются изоморфными. Изоморфизм графов с небольшим числом вершин иногда очевиден. Однако в общем случае проблема установления изоморфизма графов оказывается сложной в вычислительном отношении задачей.