Кручение стержней

Пусть стержень нагружен произвольной крутящей нагрузкой. Вырежем на некотором расстоянии zбесконечно малый элементdz(рис.44). На данный элемент действует внешняя нагрузка и внутренние крутящие моменты в сечениях, по которым вырезан элемент.

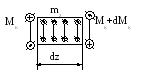
Рис.44

Составим уравнение равновесия вырезанного элемента.

- М_к+m_zdz+ М_к+dМ_к= 0,

,

М_к’ +m_z = 0. (94)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

M_к(z) =C-(95)

Определим физический смысл постоянной интегрирования. При z=0

М_к(0)=C.

Значение интеграла зависит от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенный момент (рис.44):

a

z

Рис.44

при zaФ_м(z)=0

при zaФ_м(z)=-L

б) распределенная нагрузка (рис.45):

m

с

z

Рис.45

при zcФ_м(z)=0

при zcФ_м(z)=-m(z-c)

Пример.

Для приведённой схемы нагружения прямого стержня (рис.46) построить эпюру крутящего момента при следующих исходных данных: m_z= 10 кН/м,L= 10 кНм,

l= 1 м.

Решение.

В соответствии со схемой нагружения запишем уравнение крутящего момента в следующем виде:

M_k (z) =M_k (0) │₁-L│₂-m_z(z-2l) │₃ .

Исходя из условий закрепления стержня, запишем следующее граничное условие:M_k (0) = 0 (реакция незакреплённого конца стержня равна нулю).

Рис.46

Таким образом, записанное уравнение не содержит неизвестных величин и можно приступать к построению графика. Построение графика будем производить аналогично построению графика в примере 1.

1 участок - 0 ≤ z≤l:

M_k (0) = 0 кНм,

M_k (l) = 0 кНм.

2 участок - l≤z≤ 2l:

M_k (l) = 0 – 10 = -10 кНм,

M_k (2l) = 0 – 10 = -10 кНм.

3 участок - 2l≤z≤ 3l:

M_k (2l) = 0 – 10 – 10(2 – 2) = - 10 кНм,

M_k (3l) = 0 – 10 – 10(3 – 2) = -20 кНм.

По рассчитанным значениям строится график крутящего момента (рис. 46).

Изгиб стержней.

Пусть стержень нагружен произвольной поперечной нагрузкой. Вырежем на некотором расстоянии zбесконечно малый элементdz(рис.47). На данный элемент действует внешняя нагрузка и внутренние поперечные силы и изгибающие моменты в сечениях, по которым вырезан элемент.

q_z

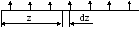
q_у

Q_y

Q_y+dQ_y

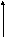
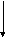
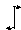
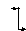
M_x+dM_x

M_x

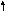
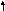
dz

Рис.47

Составим уравнения равновесия вырезанного элемента.

Уравнение равновесия всех сил на вертикальную ось.

- Q_y+q_ydz+Q_y+dQ_y= 0,

,

Q_y’ +q_y = 0. (96)

Уравнение равновесия моментов относительно центра тяжести правого сечения вырезанного элемента.

- М_х+q_ydzdz/2 + М_х+dМ_х-Q_ydz= 0,

слагаемое, выражающее момент от распределенной нагрузки, второго порядка малости, поэтому им можно пренебречь

,

М_х’ =Q_y. (97)

Объединяя дифференциальные уравнения (96) и (97), получим:

М_х'' = -q_y (98)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

М_х(z) =C₁+С₂z– Ф_м,

где Ф_м– частное решение, отражающее внешнюю приложенную нагрузку.

Определим физический смысл постоянных интегрирования. При z=0

М_х(0) =C₁,

М_х’(0) =Q_y(0) = С₂.

Рассмотрим подробнее частное решение. Пусть стержень нагружен произвольной распределенной нагрузкой (рис.48). Определим величину поперечной силы и изгибающего момента для точки с координатой z.

Рис.48

Q_y=,

М_х=. (99)

Значения интегралов зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенная сила (рис.49):

Рис.49

при zaФ_Q(z)=0

Ф_М(z)=0

при zaФ_Q(z)=-P

Ф_М(z)=-P(z-a)

б) распределенная нагрузка (рис.50):

Рис.50

при zcФ_Q(z)=0

Ф_М(z)=0

при zcФ_Q(z)=-q(z-c)

Ф_М(z)=-q(z-c)²/2

в) сосредоточенный момент (рис.51):

Рис.51

при zbФ_Q(z)=0

Ф_М(z)=0

при zbФ_Q(z)=0

Ф_М(z)=-L

Пример.

Для заданной схемы нагружения стержня (рис.52) построить эпюры поперечной силы Q_y(z) и изгибающего моментаM_x(z) при следующих исходных данных:L= 5 кНм,P= 10 кН, q = 20 кН/м,l= 1 м.

Рис.52

Решение.

Запишем уравнения поперечных сил и изгибающего момента:

Q_y(z) =Q_y(0) │₁–P-q(z-l) │₂

M_x(z) =M_x(0) +Q_y(0)z│₁-P(z-l) -q(z-l)²/2│₂

В соответствии с условиями закрепления стержня запишем граничные условия в следующем виде: M_x (0) = -L,

M_x (3l) = 0.

Для нахождения неизвестной реакции Q_y(0) необходимо приравнять уравнение изгибающего момента к нулю при координатеz= 3l:

M_x (3l) = M_x (0) + Q_y (0)3l - P(3l - l) - q(3l - l)²/2 = 0.

Решая это уравнение относительно Q_y(0), получимQ_y(0) = 21.67кН.

Теперь, учитывая найденные константы, уравнения интегральных характеристик можно переписать в следующем виде:

Q_y(z) = 21.67│₁–P–q(z-l) │₂

M_x(z) = -L+ 21.67z│₁–P(z-l) –q(z-l)²/2│₂

Построение графиков будем производить аналогично примеру 1.

1 участок 0 ≤ z≤l:

Q_y(0) = 21.67 кН,

Q_y(l) = 21.67 кН,

M_x (0) = -5 кНм,

M_x (l) = -5 + 21.67*1 = 16.67 кНм.

2 участок l≤z≤ 3l:

Q_y(l) = 21.67 – 10 = 11.67 кН,

Q_y(3l) = 21.67 – 10 – 20*(3 - 1) = -28.33 кН,

M_x (l) = -5 + 21.67*1 – 10(1 – 1) – 20(1 – 1) = 16.67 кНм,

M_x (3l) = -5 + 21.67*3 – 10(3 – 1) – 20(3 – 1) =0 кНм.

Определим координаты экстремума и значения функции изгибающего момента в экстремальной точке:

Q_y(z1) = 21.67 –P–q(z1 -l) = 0 →z1 = 1.58 м.

M_x(1.58) = -L+ 21.67·1.58 –P(1.58 -l) –q(1.58 -l)²/2 = 20.07 кНм.

По рассчитанным значениям строятся графики поперечной силы и изгибающего момента (рис. 52).