
- •В.А. Панов математические основы теории систем. Методы оптимизации
- •Содержание
- •1. Основные понятия и определения 6
- •2. Линейное программирование 13
- •3. Нелинейное программирование 53
- •4. Вариационное исчисление 91
- •5. Оптимальное управление 109
- •Введение
- •1. Основные понятия и определения
- •1.1. Оптимизационная задача
- •1.2. Допустимое решение
- •1.6.1. Частные критерии
- •1.6.2. Обобщенные критерии
- •Обобщенный аддитивный критерий
- •Обобщенный мультипликативный критерий
- •1.6.3. Минимаксные критерии
- •1.7. Общая характеристика методов поиска экстремума
- •Краткая характеристика методов и задач
- •2. Линейное программирование
- •2.1. Стандартный вид задачи линейного программирования (злп)
- •2.2. Способы приведения задачи линейного программирования к стандартному виду
- •2.3. Графический метод решения задач линейного программирования
- •2.4. Симплекс-метод решения задач линейного программирования
- •2.4.1. Канонический вид злп
- •2.4.2. Симплекс-таблица, соответствующая каноническому виду
- •2.4.3. Нахождение координат вершины допустимого многогранника по каноническому виду (симплекс-таблице)
- •2.4.4. Алгоритм решения злп с помощью симплекс-метода
- •Задание для самостоятельной работы
- •2.5. Приведение злп к каноническому виду
- •2.5.1. Метод искусственного базиса
- •2.6. Алгоритм двойственного симплекс-метода
- •Задания для самостоятельной работы
- •2.7. Целочисленное линейное программирование
- •2.7.1. Метод сечения Гомори
- •2.8. Транспортная задача
- •2.8.1. Постановка задачи
- •2.8.2. Математическое описание задачи
- •2.8.3. Транспортная таблица
- •2.8.4. Таблица издержек
- •2.8.5. Метод «северо-западного» угла
- •2.8.6. Алгоритм решения транспортной задачи
- •Задания для самостоятельной работы
- •3. Нелинейное программирование
- •3.1.2.2 Метод ненаправленного поиска
- •3.1.2.3. Метод дихотомии (деление отрезка пополам)
- •3.1.2.4. Метод «золотого сечения»
- •3.1.2.5. Метод Фибоначчи
- •Задание для самостоятельного решения
- •3.2. Графический метод решения задач нелинейного программирования
- •Целевая функция линейная, ограничения нелинейны
- •Ограничения линейные, целевая функция нелинейна
- •3.3. Задачи дробно-линейного программирования
- •Задания для самостоятельного решения
- •3.4. Методы поиска безусловного экстремума функции многих переменных
- •3.4.1. Аналитический метод
- •3.4.2. Итерационные методы
- •3.4.2.1. Метод покоординатного спуска
- •3.4.2.2. Метод наискорейшего спуска
- •Задания для самостоятельной работы
- •3.5. Решение задач нелинейного программирования с ограничениями-равенствами
- •Метод неопределенных множителей Лагранжа
- •Задание для самостоятельной работы
- •3.6. Задачи квадратичного программирования
- •Задания для самостоятельной работы
- •3.7. Метод условного градиента
- •5. X1, x2,xn 0. (3.25)
- •X1, x2,xn 0.
- •Задания для самостоятельной работы
- •3.8. Метод штрафных функций
- •4. Вариационное исчисление
- •4.1. Формула Эйлера-Лагранжа
- •4.2. Частные случаи формулы Эйлера
- •4.3. Обобщенная задача вариационного исчисления
- •4.4. Решение задач вариационного исчисления с ограничениями
- •4.5. Изопериметрическая задача
- •4.6. Функционалы, зависящие от производных высших порядков
- •Задание для самостоятельного решения
- •5. Оптимальное управление
- •5.1. Постановка задачи
- •5.2. Классификация задач оптимального управления
- •5.3. Принцип максимума Понтрягина
- •5.4. Задача о максимальном быстродействии
- •Задания для самостоятельного решения
- •Список литературы
- •Основы теории оптимизации в.А. Панов
Задание для самостоятельной работы
Найти условный экстремум методом неопределенного линейного программирования.
1. z = x1∙x22 x33 2. z = x1 – 2x2 +2x3
при x1+x2+ x3 = 12 при x12+ x22+x3 2 = 9
3. z = x12+ x22 4. z = x12+ x22 + x32 →min
при x1 + x2 = 5 при x1+x2+ x3 ≤ 12
x1, x2 , x3 ≥ 0
5. z = x1∙x2∙x3 6. z = 2x1 + 3x22 +x32
при x1+x2+ x3 = 5 при x1+ x2+x3 = 8
x1∙x2 + x2∙x3 + x3∙x1 = 8 x1, x2, x3 ≥ 0
7. z = x12 + x22 +x3 8. z = x1∙x2 + x2∙x3
при x1+ x2+x3 2 = 4 при x1+ x2 = 4
2x1 – 3x2 = 12 x2 + x3 = 4
9. z = x1∙x2∙x3 10. z = 6 – 4x1 – 3x2
при 2x1∙x2+x2∙x3 = 12 при x12+ x2 = 1
2x1 – x2 = 8
11. z = 4x1 + x12 + 8x2 + x22 12. z = x12∙x2 + x22∙x1 + x1∙x2∙x3 + x32 →min
при x1+ x2 = 180 при x1+x2+ x3 ≤ 15
x1, x2 ≥ 0 x1, x2 , x3 ≥ 0
13. z = x1∙x2∙x3∙x4 14. z = x1∙x2∙x3
при x1+ x2 + x3 + x4 = 4 при x1+ x2 + x3 ≤ 6
x1, x2 , x3, x4 ≥ 0 x1∙x2 + x1∙x3+ x2∙x3 ≤ 8
15. z = x1∙x2 + x1∙x3 + x2∙x3 →min 16. z = x1∙x2∙x3
при x1+x2+ x3 ≤ 4 при x1+ x2 + x3 = 6
x1∙x2 + x1∙x3+ x2∙x3 = 12
17. z = x12∙x23∙ x34→max 18. z = x1 – 2x2 + 2x3→max
при x1+ x2+ x3 =18 при x12+ x22 + x32 ≤ 9
3.6. Задачи квадратичного программирования
Постановка задачи:
1. F = f(x1, x2, xn) max,
целевая функция – многочлен второго порядка.
2 .gi(x1,
x2,xn)
bi,
i
= 1, m
– ограничения линейные.
.gi(x1,
x2,xn)
bi,
i
= 1, m
– ограничения линейные.
Если ограничения имеют вид , то они приводятся к нужному виду путем домножения на –1.
3. x1, x2,xn 0.
Квадратичная функция имеет только один экстремум. Задачи квадратичного программирования решаются с помощью теории Куна-Таккера.
Алгоритм решения.
1. Составляется функция Лагранжа:
![]() (3.21)
(3.21)
где
![]() – где неопределенные множители Лагранжа.
– где неопределенные множители Лагранжа.
2. Составляются условия Куна-Таккера:
 (3.22)
(3.22)
В условиях Куна-Таккера ограничения-неравенства заменяются равенствами путем введения искусственных переменных:
 (3.23)
(3.23)
3. Данная задача решается методами линейного программирования, например, методом искусственного базиса. Особенность решения – в процессе перехода от одной симплекс-таблицы к другой должна быть, чтобы хотя бы одна переменная из ограничений (*) и (**) свободной.
Если вид целевой функции другой (min), то ограничения следует привести к виду . Тогда условия Куна-Таккера будут выглядеть следующим образом:
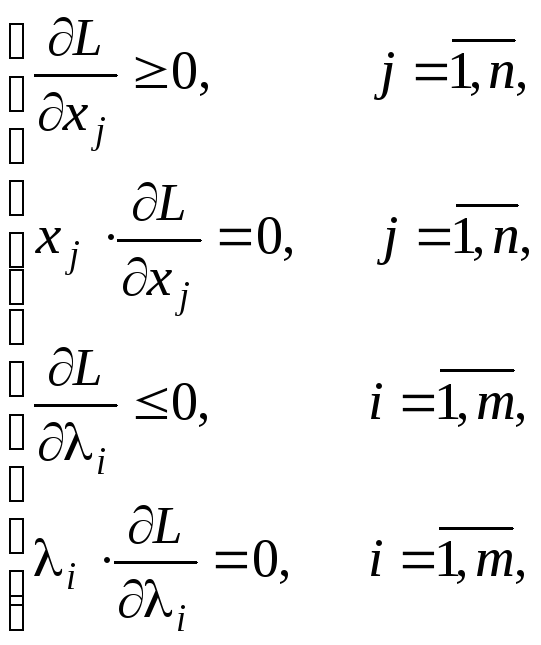 (3.24)
(3.24)
Пример.
Решить задачу квадратичного программирования

Решение.
1. Так как целевая функция минимизируется, то ограничения нужно привести к виду :

2. Составляем функцию Лагранжа:
![]()
3. Составим систему Куна-Таккера:

4. Преобразуем ограничения-неравенства в ограничения-равенства путем введения искусственных переменных:

5. Воспользуемся методом искусственного базиса для приведения задачи к каноническому виду:

Составим симплекс-таблицу:
|
|
х1 |
х2 |
1 |
2 |
v1 |
v2 |
|
|
|
w3 |
2 |
–2 |
1 |
–1 |
–1 |
0 |
2 |
|
|
w4 |
–2 |
4 |
1 |
2 |
0 |
–1 |
6 |
|
|
w1 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
|
|
w2 |
–1 |
2 |
0 |
0 |
0 |
0 |
2 |
|
|
|
0 |
–2 |
–2 |
–1 |
1 |
1 |
–8 |
|
При переходе от одной симплекс-таблицы к другой необходимо проверять выполнение ограничений-равенств. В данном случае 1 и 2 нельзя переводить из свободных в базисные.
Решение заканчивается, когда w3 = w4 = 0 и в правом нижнем углу таблицы – 0.
Ответ: х1 = 0,8, х2 = 1,2.
