5. Оптимальное управление

Оптимальное управление – это частный случай задач вариационного исчисления. Решением этих задач является оптимальная функция управления объектом [6].

5.1. Постановка задачи

Дано:

1. Объект, описывающийся системой дифференциальных уравнений в фазовых координатах:

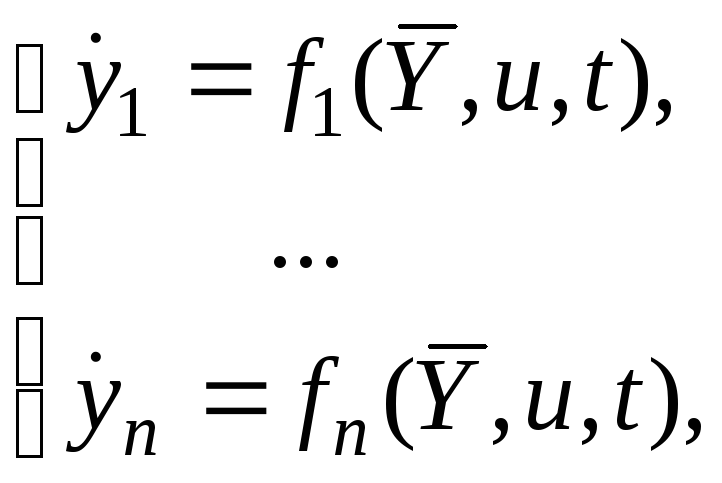(5.1)

где y_i – фазовые координаты (скорость, управление, путь), – вектор фазовых координат,– функция управления.

2. Целевая функция (обычно задается в виде определенного интеграла)

(5.2)

3. Начальные и граничные условия (всего 2n условий, n – порядок системы дифференциальных уравнений).

4. Ограничения на фазовые переменные: B_j(y₁, y₂,,y_п)  0, j = 1,,m.

5. Ограничение на управление: |u|  1, u – приведенный параметр управления.

Пример.

Лифт управляется двигателем постоянного тока. Найти такое управление, при котором лифт доходил бы с одного этажа до другого за минимальное время.

Решение.

Управление осуществляется током якоря ,  – угол поворота якоря.

, (угловая скорость), u  i, (функция управления – ток).

Система уравнений в фазовых координатах:

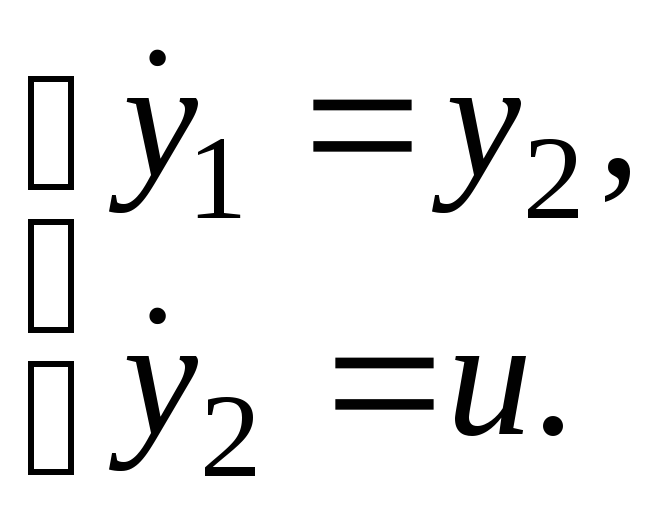
Целевая функция ,T – время управления.

Граничные условия: у₁(0) = – ₀, у₁(Т) = 0, у₂(0) = 0, у₂(Т) = 0.

|u| 1 (ток управления лежит в некотором интервале (i_min, i_max)),

₀ – угол, который должен отработать якорь двигателя.

5.2. Классификация задач оптимального управления

1. По виду целевой функции:

– задачи, оптимальные по быстродействию ,

– задачи, оптимальные по расходу энергии ,

– задачи, оптимальные по другим критериям.

2. По виду граничных условий:

– задачи с закрепленными концами (рис. 5.1), где начальное и конечное значения – точки на фазовой плоскости;

Рис. 5.1. Графическая иллюстарция задачи с закрепленными концами

– задачи с подвижными концами (рис. 5.2), где вместо точек используются какие-либо поверхности.

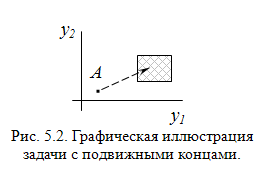
Рис. 5.2. Графическая иллюстарция задачи с закрепленными концами

На рис. 5.1 А = (у₁(0), у₂(0)) – начальная точка, В = (у₁(Т), у₂(Т)) – конечная точка. Задача заключается в нахождении такого управления, чтобы система перешла из А в В оптимальным образом (начальная точка считается левой, а конечная – правой).

Если конец подвижный, то граничные условия записываются следующим образом: у_i(0) = у_0i – координата начальной точки, φ_i(у_i(T))= 0 – конечное условие – поверхность, i = 1,,п.

5.3. Принцип максимума Понтрягина

Принцип максимума Понтрягина позволяет найти оптимальное управление объектом.

Постановка задачи та же (5.1):

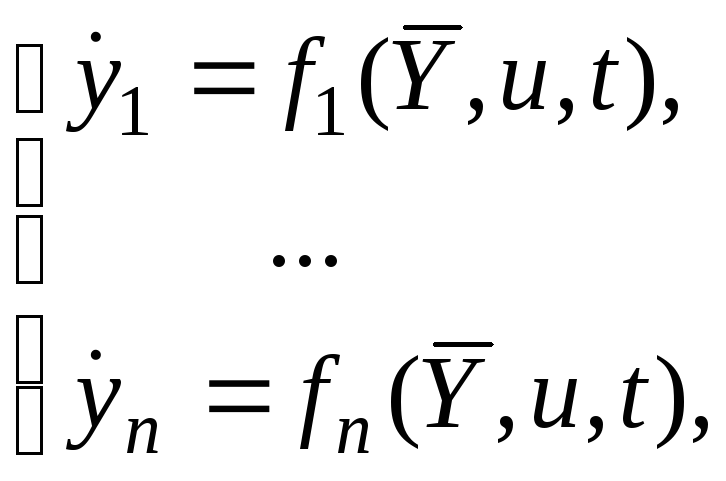
Требуется найти u(t) – функцию управления объектом.

Алгоритм принципа максимума Понтрягина

1. Введем переменную

(5.3)

Продифференцируем по времени

Добавим полученное дифференциальное уравнение к системе, описывающей объект:

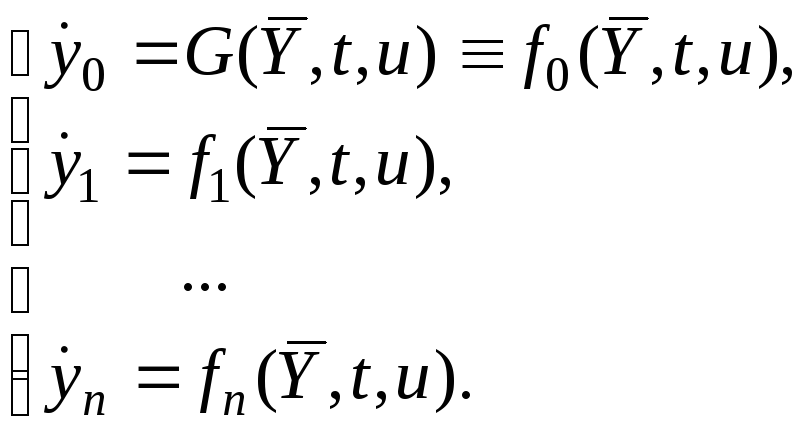(5.4)

2. Составляем функцию Гамильтона

где _i – неизвестные функции времени.

3. Находим _i из системы дифференциальных уравнений:

(5.5)

4. Найденные _i подставляем в Н.

5. Находим оптимальное управление u(t), исходя из следующего определения:

Принцип максимума Понтрягина: оптимальным является такое управление u(t), при котором функция Гамильтона достигает максимума.

6. Найденное u(t) подставляем в систему дифференциальных уравнений фазовых координат (5.4). Находим фазовые координаты как функции времени.

Пример.

Двигатель постоянного тока приводит в движение лифт. Найти такое управление лифтом, при котором лифт, переходя с одного этажа на другой, затрачивал бы минимум энергии.

Решение.

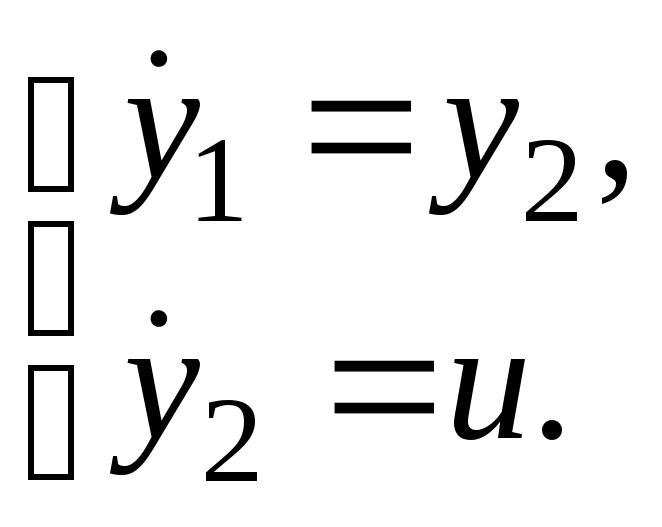
граничные условия: у₁(0) = – ₀, у₂(0) = 0, у₁(Т) = у₂(Т) = 0.

1. Составим систему дифференциальных уравнений в фазовых координатах:

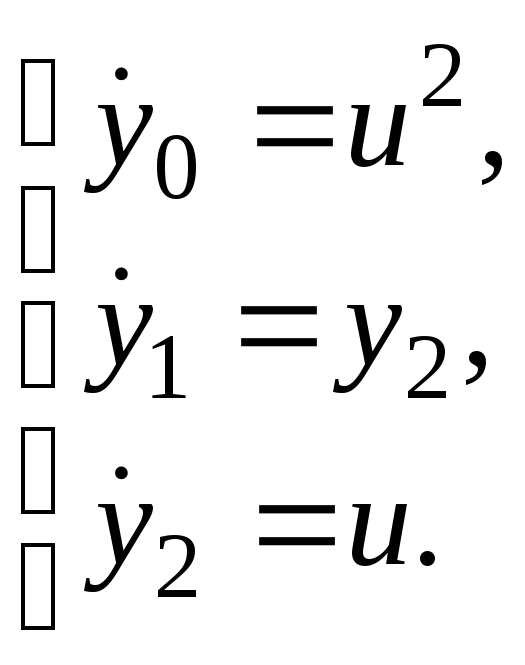
2. Запишем функцию Гамильтона:

3. Найдем функции _i из системы дифференциальных уравнений:

, следовательно, .

, , .

,

С учетом полученных _i функция Гамильтона примет вид:

4. Найдем управление, при котором функция Гамильтона достигает максимума. Для этого найдем производную и приравняем ее нулю:

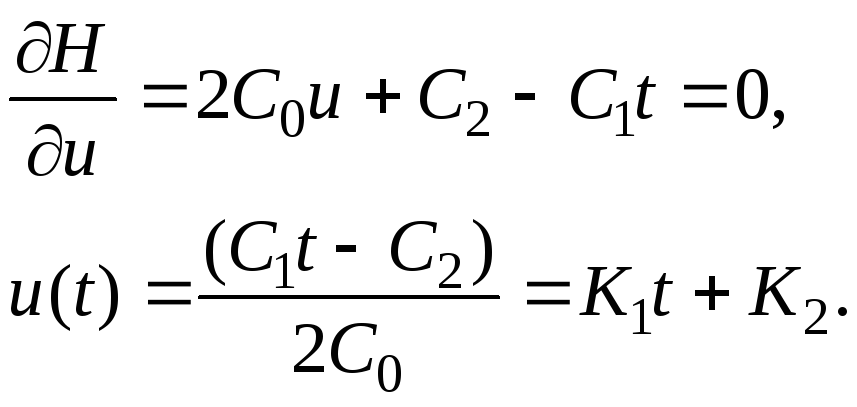
5. Подставляем найденное u(t) в систему дифференциальных уравнений в фазовых координатах:

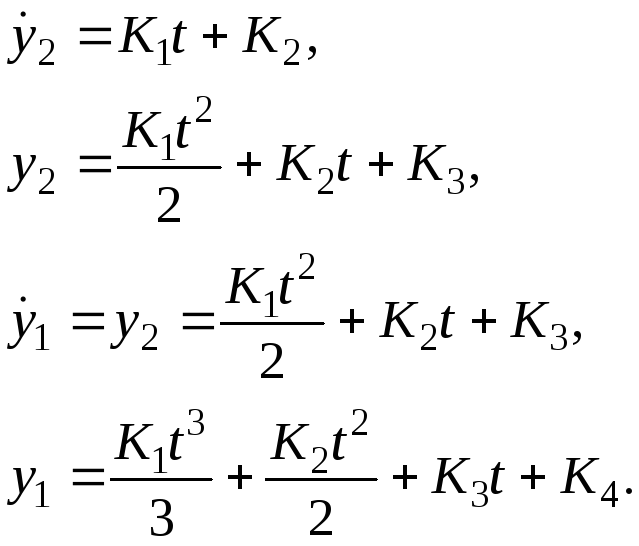
K₁,K₄ находим из граничных условий: у₁(0)= –₀, у₂(0) = 0, у₁(Т) = = у₂(Т) = 0.