
- •В.А. Панов математические основы теории систем. Методы оптимизации
- •Содержание
- •1. Основные понятия и определения 6
- •2. Линейное программирование 13
- •3. Нелинейное программирование 53
- •4. Вариационное исчисление 91
- •5. Оптимальное управление 109
- •Введение
- •1. Основные понятия и определения
- •1.1. Оптимизационная задача
- •1.2. Допустимое решение
- •1.6.1. Частные критерии
- •1.6.2. Обобщенные критерии
- •Обобщенный аддитивный критерий
- •Обобщенный мультипликативный критерий
- •1.6.3. Минимаксные критерии
- •1.7. Общая характеристика методов поиска экстремума
- •Краткая характеристика методов и задач
- •2. Линейное программирование
- •2.1. Стандартный вид задачи линейного программирования (злп)
- •2.2. Способы приведения задачи линейного программирования к стандартному виду
- •2.3. Графический метод решения задач линейного программирования
- •2.4. Симплекс-метод решения задач линейного программирования
- •2.4.1. Канонический вид злп
- •2.4.2. Симплекс-таблица, соответствующая каноническому виду
- •2.4.3. Нахождение координат вершины допустимого многогранника по каноническому виду (симплекс-таблице)
- •2.4.4. Алгоритм решения злп с помощью симплекс-метода
- •Задание для самостоятельной работы
- •2.5. Приведение злп к каноническому виду
- •2.5.1. Метод искусственного базиса
- •2.6. Алгоритм двойственного симплекс-метода
- •Задания для самостоятельной работы
- •2.7. Целочисленное линейное программирование
- •2.7.1. Метод сечения Гомори
- •2.8. Транспортная задача
- •2.8.1. Постановка задачи
- •2.8.2. Математическое описание задачи
- •2.8.3. Транспортная таблица
- •2.8.4. Таблица издержек
- •2.8.5. Метод «северо-западного» угла
- •2.8.6. Алгоритм решения транспортной задачи
- •Задания для самостоятельной работы
- •3. Нелинейное программирование
- •3.1.2.2 Метод ненаправленного поиска
- •3.1.2.3. Метод дихотомии (деление отрезка пополам)
- •3.1.2.4. Метод «золотого сечения»
- •3.1.2.5. Метод Фибоначчи
- •Задание для самостоятельного решения
- •3.2. Графический метод решения задач нелинейного программирования
- •Целевая функция линейная, ограничения нелинейны
- •Ограничения линейные, целевая функция нелинейна
- •3.3. Задачи дробно-линейного программирования
- •Задания для самостоятельного решения
- •3.4. Методы поиска безусловного экстремума функции многих переменных
- •3.4.1. Аналитический метод
- •3.4.2. Итерационные методы
- •3.4.2.1. Метод покоординатного спуска
- •3.4.2.2. Метод наискорейшего спуска
- •Задания для самостоятельной работы
- •3.5. Решение задач нелинейного программирования с ограничениями-равенствами
- •Метод неопределенных множителей Лагранжа
- •Задание для самостоятельной работы
- •3.6. Задачи квадратичного программирования
- •Задания для самостоятельной работы
- •3.7. Метод условного градиента
- •5. X1, x2,xn 0. (3.25)
- •X1, x2,xn 0.
- •Задания для самостоятельной работы
- •3.8. Метод штрафных функций
- •4. Вариационное исчисление
- •4.1. Формула Эйлера-Лагранжа
- •4.2. Частные случаи формулы Эйлера
- •4.3. Обобщенная задача вариационного исчисления
- •4.4. Решение задач вариационного исчисления с ограничениями
- •4.5. Изопериметрическая задача
- •4.6. Функционалы, зависящие от производных высших порядков
- •Задание для самостоятельного решения
- •5. Оптимальное управление
- •5.1. Постановка задачи
- •5.2. Классификация задач оптимального управления
- •5.3. Принцип максимума Понтрягина
- •5.4. Задача о максимальном быстродействии
- •Задания для самостоятельного решения
- •Список литературы
- •Основы теории оптимизации в.А. Панов
3.2. Графический метод решения задач нелинейного программирования
Этот метод применяется, когда количество переменных равно двум и либо целевая функция, либо ограничения линейные. Рассмотрим два случая.
Целевая функция линейная, ограничения нелинейны
Алгоритм решения задачи:
Ограничения-неравенства заменяем ограничениями-равенствами. Строим графики полученных функций.
Выделяем область допустимых решений.
Строим график целевой функции при каком-либо значении правой части (графиком является прямая).
График целевой функции переносим параллельно самому себе до касания с границей области допустимых решений.
Находим координаты точки касания.
Пример.
![]()
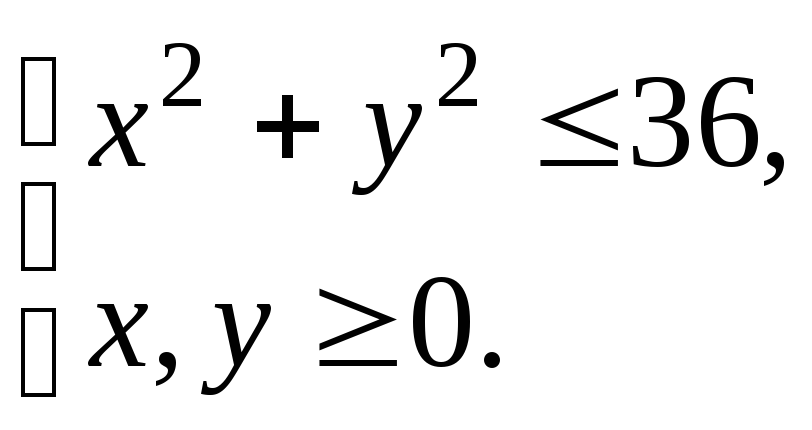
А – точка касания.
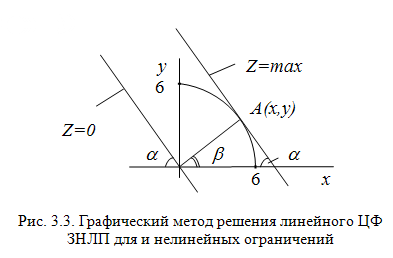
Рис. 3.4. Графический метод решения ЗНЛП для линейной ЦФ
и нелинейных ограничений
Решение.
![]()
![]()
Точка А лежит на луче, проходящим под углом к оси абсцисс. Кроме того, точка А принадлежит окружности. Следовательно, координаты точки А можно найти, решив следующую систему:
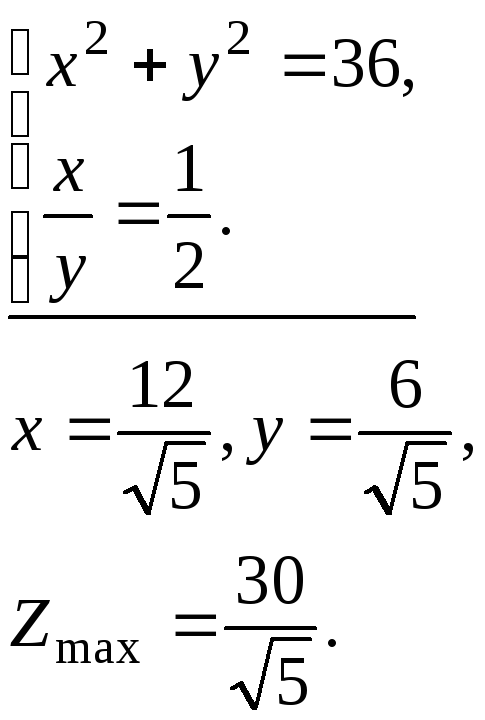 (рис.
3.4)
(рис.
3.4)
Ограничения линейные, целевая функция нелинейна
Алгоритм аналогичен предыдущему случаю с некоторыми отличиями:
область допустимых решений – выпуклый многоугольник;
для нахождения решения требуется строить семейство целевых функций.
Пример.
![]()
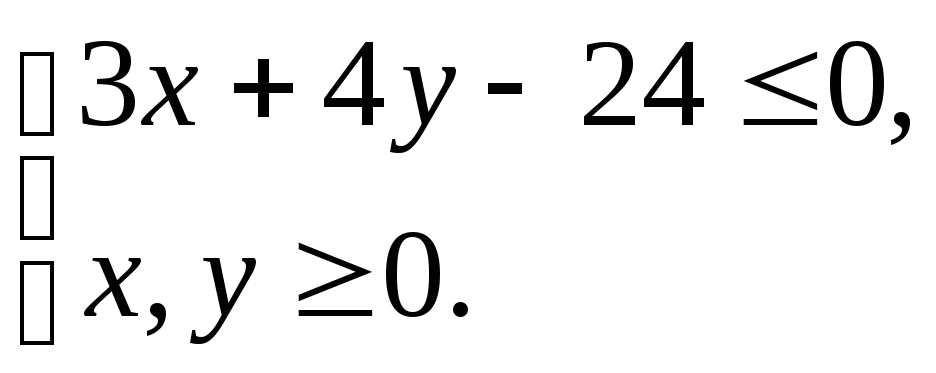
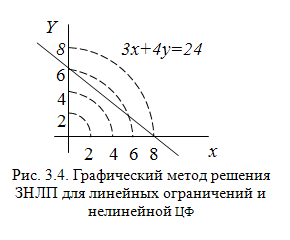
Рис. 3.5. Графический метод решения ЗНЛП
для нелинейной ЦФ и линейных ограничений
Ответ: x = 8, y = 0, Zmax = 8.
3.3. Задачи дробно-линейного программирования
Существует некоторый класс задач нелинейного программирования, который можно свести к задачам линейного программирования. Это задачи дробно-линейного программирования.
Постановка задачи:
![]() (3.6)
(3.6)
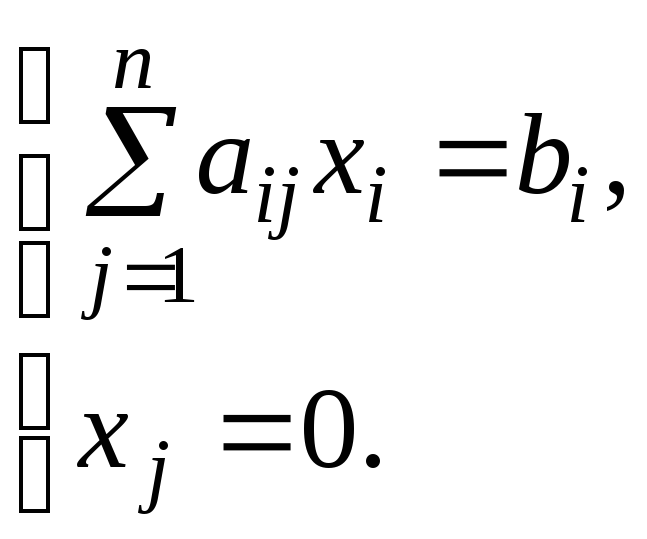
![]()
Предположим, что знаменатель целевой функции не равен нулю и положителен (если он отрицателен, то умножим числитель и знаменатель на –1).
Введем новую переменную y0:
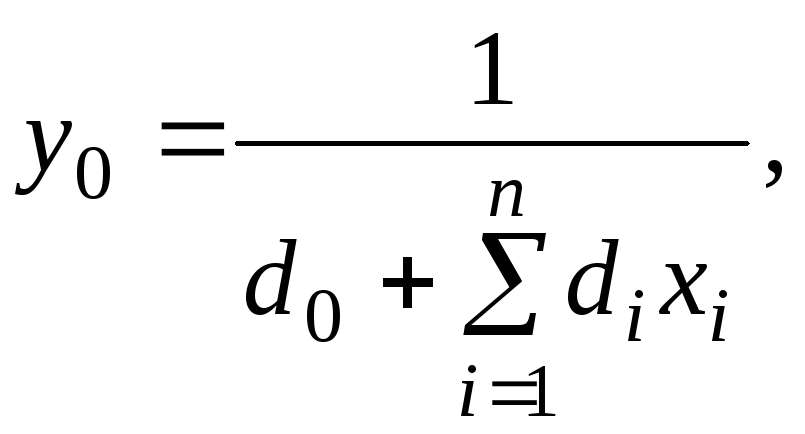 (3.7)
(3.7)
тогда ЦФ
![]() (3.8)
(3.8)
Введем
переменные
![]() ,
,![]() тогда
тогда
![]() (3.9)
(3.9)
Домножим левую и правую части ограничений на Y0:
![]()
![]() (3.10)
(3.10)
Добавим еще ограничение:
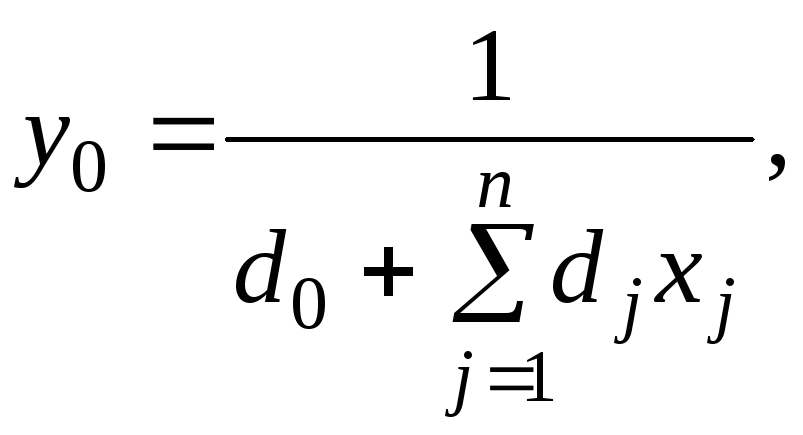
![]()
![]()
![]() (3.11)
(3.11)
Получили задачу линейного программирования ((3.9) – (3.11)). Решив ее одним из методов линейного программирования, получим оптимальное решение yj.
Далее
осуществляется переход к исходным
переменным
![]() .
.
Пример 1.
![]()
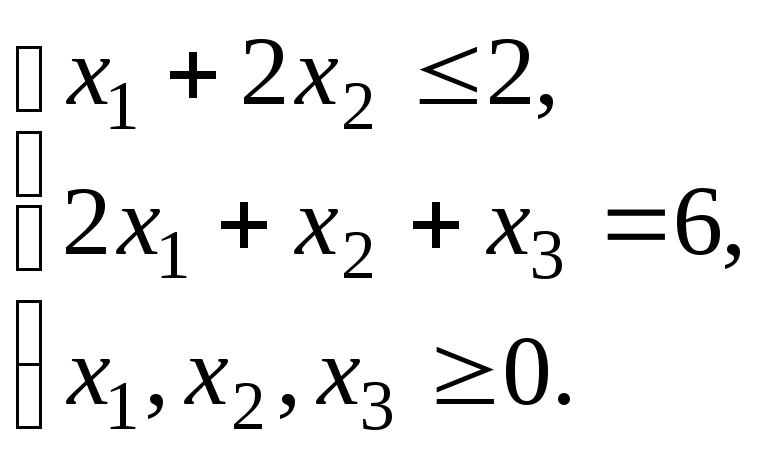
Решение.
Вводим новые переменные y0, y1, y2:
![]()
![]()
Преобразуем ограничения:
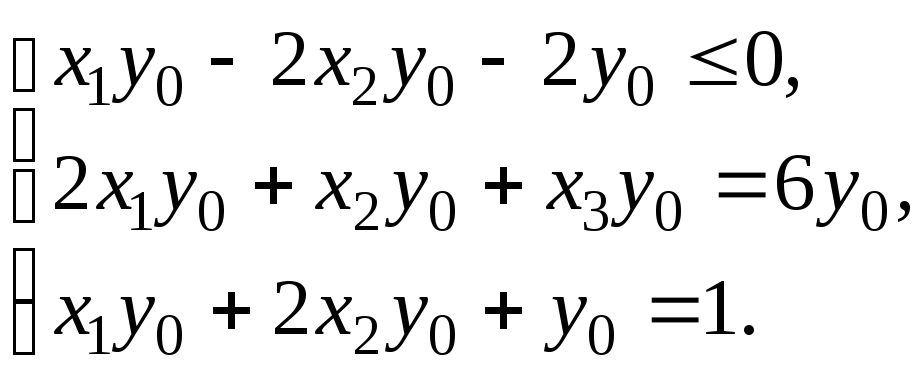
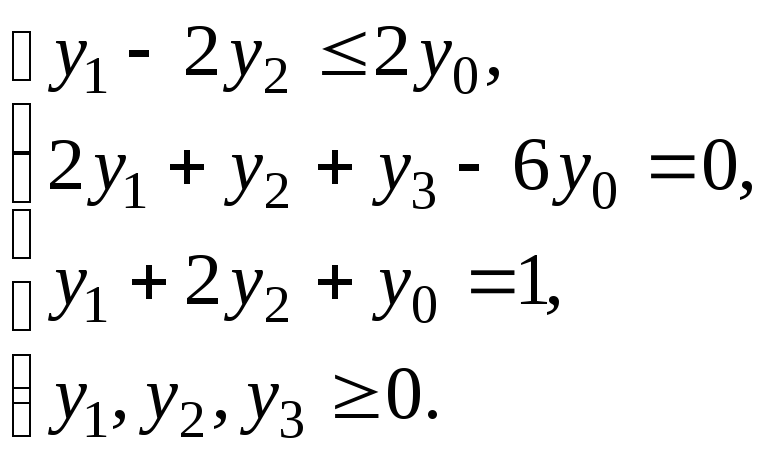
Преобразуем ограничение-неравенство в ограничение-равенство введением искусственной переменной y4:
![]()
Приведем задачу к каноническому виду методом искусственного базиса:
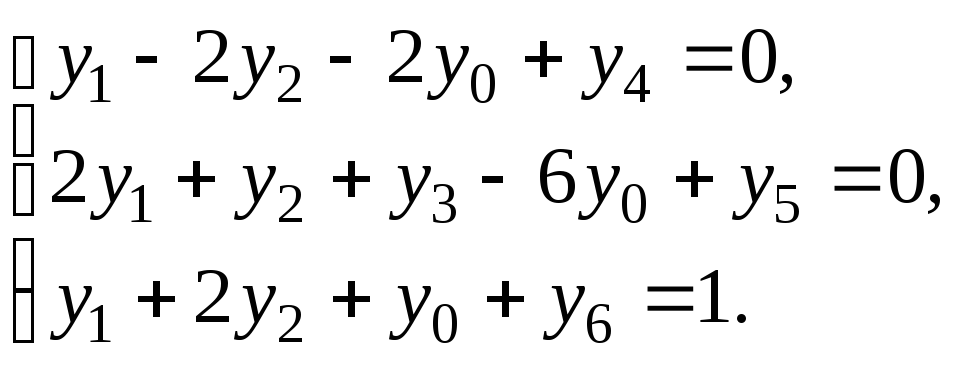
Искусственная целевая функция: G = y5 + y6 min.
В результате решения задачи методами линейного программирования получен ответ:
![]()
![]()
![]()
![]()
Переход к исходным переменным:
![]()
![]()
![]()
Пример 2.
![]()
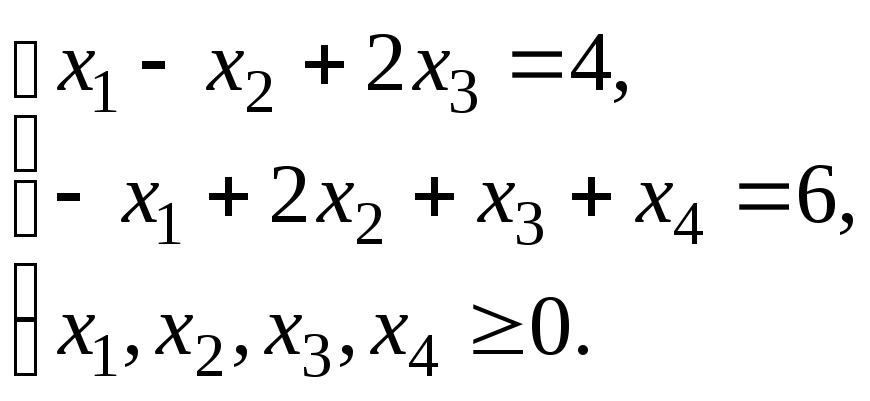
Решение.
Вводим новые переменные y0, y1, y2, y4:
![]()
![]()
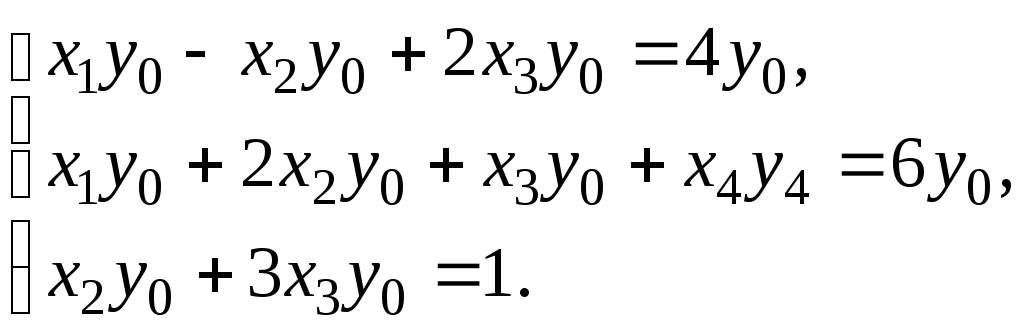
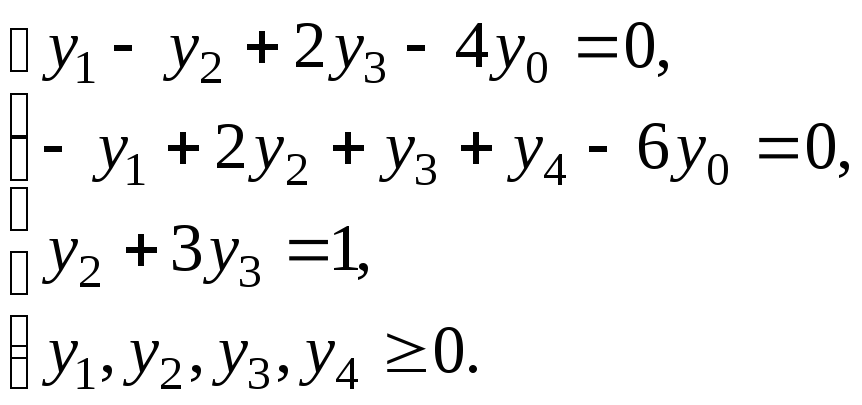
а) Искусственные переменные выражаем из ограничений и подставляем в искусственную целевую функцию:
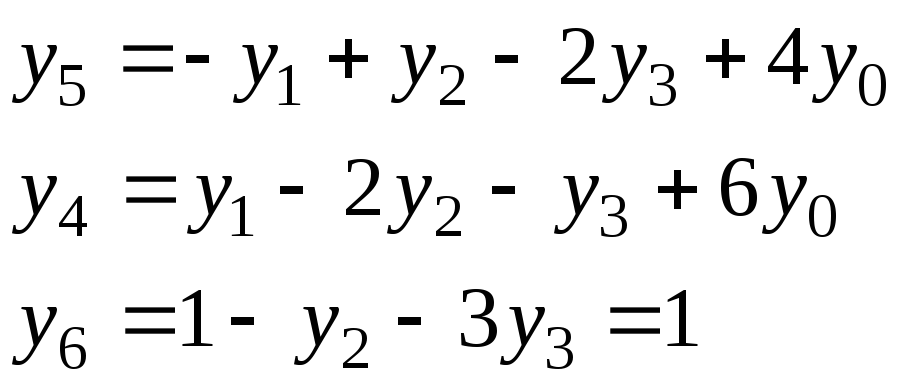
![]()
Теперь задача приведена к каноническому виду.
б) Решаем задачу линейного программирования, для которой искусственные переменные – базисные, а искомые – свободные. Задачу решаем для искусственной целевой функции.
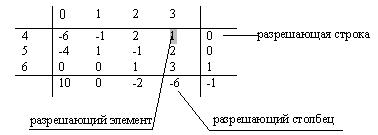
Далее по симплекс-методу выбирается разрешающий столбец (–6 – максимальный по модулю отрицательный коэффициент целевой функции), разрешающую строку (здесь разрешающей может быть любая строка, правая часть которой – 0), разрешающий элемент (1). Меняются местами переменные Y3 и Y4, причем столбец, соответствующий Y3, вычеркиваем из таблицы.
в) Новая симплекс-таблица:
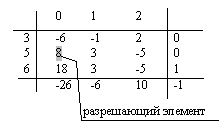
Проверяются ограничения и целевая функция:
0 – 0 + 2·0 – 4·0 + 0 = 0
0 + 2·0 + 0 + 0 – 6·0 = 0
0 + 3·0 + 1 = 1
0 + 0 + 1 = 1
Меняются местами переменные Y0 и Y5, причем столбец, соответствующий Y0, вычеркиваем из таблицы.
г) Новая симплекс-таблица:

Проверяются ограничения и целевая функция:
0 – 0 + 2·3 – 4·0 + 0 = 0
0 + 0 + 0 + 0 – 6·0 = 0
0 + 3·0 + 1 = 1
0 + 0 + 1 = 1
Меняются местами переменные y2 и y6, причем столбец, соответствующий y2, вычеркиваем из таблицы.
д) Новая симплекс-таблица:

Проверяются ограничения и целевая функция:
![]()
![]()
![]()
![]()
Как видно из таблицы, в результате тождественного преобразования исходные переменные делятся на базисные и свободные.
е) Переход к исходной целевой функции:
Q = 3Y2 – 2Y3
Записываются ограничения, полученные из итоговой симплекс-таблицы:
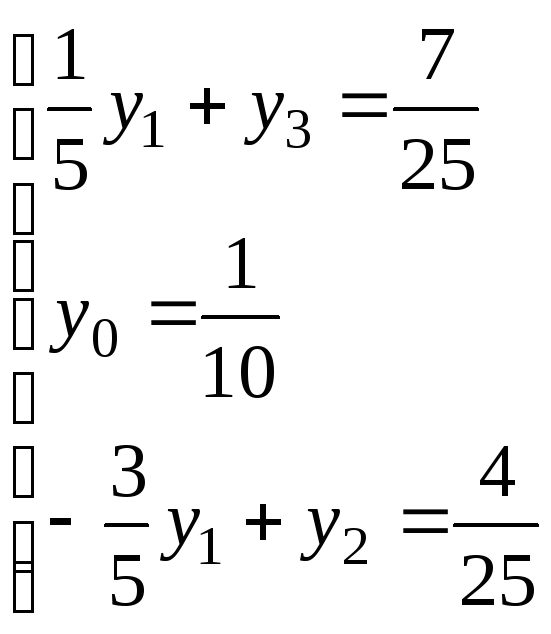
Выразим базисные переменные через свободные и подставим эти выражения в целевую функцию:
![]()
В итоге получена начальная симплекс-таблица, т.е. задача приведена к каноническому виду.
|
|
1 |
|
|
0 |
0 |
1/10 |
|
2 |
–3/5 |
4/25 |
|
3 |
1/5 |
7/25 |
|
|
7/5 |
2/25 |
Как видим, все коэффициенты целевой функции положительны, следовательно, решение оптимальное.
![]()
![]()
![]()
![]()
Переход к исходным переменным:
![]()
![]()
![]()
![]()
Задача приводится к каноническому виду методом искусственного базиса:
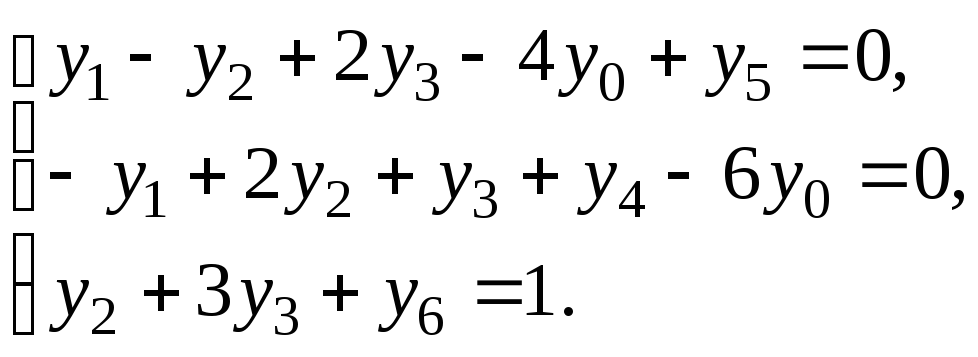
Искусственная целевая функция: G = y4 + y5 + y6 min.
