§ 26. Клика

Антиподом понятия независимого множества является понятие клики. Подмножество V вершин графа G называется кликой, если любые две входящие в него вершины смежны, т. е. если порожденный подграф G(V') является полным. Клика называется максимальной, если она не содержится в клике с большим числом вершин, и наибольшей, если число вершин в ней наибольшее среди всех клик. Число вершин в наибольшей клике графа G называется его плотностью (или кликовым числом) и обозначается через φ(G). Как и в случае независимых множеств, максимальная клика графа может оказаться не наибольшей, и это обстоятельство делает задачи нахождения числа φ (G) и наибольшей клики для произвольного графа G крайне трудными. Очевидно следующее

Утверждение 26.1. Подмножество вершин графа G является кликой тогда и только тогда, когда оно независимо в дополнительном графе G. Следовательно, φ(G) = a₀ (G).

С помощью этого утверждения и приведенных в § 25 оценок числа а0(G) просто получаются соответствующие оценки числа φ(G).

Очевидно, что все клики графа, как и все максимальные клики, составляют покрытие множества вершин.Н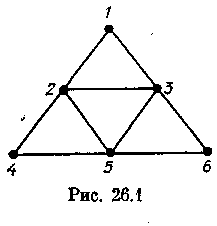аименьшее число клик графаG, покрывающих множество VG, называется числом кликового покрытия и обозначается через c(G).

Очевидно, что c(G)>=a₀ (G) для любого графа G.

О взаимном расположении клик в графе можно судить по свойствам вводимого ниже графа клик.

Граф пересечений максимальных клик графа G назовем графом клик и обозначим через Q(G). Таким образом, вершины графа Q(G) объективно соответствуют максимальным кликам графа G и две вершины смежны тогда и только тогда, когда соответствующие клики пересекаются. Если для некоторого графа H существует такой граф G, что H=Q(G), то Н также называется графом клик.

Очевидно, что граф Q(G) может быть как «большим», так и «малым». Например, Q(0_n) = 0_n, Q(K_n) = K₁, Q(K_1,n)=K_n, Q(P_n)=P_n-1 Q(C_n) = C_n. Для графа G, изображенного на рис. 26.1, Q(G) = K₄.

Известно, что существуют графы, не являющиеся графами клик. Таков, например, граф, представленный на рис. 26.1. Тем не менее следующая теорема свидетельствует о том, что расположение клик в произвольном графе достаточно произвольно.

Теорема 26.2. Для любого (n, m)-графа Н существует такой граф G порядка

n + m, что Н изоморфен некоторому порожденному подграфу графа клик Q(G). Если при этом H не содержит треугольников, то граф G можно выбрать так, что H=Q(G).

Пусть

Описанным ниже способом построим графG с множеством вершин

Если

-множество всех ребер графа Н, инцидентных вершине i, то положим

- полный граф с множеством вершин V_i,

Рассмотрим граф клик Q(G). Очевидно, что каждое из множеств V_i служит максимальной кликой графа G. Кроме этого, возможны еще максимальные клики, не содержащие вершин вида vi. Пусть X — одна из них,

Заметим, чтоE_aE_в EG тогда и только тогда, когда ребра е_а и е_В графа G смежны. Поэтому из (1) следует, что существует вершина k, инцидентная

каждому из ребер е_а и е_В, и потому Е_а  V_k,, E_В V_k. Таким образом, |Х| > 2 и любые две вершины, принадлежащие клике X, вместе входят в какое-либо из множеств V_i. Поскольку клика X не совпадает ни с одним из V_i, то в ней есть три вершины Е_а, Е_В, E_γ такие, что Е_а,, Е_В  V_k,, Е_а, E _γ Vi, E _γ Vj и индексы i,j, k попарно различны. Тогда ребра e_a, е_В, е _γ составляют в графе Н треугольник (рис. 26.2). Поскольку в графе Н нет четвертого ребра, смежного с каждым из ребер е_а, е_В, е _γ, то |Х| =3, X = Х_{аВ γ} = {Е_а, E_В, E_γ.}

Очевидно и обратное: если ребра е_a,, е_b е_γ составляют треугольник в графе Н, то множество Х _{α β γ} является максимальной кликой графа G.

Таким образом, если в H нет треугольников, то VQ(G) = {V₁, V₂, ..., V_n}. Если в графе Н есть треугольники, то вершинами графа Q(G) служат все множества Vi и все клики графа G вида Х _{α β γ}

В любой ситуации обозначим через F подграф графа Q(G], порожденный множеством вершин V = {V1 V2, ... ..., Vn). Очевидно, что отображение УН ->V, при котором i -> Vi, является изоморфизмом графов Н и F. Итак, если в Н нет треугольников, то H=Q(G). В противном случае граф Н изоморфен порожденному подграфу F графа Q(G)

На рис. 26.3 изображен граф G, описанный в доказательстве предыдущей теоремы; в качестве Н взят граф,

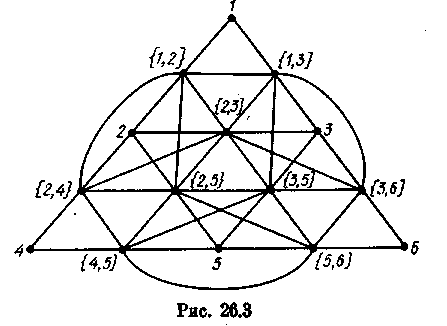
представленный на рис. 26.1, а на рис. 26.4 показан граф клик Q(G).

Следствие 26.3. Всякий граф, не содержащий треугольников, является графом клик.

Иногда полезно понятие матрицы клик. Пусть G — произвольный граф, Q = {Q₁, Q₂, ..., Q_n] — множество всех его максимальных клик, VG ={v₁, v₂, ..., v_n}. Следующим образом определим бинарную p*n-матрицу С => = C(G), строки которой соответствуют кликам из множества Q, а столбцы — вершинам графа G:

Матрица С (G) называется матрицей клик графа G.

Очевидно, что матрица клик определяется с точностью до перестановок строк и столбцов.

Например, для графа G, изображенного на рис. 26.1,