Глава IV Независимость и покрытия

Во многих прикладных задачах требуется найти в конечном множестве объектов максимальную систему объектов, попарно не связанных друг с другом, или же выбрать минимальную систему объектов, связанных со всеми другими. Формулировки подобных задач на языке теории графов приводят к понятиям независимости и покрытия.

§ 25. Независимые множества и покрытия

Множество вершин графа называется независимым (или внутренне устойчивым), если никакие две вершины из этого множества не смежны. Иными словами, если S  VG и S независимо в графе G, то порожденный подграф G(S) является пустым. Очевидно, что если при этом S'  S, то S' — также независимое множество.

Независимое множество называется максимальным, если оно не является собственным подмножеством некоторого другого независимого множества. Наибольшее по мощности независимое множество называется наибольшим. Ясно, что наибольшее независимое множество является максимальным. Обратное, вообще говоря, неверно.

К отысканию наибольшего независимого множества вершин в графе сводится, например, известная задача о восьми ферзях, которую связывают с именем К. Гаусса.

Задача о восьми ферзях: требуется так расставить на шахматной доске наибольшее число ферзей, чтобы они не атаковали друг друга.

Таких ферзей, очевидно, может быть не более восьми, так как никакие два из них не должны находиться на одной вертикали или горизонтали. Рассмотрим граф, вершины которого соответствуют клеткам доски, а ребра — парам клеток, лежащих на одной вертикали, горизонтали или диагонали. Ясно, что требуемой в задаче расстановке ферзей соответствует наибольшее независимое множество в этом графе. Одно из решений задачи о восьми ферзях показано на рис. 25.1.

Число вершин в наибольшем независимом множестве графа G называется числом независимости (числом внутренней устойчивости, неплотностью) этого графа и обозначается через a₀(G).

Н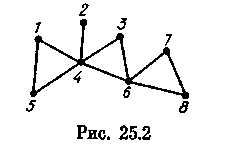апример, для графа G, изображенного на рис.25.2,a₀(G) = 4, множества вершин {1, 2, 3, 7}, {1, 2, 3, 8}, {2, 3, 5, 7} и {2, 3, 5, 8} являются наибольшими независимыми, а {4, 7} — максимальное независимое множество, не являющееся наибольшим.

Содержанием большинства задач, связанных с понятием независимости, являются определение числа независимости и отыскание наибольшего независимого множества. Эти задачи, как правило, очень трудны, и потому для их решения оказываются полезными оценки числа независимости.

Теорема 25.1. Для любого графа G верно неравенство

► Если G — полный граф, то в (1) имеет место равенство. Поэтому, не теряя общности, будем считать, что GK_n.

Воспользуемся индукцией по числу вершин графаG. В справедливости неравенства (1) для графов порядка n2 легко убедиться непосредственно. Пусть теперь |VG| = n > 2 и для всех графов порядка, меньшего чем n, неравенство (1) верно. Выберем в графе G вершину х минимальной степени. Так как GК_n, то x U N(x)  VG. Пусть G' = G — (x U N(x)). Согласно индуктивному предположению для графа G' верно неравенство, аналогичное неравенству (1). Пусть М' — наибольшее независимое множество вершин графа

G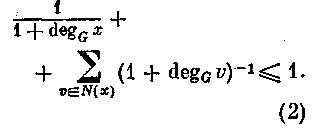'.Ясно, что множество М = М' U х независимо в графе G, и для доказательства теоремы достаточно показать, что S₁ = (1 + deg_G v)^-1  S₂ = v є VG' (1 + deg_G' v) ^-1+1. Обозначим через Q множество вершин графа G', каждая из которых смежна в G с какой-либо вершиной из N(x) (см. рис. 25.3). Очевидно, что слагаемые в S1, соответствующие вершинам v из О. меньше аналогичных слагаемых в S2, а слагаемые в S1 и S2, соответствующие вершинам v из VG' \Q , совпадают. Стало быть, достаточно показать, что

Согласно выбору вершины х для любой вершины у из N (х) имеем deg_G х  deg_G у.

Поэтому левая часть неравенства (2) является суммой (l + deg_G x) слагаемых, не превосходящих (l + deg_Gx)^-1 и, следовательно, не превосходит 1. ◄ Пусть

• среднее арифметическое степеней графа G.

Следствие25.2. Для любого графа G порядка n верно неравенство Известно неравенство Коши — Буняковского

для любых а_i, b_i >=0. Полагая

получим

По существу, доказательство теоремы 25.1 дает простой алгоритм построения независимого множества М такого, что

Это множество строится следующим образом: каждый раз в графе выбирается вершина минимальной степени и заносится в множество М. Затем эта вершина и все смежные с ней удаляются из графа и процесс продолжается. Как уже отмечалось, задача отыскания наибольшего независимого множества вершин в графе очень трудна для алгоритмического решения. Поэтому множество М, построенное описанным выше способом, иногда принимают в качестве ее приближенного решения. Что можно сказать о точности такого решения, или, иначе говоря, как далеко величина  v VG (1 + deg v)^-1 может отстоять от

а₀(G)? Ниже показано, что отношение первой из этих величин ко второй может быть сколь угодно малым числом, т.е. такое решение может оказаться плохим.

Рассмотрим граф G — G_m, для которого множества V₁, v₂, v₃ ,{u}, {v} образуют разбиение VG, |Vi|=m (i = 1,З), EG= U (i є 1) Ei, E_l = {vx:x є V₁}, E₂ = (xy:

x є V₁, y єV₂}, E₃ = (xy: x є V₂, y єV₃}, Е₄ = {их: x єV₁ пересечение с V₃}, E₅ = {xy: x є V₂, у є V₂, х ¢ у} (см. рис. 25.4, где изображен граф G₄). Легко видеть, что при любом m≥2 верно равенство a₀(G_m) = 2m. В то же время мощность множества М в графе G_m равна трем.

Пусть снова G — произвольный граф, δ =δ(G) — максимум степеней его вершин. Тогда из теоремы 25.1 очевидно следует неравенство

которое, впрочем, нетрудно получить непосредственно.Теорема Брукса (см. § 54) дает более точную оценку: если G — связный граф, , δ = δ(G) ≥ 3 и G К_п, то

э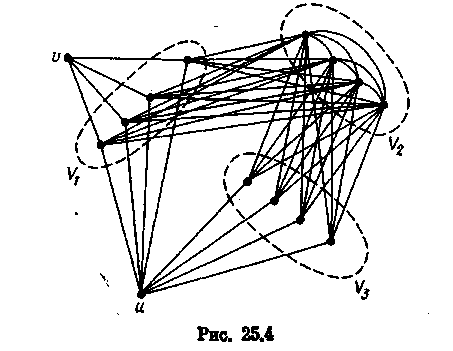та оценка предпочтительнее оценки(1) в случае, когда граф G — регулярный или близкий к регулярному. Так,

если G — кубический граф, то из неравенства (4) получаем ao(G)≥ n/3, в то время как (1) дает только а₀(G) ≥ n/4. Легко, однако, привести примеры, в которых более точна оценка (1).

Дальнейшее уточнение нижней оценки числа a₀(G) связано с использованием, помимо степенной последовательности, дополнительной информации о графе и сужением класса рассматриваемых графов. Следующая теорема, приводимая без доказательства, усиливает оценки (1) и (3) для рассматриваемых в ней классов графов.

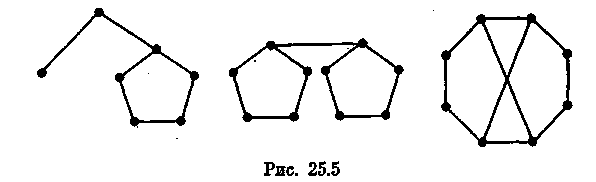
Теорема 25.3 (Д. Григгс, 1983 г.). Пусть G — связный граф порядка n≥3, не содержащий треугольников и не являющийся цепью либо циклом нечетной длины. Тогда

Приведенное неравенство превращается в равенство тогда и только тогда, когда граф G является циклом четной длины или совпадает с одним из графов, изображенных на рис. 25.5.

Независимое множество вершин графа имеет естественную матричную интерпретацию. Пусть X = {v₁, v₂, ... ..., v_k} — независимое множество вершин графа G, A = = A(G)—матрица смежности. Множеству X в матрице А соответствует подматрица, элементы которой, расположенные в строках и столбцах, соответствующих элементам

множества X, равны нулю. Такое представление позволяет получить верхнюю оценку числа a₀(G) с помощью характеристических чисел матрицы А.

Обозначим через p⁺, р^- и р° число положительных, отрицательных и нулевых собственных значений матрицы смежности графа соответственно.

Теорема 25.4 (Д. Цветкович, 1973 г.). Для всякого графа G справедливо неравенство

►Пусть a₀(G) = m. В графе G есть порожденный пустой подграф порядка т. При подходящей нумерации вершин этому подграфу соответствует подматрица А' матрицы А, занимающая строки и столбцы с номерами 1, 2, ..., m, все элементы которой равны нулю. Пусть λ1, λ2 ≥…. ≥ λn, μ1 ≥μ2…..≥. μn. Эти числа связаны известными неравенствами Коши см. [23]. Поскольку А' — нулевая матрица, то все μi = 0. Отсюда получаем неравенства

Из этих неравенств следует, что р⁺ + р°≥ mи р^- + р° ≥ т, . е. m  р° + min {р^-, р⁺}. Неравенство (6) доказано. Независимые множества вершин графа имеют самые разнообразные применения. Оставляя в стороне головоломки и задачи развлекательного характера, рассмотрим одно из применений независимости в теории информации. Возникающую здесь ситуацию можно упрощенно описать следующим образом. Источник информации посылает сообщения, являющиеся последовательностями сигналов из множества Х=(x₁,x₂,..,x_m}. При передаче возникают (например, вследствие помех) искажения сигналов. Поэтому на принимающей станции некоторые сигналы могут быть поняты как другие, т. е. перепутаны. Рассмотрим граф G, у которого VG = X и XiXj  EG, если и только если xi и хj могут быть перепутаны. Тогда, чтобы получить безошибочный код, т. е. исключить перепутывания, следует пользоваться сигналами из независимого подмножества вершин графа G. Стремление получить максимальное количество таких сигналов приводит к задаче отыскания наибольшего независимого множества вершин в графе G.

Обычно одним сигналом не ограничиваются, а посылают тексты в виде слов. Если все передаваемые слова имеют длину k, то очевидно, что рассматриваемый код содержит по меньшей мере (ao(G))^k слов, различаемых при приеме. Но фактически их может быть больше. Рассмотрим пример, принадлежащий К. Шеннону. Пусть G = Cs — простой цикл длины 5 с вершинами, пронумерованными числами 1, 2, ..., 5 в порядке следования по циклу. Тогда a₀(G) = 2, {1, 3} — наибольшее независимое множество вершин графа G. Это множество дает 4 слова (1, 1), (1, 3), (3, 1), (3, 3) длины 2, которые различимы, т. е. при приеме не может быть приняты одно в качестве другого

т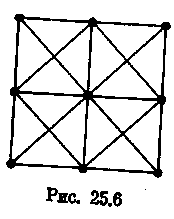акже различимы. Максимальное число различимых слов удобно описывается с помощью вводимых ниже терминов. Пусть G - произвольный граф, к - натуральное число. Следующим образом определим граф G^k - сильную степень

графа G. Множество вершин графа G совпадает с декартовой степенью (VG)^k; несовпадающие вершины (u₁, u₂,..., u_k) и (v₁, v₂,..., v_k) смежны в графе G^k тогда и только тогда, когда для каждого индекса i = = 1, k выполняется условие u1 = v₁ или u1v1 принадлежит EG. На рис. 25.6 изображен граф G₂, где G — P₃.

Очевидно, что если графу G придается тот же смысл, что и в описанной выше задаче из теории информации, то наибольшее число различимых слов длины k равно числу независимости a₀ (G^k). Очевидно также, что

a₀ (G^k)>=>(a₀ (G))^k