Emelichev_V_A_Melnikov_O_I_Sarvanov_V_I_T / Глава VII

Глава VII

^Обходы

Основные положения этой главы связаны с существо­ванием в графе эйлеровых или гамильтоновых цепей и циклов. Подобные вопросы возникли в значительной ме­ре под влиянием головоломок и игр. Тем не менее зада­чи, касающиеся эйлеровых и, в особенности, гамильтоно­вых цепей и циклов, чрезвычайно часто встречаются на практике. Это случается, например, в ситуациях, когда качество выполнения некоторого комплекса операций (работ, мероприятий) существенно зависит от порядка, в котором они выполняются.

§ 43. Эйлеровы графы

Все сказанное в этом параграфе о графах в равной степени относится к мультиграфам.

Начало теории графов как раздела математики связы­вают с так называемой задачей о кёнигсбергских мостах. Эта знаменитая в свое время задача состоит в следующем. Семь мостов города Кенигсберга (ныне Калининград) были расположены на реке Прегель так, как изображено

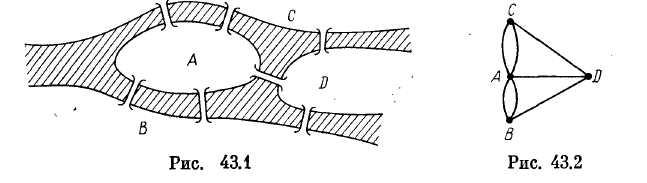
на рис. 43.1. Спрашивается, можно ли, выйдя из дома, вернуться обратно, пройдя в точности один раз по каж­дому мосту?

Сопоставим плану города граф G, вершины которого соответствуют четырем разделяемым рекой участкам су­ши Л, В, С и D, а ребра — мостам. Этот граф (точнее, мультиграф) изображен на рис. 43.2. Таким образом, задачу о кёнигсбергских мостах можно на языке теории графов сформулировать так: есть ли в мультиграфе G цикл, содержащий все ребра этого мультиграфа?

Эйлер доказал неразрешимость задачи о кёнигсберг­ских мостах. В своей работе, опубликованной в 1736 году, он сформулировал и решил следующую общую проблему

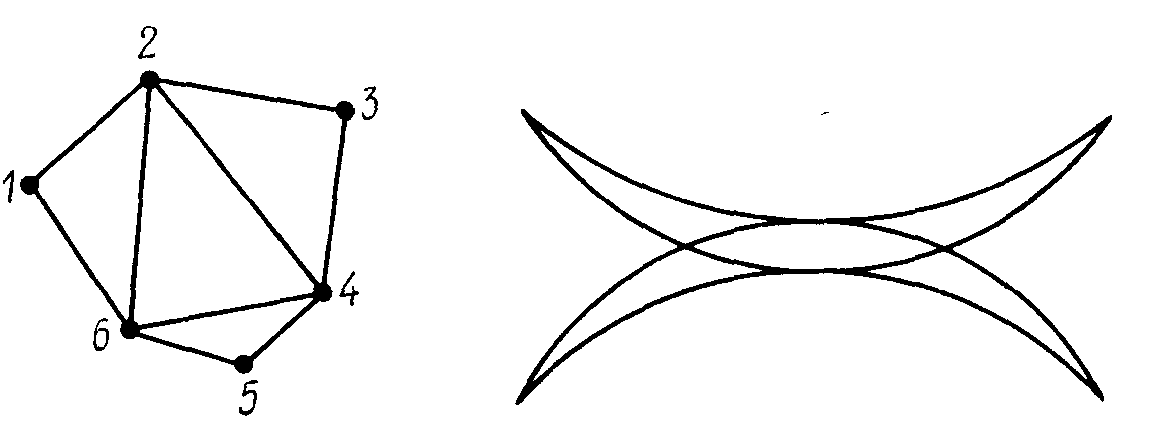
рис 43.3 рис.43.4

теории графов: при каких условиях связный граф содер­жит цикл, проходящий через каждое его ребро?

Цикл в графе называется эйлеровым, если он содер­жит все ребра графа. Связный граф, в котором есть эйле­ров цикл, называется эйлеровым графом. Такой граф мож-но нарисовать, не отрывая карандаша от бумаги и не повторяя линий.

Например, граф, изображенный на рис. 43.3, является эйлеровым, поскольку он содержит эйлеров цикл (1, 2, 3, 4, 5, 6, 4, 2, 6, 1). В этом графе есть и другие эйлеровы циклы. Ясно, что любые два таких цикла отличаются друг от друга только порядком обхода ребер.

Помимо задачи о кёнигсбергских мостах известен ряд других старинных занимательных задач (головоломок), решение которых сводится к выяснению вопроса «являет­ся ли граф эйлеровым?». В одной из них требуется обри­совать фигуру, именуемую саблями (знаком) Магомета (рис. 43.4), не отрывая карандаша от бумаги и не повто­ряя линий.

Теорема 43.1 (Л. Эйлер, 1736 г.). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.

Необходимость. Пусть G - эйлеров граф. Эйлеров цикл этого графа, проходя через каждую его верши-ну, входит в нее по одному ребру, а выходит по другому. Это означает, что каждая вершина инцидентна четному числу ребер эйлерова цикла, а поскольку такой цикл со­держит все ребра графа G, то отсюда следует четность степеней всех его вершин.

Д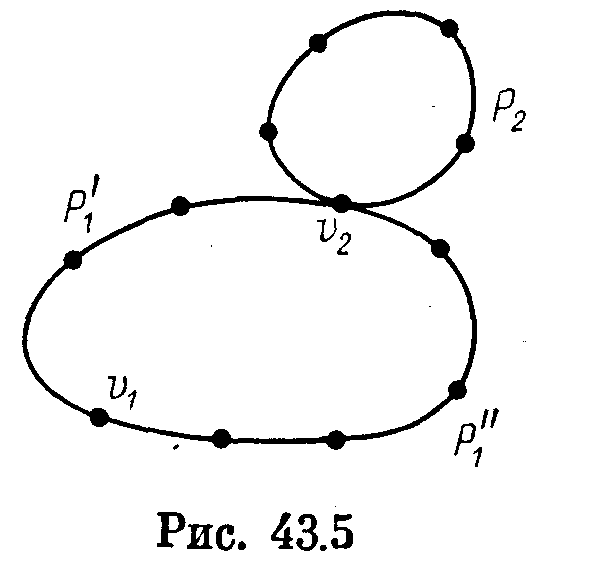остаточность. Предположим теперь, что степени вершин графа G четны. Начнем цепь P₁ из произвольной вершины v₁ и будем продолжать ее, насколько возможно, выбирая каждый раз новое ребро. Так как степени всех вершин четны, то попав в очередную отличную от v₁ вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Поэтому цепь P₁ можно продолжить путем добавления этого ребра. Таким образом, построение цепи P₁ закончится в вершине v₁, т. е. P₁ непременно бу­дет циклом. Если окажется, что P₁ содержит все ребра графа G, то это будет требуемый эйлеров цикл. В про­тивном случае, удалив из G все ребра цикла P₁, рассмот­рим граф G₁, полученный в результате такой операции. Поскольку P₁ и G имели вершины только четных степе­ней, то, очевидно, и G₁ будет обладать тем же свойством. Кроме того, в силу связности графа G графы P₁ и G₁ должны иметь хотя бы одну общую вершину v₂. Теперь, начиная с вершины v₂, построим цикл P₂ в графе G₁ по­добно тому, как строили цикл P₁. Обозначим через P’₁ и P’’₁ части цикла P₁ от v₁ до v₂ и от v₂ до v₁ соответст­венно. Получим новый цикл

P₁

который, начиная с V\, проходит по ребрам цепи Pi до V2, затем обходит все ребра цикла Рг и, наконец, возвра­щается в v\ по ребрам цепи Р[ (рис. 43.5).

Если цикл Рз не эйлеров, то проделав аналогичные по­строения, получим еще большой цикл и т. д. Этот процесс закончится построением эйлерова цикла. '<

Будем говорить, что набор ребер-но непересекающихся цепей (не обя­зательно простых) покрывает граф G, если каждое ребро графа G входит в одну из этих цепей. Пусть связный граф G содержит к вершин нечетной степени. По лемме о рукопожатиях к четно. Рассмотрим граф G', полу­ченный добавлением к G новой вер­шины v и ребер, соединяющих v с вершинами графа G нечетной степени. Поскольку степени всех вершин графа G' четны, то G' содержит эйлеров цикл. Если теперь выбросить v из этого цикла, то получится к/2 цепей, со­держащих все ребра графа G, т. е. покрывающих G.

С другой стороны, граф, являющийся объединением r ре-ерно-непересекающихся цепей, имеет самое большее 2r вершин нечетной степени. Поэтому меньшим числом це-пей граф G покрыть нельзя. Тем самым доказано

Следствие 43.2. Если связный граф содержит ров-но k вершин нечетной степени, то минимальное число покрывающих его реберно-непересекающихся цепей рано k/2.

В частности, когда к = 2, граф имеет цепь, которая соединяет вершины нечетной степени и содержит все ребра графа. Цепь, содержащую все ребра. графа, называют эйлеровой.

Из доказательства теоремы 43.1 видно, что эйлеров граф содержит, как правило, несколько эйлеровых циклов. Зная один такой цикл, получить новый можно сле-дующим простым приемом.

Пусть С — исходный эйлеров цикл, и вершина и проводится в этом цикле более одного раза. Рассмотрим часть (подцикл) цикла С, состоящую, из ребер и вершин, проходимых между k-м и l-м (к < l) посещениями вершины v. Это будет некоторый цикл С\. Цикл С, как и всякий эйлеров цикл, задает некоторый порядок обхода ребер графа и индуцирует порядок прохождения ребер цикла С\ .Если теперь порядок обхода ребер С\ изменить на обратный, а на остальных ребрах оставить его таким, каким он был в С, то, очевидно, получим новый эйлеров цикл С' . Например, в графе, изображенном на рис. 43.3, можно получить новый цикл С' = (1, 2, 6, 5, 4, 3, 2, 4, 6,1), полагая C=(1,2,3,4,5,6,2,4,6,1) и С\ = (2, 3, 4, 5, 6, 2).

В этом примере цикл С\ составлен из ребер, проходимых С между первым и вторым посещениями вершины 2.

Итак, изменив указанным способом эйлеров цикл, по­лучаем новый эйлеров цикл. Следующая теорема, приводимая здесь без доказательства, утверждает, что последовательности таких изменений достаточно для получения всех эйлеровых циклов из данного.

Теорема 43.3 (А. Коциг, 1980 г.). Если С и С' —Элеровы циклы графа G, то в G существует такая последователъностъ эйлеровых циклов С = С\,Сг,...,С_к=С', что C_i+i получается из С г путем изменения порядка обxoдa ребер некоторого подцикла на обратный.

Естественно возникает вопрос: как найти хотя бы один эйлеров цикл в эйлеровом графе G, т. е. как зану-меровать ребра графа числами 1, 2,...,/EG/ с тем, что бы номер, присвоенный ребру, указывал, каким по счету это ребро проходится в эйлеровом цикле? Оказывается, это можно сделать, если нумеровать ребра, придержива­ясь следующих двух правил:

1. Начиная с произвольной вершины и, присваиваем произвольному ребру uv номер 1. Затем вычеркиваем ребро иv и переходим в вершину v.

2. Пусть w — вершина, в которую мы пришли в ре­зультате выполнения предыдущего шага, и k-- номер, присвоенный некоторому ребру на этом шаге. Выбираем любое ребро, инцидентное вершине w, причем мост вы­бираем только в том случае, когда нет других возмож­ностей; присваиваем выбранному ребру номер k +1 и вы­черкиваем его.

Этот процесс, называемый алгоритмом Флёри, закан­чивается, когда все ребра графа вычеркнуты, т. е. зану­мерованы.

Дадим теперь обоснование алгоритма. Прежде всего

заметим, что поскольку степень каждой вершины графа

G четна, то алгоритм может закончить работу только в той вершине, с которой начал. Поэтому он строит не­который цикл G, и надо только доказать, что этот цикл включает все ребра графа G. Предположим, что это не так, и пусть G' — связная компонента графа G — EC, не являющаяся изолированной вершиной. Рассмотрим мно­жество А ребер цикла С, инцидентных вершинам, вошед­шим в G'. Ясно, что А=0. Пусть а -ребро из А, полу­чившее в процессе работы алгоритма наибольший номер, т. е. вычеркнутое последним среди ребер А. Тогда, как легко видеть, ребро а к моменту вычеркивания было мос­том в графе. Однако это противоречит правилу выбора очередного ребра.

Заметим, что эйлеровы графы достаточно редки. Вер­на следующая

Теорема 43.4 (Р. Рейд, 1962 г.). Почти нет эйле­ровых графов.

Пусть ^i (/г) —множество всех эйлеровых графов из &(п) (см. § 12), а ^2 (и) — множество всех графов из &(п), степени всех вершин которых четны. Согласно тео­реме 43.1 имеем

(1)

Очевидно, что все графы из F2(п) можно получить, до­бавляя к некоторому графу из F(п— 1) новую вершину и соединяя ее со всеми вершинами нечетной степени.

Большая масса доказанных здесь теорем утверждает, что при выполнении определенных условий граф содержит гамильтонов цикл, причем метод доказательства таких теорем обычно дает и эффективный алгоритм построения са-мого гамильтонова цикла. В этом параграфе мы рассмот-рим несколько теорем такого рода (достаточных условий

гамильтоновости).

Интуитивно ясно, что если граф содержит много ребер и эти ребра к тому же достаточно равномерно распре делены, то граф «предрасположен» быть гамильтоновым. В трех приводимых ниже теоремах можно усмотреть

подтверждение этому.

Напомним, что степенной последовательностью графа называется список степеней его вершин.

Теорема 44.2 (В. Хватал, 1972 г.). Граф со степенной последовательностью d₁ ≤ d₂ ≤....≤d_n является гамилътоновым, если для всякого к, удовлетворяющего не равенствам 1≤к<п/2, истинна импликация

Теорему докажем от противного. Пусть существует негамильтонов граф, последовательность степеней вершин которого удовлетворяет условиям теоремы. Соединив две несмежные вершины такого графа ребром, получим, как легко видеть, граф со степенной последовательностью, снова удовлетворяющей условиям теоремы. Так как пол ный граф гамильтонов, то отсюда следует, что существу ет максимальный негамильтонов граф, степенная после довательность которого обладает таким же свойством. Этот граф будем обозначать через G. Таким образом, до бавление любого нового ребра к графу G приводит к по явлению в нем гамильтонова цикла. Поэтому любые две его несмежные вершины соединены гамильтоновой цепью. Выберем в графе G пару несмежных вершин v₁ и v_n так, чтобы величина deg v₁ + deg v_n была максимальной. Пусть v₁ ,v₂, ..., v_n — гамильтонова цепь, соединяющая

эти вершины.

Если в графе G вершины v₁ и v_j смежны, то вершина v_n не может быть смежной с v_j-1, поскольку в противном случае граф G содержал бы гамильтонов цикл

(v₁ ,v₂, ...,v_j-1 ,v_n , v_n-1 ,v_n-2 , ..., v_j+1 ,v_j+1 ,v₁)

(рис. 44.4). Таким образом, вершина v_n не смежна по крайней мере с deg v₁ вершинами, и поэтому deg v_n ≤ п — 1 — deg v₁. Отсюда получаем

deg v₁ + deg v_n ≤ n — 1< п.

Д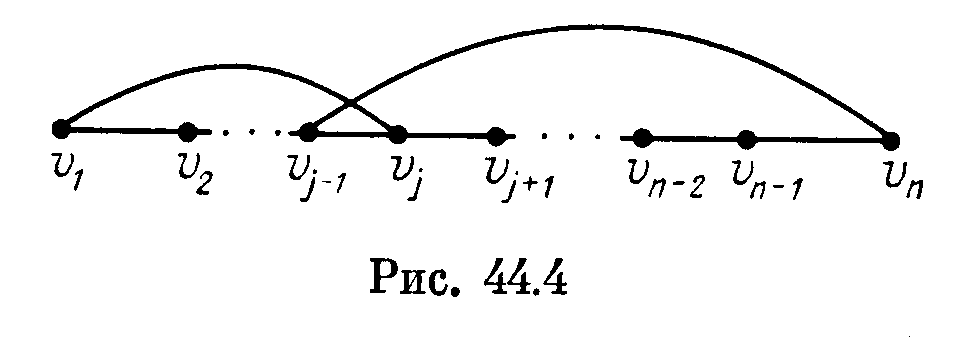 ля определенности будем предполагать, что deg v₁ ^ < deg v_n. Это вместе с предыдущим неравенством дает deg v₁ < п/2. Поскольку величина deg v₁ + deg v_n макси­мальна,то степень каждой вершины, не смежной с v_n, не превосходит deg v₁. При этом таких вершин, как уже

от­мечалось, не менее чем deg v₁. Поэтому выбрав k = deg v₁ , получим d_h≤ k< п/2. Следовательно, по условию теоремы d_n-_h ≥ п — k. Последнее означает, что имеется по крайней мере k + 1 вершин степени не меньше чем п — k. Такими вершинами являются, например, вершины со степенями d_n ,d_n-1 ,...., d_n-_k .Поскольку deg v₁ = k, то v₁ не может быть смежной со всеми этими вершинами, и, значит, найдется такая вершина v₁ не смежная с v₁, что deg v₁ ≥ ≥ п — k. Но тогда

deg v₁ + deg v_1t ≥ k + (n — k)> deg v₁ + deg v_n,

что противоречит выбору вершин v₁ и v_n.С помощью только что доказанной теоремы можно получить ряд других достаточных условий гамильтоновости. Эти условия проще и, естественно, слабее теоремы 44.2.

Теорема 44.3 (О. Оре, 1960 г.). Если для любой пары и и v несмежных вершин графа G порядка п≥3 выполняется неравенство deg и + deg v ≥ n, то G — га милътонов граф. > Пусть

VG = {v₁ , v₂ , ..., v_n }, di = deg v_i , i =1, n,

и d₁ ≤ d₂ ≤ . ..≤ d_n — степенная последовательность гра фа G. Согласно теореме 44.2 достаточно показать, что ус ловие нашей теоремы обеспечивает выполнение нера венств

d_h>k, k =.l,[n/2-1].

Доказательство проведем от противного. Пусть для не которого t € {1, ..., [n/2— 1]} выполняется неравенство

d_t < t. Существование индексов i и j таких, что i, j<t и v_iv_j¢EG, привело бы к неравенствам

d_i + d_i<2d_t <2t<n,

противоречащим условию теоремы. Следовательно, вер шины v₁ ,v₂ , ..., v_t попарно смежны. Это вместе с неравенствами d_i < t (l=1, t) означает, что каждая вершина v_i {1=1, t) смежна не более чем с одной вершиной v_m, t + 1 < т < п. Далее, поскольку t < п/2, то п — t > t. По этому найдется вершина v_i, t + 1 < j< п, не смежная ни с одной из вершин v_i ( i = l, t). Следовательно, deg v_i< < n - t - 1. Но тогда для пары несмежных вершин v_t и v_j имеем неравенство deg v_t + deg v_j < n , которое противоречит условию теоремы.

Из этой теоремы непосредственно вытекает следующая Теорема 44.4 (Г. Дирак, 1952 г.). Если |G|=n>3 и для любой вершины v графа G выполняется неравен­ство deg v > n/2, то G — гамильтонов граф.

Нетрудно заметить, что во всяком n-вершинном графе, удовлетворяющем условиям любой из рассмотренных выше теорем 44.2—44.4, число ребер не меньше чем (п—1)²/4. С другой стороны, n-вершинный планарный граф, как мы знаем, содержит не более Зn — 6 ребер. По­этому рассмотренные выше достаточные условия заведомо неприменимы к планарным графам.

Л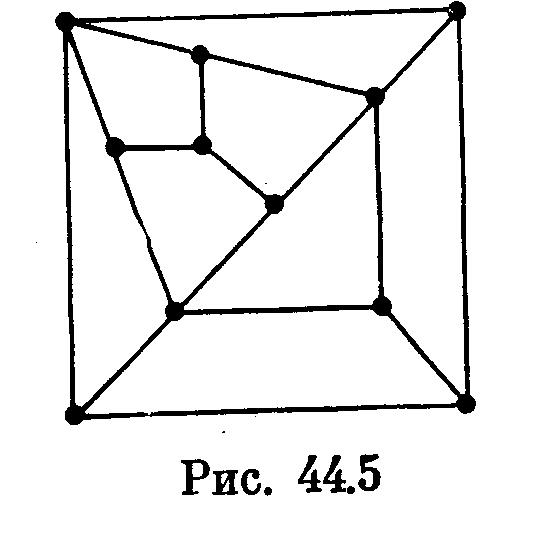егко указать 2-связный негамильтонов планарный граф. Таким графом является, например, тэтаграф. При­вести пример 3-связного планарного графа без гамильтонова цикла уже не столь просто. Такой граф, оказы­вается, должен содержать не менее 11 вершин. Этот факт был установлен Д. Барнеттом и Е. Юковичем (1970 г.). Найденный ими негамильтонов планарный 3-связный граф с минимальным числом вершин изо­бражен на рис. 44.5. В том, что этот граф не содержит гамильтонова цикла, можно убедиться, проделав не слишком большой в данном случае перебор вариантов. Проще, однако, заметить, что он — двудольный и, следовательно, не содержит циклов нечетной длины, в частности, гамильтоновых циклов.

Следующая теорема — один из наиболее сильных ре­зультатов, касающихся гамильтоновых графов.

Теорема 44.5 (У. Татт, 1946 г.). Всякий 4-связный планарный граф является гамилътоновым.

Весьма сложное доказательство этой теоремы здесь опускается.

Следствие 44.6 (X. Уитни, 1932 г.). Если в мак­симальном плоском графе G каждый 3-цикл является границей некоторой грани, то G — гамилътонов граф.

Как известно (следствие 39.2), всякий максималь­ный плоский граф 3-связен. Если же такой граф не яв­ляется 4-связным, то он необходимо содер­жит 3-цикл, не являю­щийся границей ника­кой грани (см. упр. 12 гл. VI).

П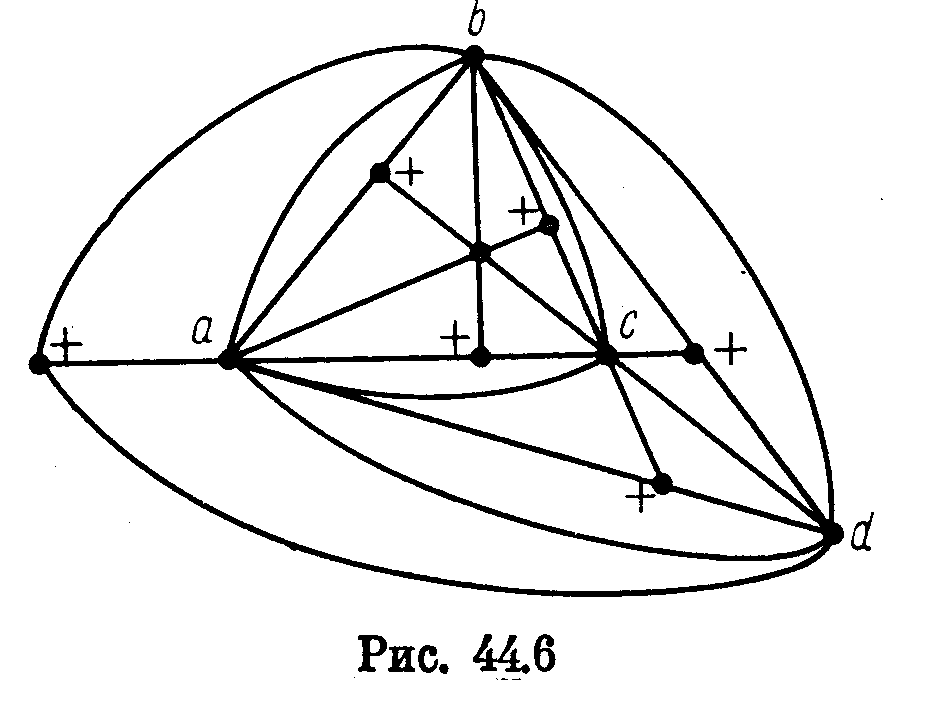ример максималь­ного планарного нега-мильтонова графа G с 11 вершинами приве­ден на рис. 44.6. От­сутствие гамильтонова

цикла следует из того, что шесть вершин графа G, по­меченных знаком «+», попарно не смежны, а на цикле длины 11 могут лежать не более пяти таких вершин. Согласно следствию 44.6, этот граф должен содержать 3-цикл, не являющийся границей никакой грани. Та­кими 3-циклами являются, например, (а, b, c) и (а, с, d).

Если в n-вершинном графе G фиксировать одну вер­шину и обход всегда начинать с нее, то всякому гамильтонову циклу очевидным образом будет соответствовать перестановка элементов множества VG. Тем самым най­ти гамильтонов цикл либо убедиться в отсутствии та­кого цикла можно путем перебора (n - 1)! перестановок. Если граф G гамильтонов, то проделать этот перебор в полном объеме придется только в случае крайнего неве­зения — когда нужная, т. е. отвечающая гамильтонову циклу перестановка встретится последней в этом процес­се. Если же G — негамильтонов граф, то действуя по­добным образом, придется в любом случае проверить все (n-1)! перестановок.

На практике не пользуются столь бесхитростным спо­собом распознавания гамильтоновости, а применяют раз­личные алгоритмы частичного перебора. Однако и там наблюдается такой же эффект — т. е. негамильтоновость становить, как правило, труднее, чем гамильтоновость. В этой ситуации были бы полезны необходимые условия гамильтоновости. Такие условия нужны и для построе-ния примеров негамильтоновых графов с заданными свой-ствами. К сожалению, для графов общего вида необходи-мые условия гамильтоновости неизвестны, за исключе-нием уже упоминавшегося банального факта, что гамиль-тонов граф должен быть 2-связным. Иначе обстоит дело с планарными графами.

Всякую грань плоского графа, граница которой со-держит ровно k ребер, назовем k-гранью.

Т еорема 44.7 (Э. Я. Гринберг, 1968 г.). Пусть Д — число k-граней плоского графа G. Если G — гамилъто-нов граф, то для каждого к > 3 существуют такие целые неотрицателъные числа f_k , f_k что

Пусть граф G содержит гамильтонов цикл С. Этот цикл делит плоскость на две части — ограниченную — D₁ и неограниченную — D₂. Тем самым граф G представ-ляется в виде объединения двух графов G₁ и G₂, со дер-жащихся в D₁ и D₂ соответственно. Ясно, что D₁

— грань графа G₂, D₂ — грань графа G₁ и EG₁ EG₂ = EC. Пусть — число k-граней графа G₁ отличных от D₂, a fa — число k-граней графа G₂, отличных от D₁. Очевидно, что

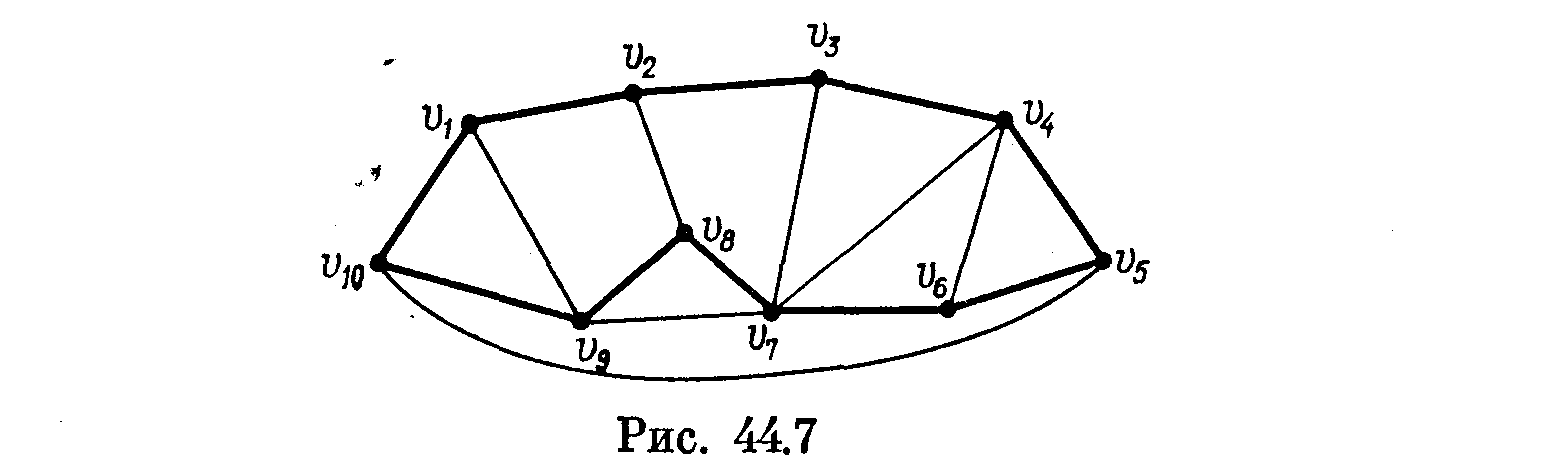
В графе G, изображенном на рис. 44.7, ребра гамиль-тонова цикла С обведены жирными линиями. Граф G₁ включает, помимо цикла С, ребра v₁v₉, v₂v₈, v₃v₇, v₄v₇, v₁v₆, а граф G₂ — ребра v₇v₉ и v₅v₁₀. В этом примере

f₃=5, f₄=2, f₅=f₆=1, f'₃=4, f'₄=2, f''₃=f''₅=f''₆=1,

остальные f_k,f'_k,f''_k равны 0.

Возвращаясь к доказательству, установим теперь справедливость равенства (1). С этой целью заметим, что удвоенное число ребер графа G₁ равно, а число всех его граней — . Поэтому, согласно формуле Эйлера, можем написать

П осле очевидных упрощений имеем

А налогичное соотношение верно и для графа G₂, т. е.

Объединив два последних равенства, получим (1).

Установление негамильтоновости графа путем пере­бора всех разбиений чисел f_k и последующей проверки выполнения равенства (1) едва ли проще полного пере­бора перестановок, о котором упоминалось выше. Польза теоремы 44.7 в другом — иногда удается, проанализиро­вав числа f_k, сразу сделать вывод об отсутствии подхо­дящего разбиения, т. е. вывод о негамильтоновости гра­фа. Рассмотрим в качестве примера граф, изображенный

на рис. 44.8. Для этого графа f₄=1, f₅=18, f₈=4, а ос­тальные f_k равны 0. Поэтому соотношение (1) должно иметь вид

2f'₄ +3f'₅ + 6f'₈=2f''₄ +3f''₄+6f''₈,

откуда следует, что f'₄=f''₄(mod 3). Это, однако, невоз­можно, поскольку f'₄+f''₄ =f₄=1 Таким образом, нужного разбиения чисел f_k не существует, и значит, граф негамильтонов.

Рассмотрим еще один класс теорем о гамильтоновых графах. В этих теоремах утверждается, что если граф G удовлетворяет определенным условиям, то граф, полу-чемый из G с помощью некоторой операции, гамиль-тонов.

Теорема 44.8 (Ф. Харари, С. Нэш-Вильямс, 1965 г.). Реберный граф L(G) гамилътонов тогда и только тогда, когда в графе G имеется цикл, содержащий хотя бы по одной вершине из каждого его ребра.

Из этой теоремы, приводимой здесь без доказатель­ства, вытекает, в частности, что если граф G является эйлеровым или гамильтоновым, то реберный граф L(G) гамильтонов.

Интуитивно ясно, что если граф G порядка п>3 связен, то при достаточно большом k граф G^k гамильтонов (определение графа G^k см. в § 8). Кроме того, в гамильтоновости графа G^k очевидно следует гамильтоновость графа G^k+l. В связи с этим представляет интерес наименьшее k, при котором граф G^k гамильтонов.

Теорема 44.9 (Д. Караганис, 1968 г.). Если графпорядка п>3 связен, то G³ — гамилътонов граф.

Теорему достаточно доказать для случая, когда - дерево. Будем доказывать следующее, несколько более сильное утверждение: для любого фиксированного ребра аb дерева G граф G³ содержит гамилътонов цикл, походящий через ab. Это утверждение легко проверить непосредственно для деревьев с числом вершин не более четырех. Предположим, что существуют деревья с большим числом вершин, для которых оно не верно. Выберем из них дерево Go с минимальным числом вершин, пусть аb — некоторое ребро дерева Go. При удалении любого ребра Go распадается на два дерева G1 и G2 таких, что aVG, bVG2. По крайней мере одно из них, например G1, содержит не менее трех вершин. Выберем вершину v VG1 так, чтобы ребро va принадлежало EG1.

поскольку \VG1\ <\VGo\, то G1 содержит гамильтонов цикл Н1, проходящий через ребро va.

Теперь рассмотрим дерево G2 Сначала допустим, что \VG2\>З, и пусть bx— ребро графа G2, инцидентное вершине b. Поскольку \VG₂\ < \VGo\, то G'3 содержит гамильтонов цикл H₂, проходящий через ребро bх. Ис-пользуя циклы H₁ и H₂, легко построить цикл H в графе G0, проходящий через ab. Для этого достаточно удалить ребра аv и bх из H₁ и H₂ соответственно и добавить реб­ра ab и xv, т. е. положить