Глава X Ориентированные графы

В приложениях часто приходится рассматривать гра­фы с ориентированными ребрами, т. е. ребрами, для ко­торых указаны начало и конец. Примерами таких графов являются сети автомобильных дорог с односторонним дви­жением или схемы программ для ЭВМ. Недостаточно простых (неориентированных) графов и для описания несимметричных отношений. Примерами подобных отно­шений могут служить порядок выполнения комплекса ра­бот, задаваемый с помощью сетевого графика, или тур­нирная ситуация в спортивных соревнованиях.

В этой главе изучаются ориентированные графы.

§ 63. Основные определения

Пусть V — конечное непустое множество, V² — его де­картов квадрат. Ориентированный граф (орграф)—это па­ра (V, А), где A V ². Элементы множества V называют­ся вершинами орграфа G — (V, А), а элементы множества А — его дугами. Таким образом, дуга — это упорядочен­ная пара вершин. Множества вершин и дуг орграфа G обозначаются через VG и AG соответственно. Число |VG| называется порядком орграфа G и обозначается через |G|.

Если х — (и, v) — дуга, то вершины и и v называются ее концевыми вершинами, причем и называется началом дуги x, a v — концом. Говорят, что дуга инцидентна каж­дой из своих концевых вершин. Говорят также, что дуга исходит из своего начала и заходит в свой конец. Дуга с совпадающими началом и концом, т.е. дуга вида (v, v), называется петлей. Можно определить ориентированные графы с несколькими дугами, имеющими общее начало и общий конец (мультиграфы). Такие дуги называются параллельными.

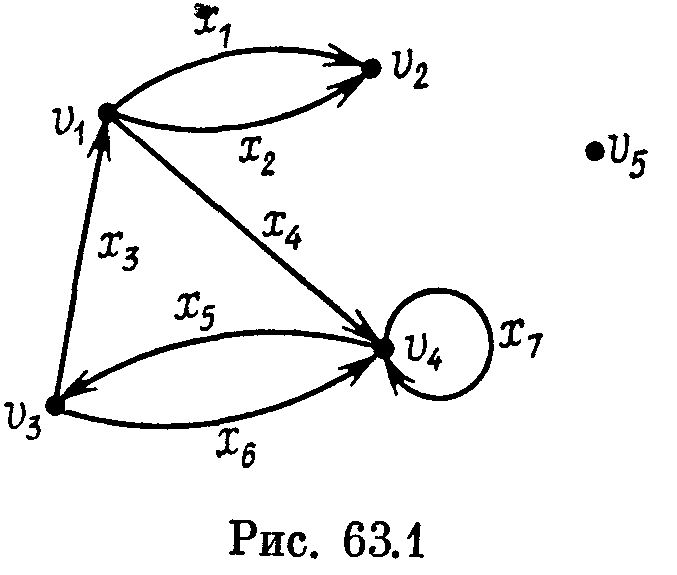
На рисунке дуга изображается направленной линией, идущей от начала дуги к концу. Направление линии обозначается стрелкой. Например, для графа G, представленного на рис. 63.1, VG = (v₁ , v₂ , v₃ , v₄ , v₅ ), AG ={x₁, x₂ , x₃, x₄, x₅, x₆ , x₇ }, причем x₁ и x₂ — параллель­ные дуги, а x₇ — петля.

Вершины орграфа называются смежными, если они являются концевыми для некоторой дуги. Дуги называ­ются смежными, если они имеют общую концевую вер­шину.

Пусть G — некоторый орграф. Ориентированным маршрутом (или просто маршрутом) в графе G называется:

такая последовательность S = (v₀, х₀ ,v₁, х₂, ..., х_п, v_n) (1) его чередующихся вершин v_i и дуг x_j что Xi = {Vi-1, Vi) (i= 1, п). Такой маршрут назо­вем (v₀, v_n)-маршрутом. Вер­шины v₀ и v_n назовем крайни­ми, а остальные вершины маршрута (1) — промежуточны­ми (внутренними). Длиной маршрута называется число входящих в него дуг. Маршрут называется цепью, если все входящие в него дуги различны, и путем, если все входящие в него вершины, кроме, возможно, крайних, различны.

Если в орграфе G нет параллельных дуг, то маршрут (1) может быть задан последовательностью входящих в него вершин: S = (v₀, v₁, ..., v_n). В любом случае маршрут можно задать последовательностью входящих в него дуг: S = (x₁, x₂, ..., х_п).

Маршрут называется циклическим, если его первая и последняя вершины совпадают. Циклический путь называется контуром. Очевидно, что любой (и, v)-маршрут при и ≠ v содержит (и, v)-путь, а при и = v — контур.

Последовательность (1) чередующихся вершин и дуг графа G, таких, что Xi = (v_i-1, v_i) или Xi = (v_i, v_i-1), называется полумаршрутом. Аналогично определяются полуцепъ, полупутъ и полуконтур.

Если в орграфе существует (и, v)-маршрут, то говорят, что вершина v достижима из вершины и. Любая вершина считается достижимой из себя самой.

Орграф называется сильным (или силъносвязным), ели любые две его вершины достижимы друг из друга. Орграф называется односторонним (или односторонне-связным), если для любой пары его вершин по меньшей мере одна достижима из другой. Орграф называется сла­бым (слабосвязным, связным), если любые две его вер­шины соединены полупутем.

Поскольку любая вершина графа достижима из себя, то одновершинный граф одновременно и сильный, и одно­сторонний, и слабый.

Очевидно, что каждый сильный граф является одно­сторонним, а каждый односторонний — слабым.

Очевидно также, что любые две несовпадающие вершины сильного орграфа принадлежат некоторому циклическому маршруту.

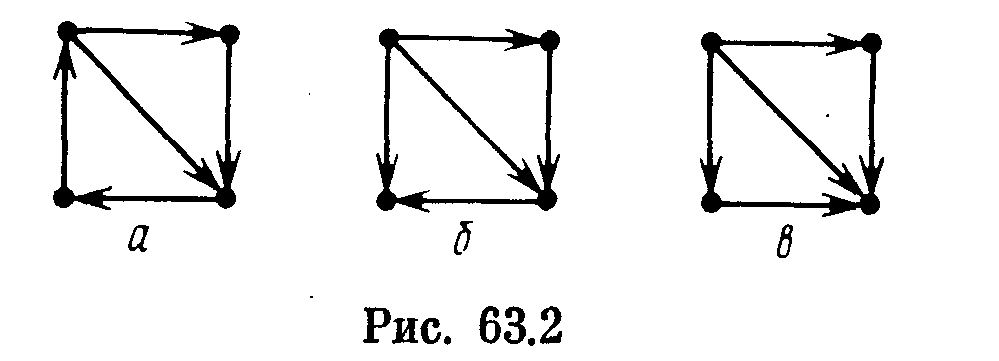
На рис. 63.2, а изображен сильный орграф, на рис. 63.2, б — односторонний, а на рис. 63.2, в — слабый.

Маршрут, содержащий все вершины орграфа G, на­зывается остовным.

Утверждение 63.1. Орграф является сильным тогда и только тогда, когда в нем есть остовный цикличе­ский маршрут.

> Необходимость. Пусть G — сильный орграф и Т = (v₀, х₀ ,v₁, х₂, ..., х_п, v₀)—его циклический маршрут, проходящий через максимально возможное число вершин. Если этот маршрут не является остовным, то возьмем вне его вершину и. Так как G — сильный орграф, то сущест­вуют маршруты

T₁ = (v₀, y₁, ..., v) T₂ = (v, z₁, ..., v₀).

Но тогда циклический маршрут

T'= (v₀, x₁, v₁ ..., x_n , v₀, y₁, ..., v, z₁, ..., v₀ )

содержит большее, чем Т, число вершин, что противоре­чит выбору маршрута Т. Следовательно, Т — остовный маршрут.

Достаточность. Пусть и и v — две произвольные вершины орграфа G, а

T = (v₀, х, ..., v, у, ..., и, z, ..., vo) — циклический маршрут. Тогда и достижима из v с по­мощью маршрута (v, у, ..., и) — части маршрута Т,— а v из и — с помощью маршрута (и, z, ..., vo, x, ..., v). <

Аналогично доказывается

Утверждение 63.2. Орграф является односторонним тогда и только тогда, когда в нем есть остовный маршрут. Орграф является слабым тогда и только тогда, когда в нем есть остовный полумаршрут.

Подграфы и порожденные подграфы ориентированного графа определяются так же, как и для неориентиро­ванного. Так же определяются и операции над орграфами.

Введем важное понятие сильной компоненты орграфа. Сильной (или сильносвязной) компонентой ориентированного графа называется любой его максимальный относительно включения сильный подграф.

Очевидно, что отношение взаимной достижимости вер­шин ориентированного графа G рефлексивно, симметрично и транзитивно. Следовательно, мы получим разбиение множества VG на классы, объединив в один класс все вершины, достижимые друг из друга. Подграфы, порожденные классами этого разбиения, и только они, служат сильными компонентами орграфа G.

В орграфе могут быть дуги, не входящие ни в одну из его сильных компонент.

Орграф G, изображенный на рис. 63.3, имеет четыре сильные компоненты с множествами вершин (v₁, v₂, v₃, v₄), (v₅, v₆, v₈), (v₇) и (v₉).

Пусть (S₁, S₂, ..., S_m) — множество всех сильных компонент ориентированного графа G. Конденсацией орграфа называется орграф G*, вершины s₁, s₂, ..., s_m которого соответствуют сильным компонентам орграфа G, и пара (s_i, s_j) является дугой в G* тогда и только тогда, когда в нем есть дуга, начало которой принадлежит компоненте S_i, конец — Sj.

На рис. 63.3 представлены орграф G и его конденсация G*.

Утверждение 63.3. Конденсация G* любого оргра­фа G не имеет контуров.

> Проведем доказательство от противного. Пусть Т = (so, xi, si, ..., so)— контур в G*. Тогда каждая вер­шина, входящая в компоненту S_i, достижима из любой вершины, входящей в компоненту S_j. Но это противоре­чит максимальности сильных компонент. <

Неориентированный мультиграф, получающийся в ре­зультате снятия ориентации с дуг орграфа G, называется основанием орграфа G и обозначается через G_b.

Очевидно, что орграф является слабым тогда и только тогда, когда его основание — связный мультиграф.

Орграф называется несвязным, если его основание — несвязный мультиграф.

Ориентированный граф называется турниром, если его основание является полным графом. Этот класс графов получил свое название в связи со спортивными турнира­ми без ничьих, проводимыми по круговой системе. Резуль­таты встреч можно описать ориентированным графом, вершины которого соответствуют участникам соревнова­ний, а дуга (и, v) есть в орграфе, если участник и побе­дил участника v.