§ 66. Пути

Пусть

(1)

— какое-либо множество путей орграфа G, попарно не имеющих общих вершин. Если множества VPi вершин этих путей составляют разбиение для VG, т. е.

то множество путей М называется разбиением орграфа G на пути. Минимальное число l путей, составляющих раз­биение орграфа G, обозначим через l(G).

Ниже фигурируют понятия числа независимости a₀{G) и хроматического числа χ(G) орграфа G, которые для ориентированных графов определяются так же, как и для неориентированных, т. е. a₀ (G)= a₀ (G₆), χ(G)= χ(G_b).

Теорема 66.1 (Т. Галлаи и А. Милгрэм, 1960 г.). Для любого орграфа G верно неравенство l(G) ≤ a₀ (G).

Фиксируем некоторое разбиение (1) орграфа G на пу­ти. Пусть N(M) = { a₁, a₂, ..., a_l), a_i Pi,— множество на­чальных вершин этих путей. Докажем более сильное ут­верждение:

существует такое разбиение М' орграфа G на пути, что

> Доказательство последнего утверждения проведем индукцией по n = |G|. Утверждение очевидно при п = 1, 2. Пусть п > 2 и утверждение верно для орграфов, порядки которых меньше п.

Вначале покажем, что, не ограничивая общности, мож­но считать |М| < a₀(G)+ 1. В самом деле, пусть |М| ≥ a₀(G)+ 2. Рассмотрим орграф G₁ = G — VP₁. Очевид­но, что a₀(G₁) ≤ a₀(G). Пo индуктивному предположе­нию существует разбиение М₁ орграфа G₁ на пути с

Пусть теперь |М| — a₀(G)+ 1. Тогда множество N(M) = (a₁, a₂, ..., a_l) не является независимым, т. е. в нем есть хотя бы одна пара смежных вершин. Предполо­жим, что (a₁, a₂) AG. Если путь P₁ состоит из единст­венной вершины a₁, то объединив P₁ и Р₂ в путь (a₁, a₂ ...), получим нужное разбиение.

Если же путь P₁=( a₁, b₁, ...) имеет более чем одну вершину, то рассмотрим орграф G₁ = G — a₁. По индук­тивному предположению существует такое разбиение М₁ орграфа G₁ на пути, что |М| < a₀(G₁) < a₀(G) и N(M₁)<={b₁, a₂, a₃, ..., a_l). Если b₁N(M₁), то М' полу­чим из M₁, добавив вершину а₁ к пути, начинающемуся в b₁. Аналогично можно поступить и тогда, когда а₂ N(M₁).

Из теоремы 66.1 вытекают два важных следствия.

Орграф G называется транзитивным, если истинна импликация

Следствие 66.2 (теорема Дилворта, 1950 г.). Если орграф G транзитивен, то l(G) = a₀(G).

> Согласно предыдущей теореме l(G) <= a₀(G). Но две вершины транзитивного орграфа, принадлежащие од­ной цепи, смежны, поэтому a₀(G)<= l(G). Итак, l(G) = a₀(G).

Следствие 66.3. В каждом турнире существует гамилътонов путь.

> Поскольку любые две вершины произвольного тур­нира Т смежны, то a₀(T)= 1. Поэтому существует цепь Р, содержащая все вершины турнира Т. <

Для сильных турниров верно следующее более общее утверждение.

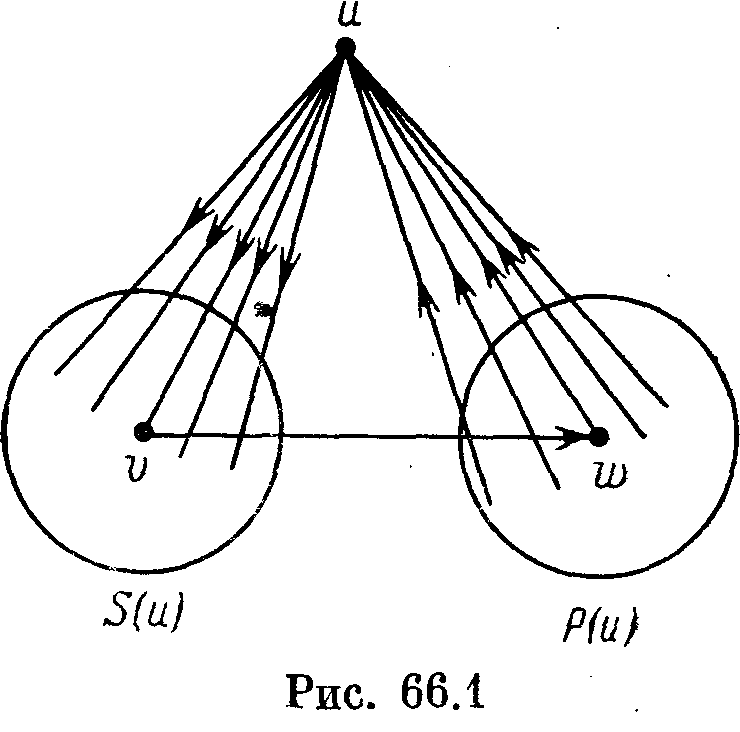
Теорема 66.4. Пусть Т — сильный турнир порядка п. Тогда для любой его вершины и и для любого числа k, 3 <k< п, в Т есть контур длины к, содержащий вер­шину и.

> Пусть S(и) и Р(и)— множество всех тех вершин v и, соответственно, w турнира Г, для которых (и, v) AT и (w, u)^AT. Оба эти множества не являются пу­стыми, поскольку орграф Т сильный. По той же причине существует хотя бы одна дуга (v, w), идущая из S(и) в Р(и) (рис. 66.1). Следовательно, вершина и лежит на контуре длины 3.

Далее воспользуемся индукцией по к. Пусть вершина и входит в контуры всех длин от 3 до к, где к < п. По­кажем, что она входит в контур длины к + 1.

Пусть C = (v₀, vi, ..., v_h), v_Q = v_k = и,— контур дли­ны к. Предположим, что для некоторой вершины w, не

входящей в этот контур, су­ществуют такие дуги (w, х) и (у, w), что х VC и уVC. Тогда в С есть такие две смежные вершины v_i и v_i+1, что (v_i, w) и (w, v_i+1)— дуги турнира Т (рис. 66.2). Сле­довательно, вершина и вхо­дит в контур длины к + 1.

Если же указанной выше вершины w нет, то множе­ство вершин турнира Т, не входящих в контур С, можно разбить на две части S(C) и Р(С) так, чтобы для любых вершин aS{C), bP(C) и v С выполнялись усло­вия (v,a) AG и (b, v) AG. Так как орграф T сильный, то S(C) и Р(С) не пусты и существует дуга, идущая из некоторой вершины aS(C) в некоторую вершину b Р(С) (рис. 66.3).

Таким образом, вершина u входит в контур длины к+1

Очевидно

Следствие 66.5. Сильный турнир гамилътонов.

Заметим, что предыдущее следствие вытекает также из теоремы 66.3.

Теорема 66.6 (Т. Галлаи и Б. Руа, 1967 г.). Если к — максимальная длина путей в орграфе G, то χ(G)< к + 1.

> Обозначим через В такое минимальное относительно включения подмножество в AG, что орграф G₁ = G — В не имеет контуров. Для любой вершины v определим t( v) как число вершин пути в орграфе G₁ с началом в v, имею­щем максимальную длину. Приписав каждой вершине и цвет t(v), получим раскраску орграфа G не более чем к + 1 цветами. Остается доказать, что эта раскраска пра­вильная, т. е. что t(и)<>t(v) для любых двух смежных вершин и и v. Но если (и, v) AG₁, то t(u)>t(v). Если же (a, v) B, то G₁ +(u, v) имеет контур. Поэтому в G₁ существует (v, u)-путь и, следовательно, t(v)> t(u).

Итак, доказано, что χ(G)< к + 1. <