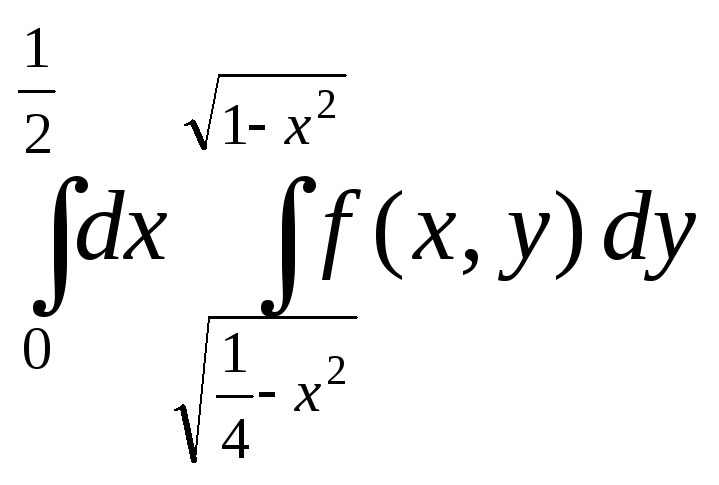4.3. Операционное исчисление

Определение 4.3. Изображением функции по Лапласу называется функция комплексного переменного, определяемая равенством

.

Если - изображение , то символически будем обозначать это так:

.

Пусть , , тогда справедливы следующие свойства преобразования Лапласа.

Свойства преобразования Лапласа.

1. Линейность: для любых комплексных постоянных и

.

2. Формула подобия: для любого

.

3. Дифференцирование оригинала: если функции ,,…,являются функциями-оригиналами, то

,

,

…………….

.

4. Дифференцирование изображения:

.

5. Интегрирование оригинала:

.

6. Интегрирование изображения: если является функцией-оригиналом, то

.

7. Формула смещения: для любого комплексного

.

8. Формула запаздывания:

.

9. Формула умножения изображений:

.

При отыскании оригинала по заданному изображению используют таблицы преобразования Лапласа и свойства, перечисленные выше. Выпишем фрагмент таблицы, достаточный для решения всех предложенных задач (таблица 4.1).

Таблица 4.1

Оригинал	Изображение

Пример 4.8. Найти оригинал по заданному изображению:.

Решение. Разложим дробь в сумму простейших дробей:

.

Опустим вычисления по нахождению неизвестных коэффициентов. В итоге получаем . Итак, разложение имеет вид:

.

Выделим полный квадрат в знаменателе:

.

Используя таблицу 4.1, находим:

,

,

,

Теперь преобразуем так, чтобы выделить явно эти выражения:

.

Тогда

.

Применение операционного исчисления к решению дифференциальных уравнений

С помощью преобразования Лапласа можно перейти от дифференциального уравнения в пространстве оригиналов к алгебраическому уравнению в пространстве изображений. Решив полученное алгебраическое уравнение, найдем с помощью обратного преобразования Лапласа оригинал, который и является решением исходного дифференциального уравнения.

Пример 4. 9. Решить задачу Коши: ,.

Решение. Пусть . Тогда ,

, .

Подставим все полученные выражения в исходное уравнение:

,

,

откуда ,.

Разложим дробь на сумму простейших дробей.

,

отсюда .

Если , то,.

При получаем,.

Если , то,.

Тогда

.

Пример 4. 10. Решить систему дифференциальных уравнений:

при ,.

Решение. Пусть ,, .

Получаем систему линейных уравнений относительно и:

, или .

Решим эту систему с помощью метода Крамера (метода определителей).

, .

Тогда ,.

Разложим на сумму простейших дробей:

, отсюда .

Если , то, .

При получаем,.

Тогда .

Разложим в сумму простейших дробей.

.

Отсюда .

Если , то, .

При получаем,.

Тогда .

Контрольная работа №7. «Кратные интегралы»

Задача 1. Изменить порядок интегрирования в двойном интеграле. Область интегрирования изобразить на чертеже.

1.1.	1.2.
1.3.	1.4.
1.5.	1.6.
1.7.	1.8.
1.9.	1.10.
1.11.	1.12.
1.13.	1.14.
1.15.	1.16.
1.17.	1.18.
1.19.	1.20.
1.21.	1.22.
1.23.	1.24.
1.25.	1.26.
1.27.	1.28.
1.29.	1.30.

Задача 2. Вычислить двойной интеграл.

2.1.	, .
2.2.	, .
2.3.	, .
2.4.	, .
2.5.	, .
2.6.	, .
2.7.	, .
2.8.	, .
2.9.	, .
2.10.	, .
2.11.	, .
2.12.	, .
2.13.	, .
2.14.	, .
2.15.	, .
2.16.	, .
2.17.	, .
2.18.	, .
2.19.	, .
2.20.	, .
2.21.	, .
2.22.	, .
2.23.	, .
2.24.	, .
2.25.	, .
2.26.	, .
2.27.	, .
2.28.	, .
2.29.	, .
2.30.	, .

Задача 3. Найти площадь фигуры, ограниченной данными линиями.

3.1.	, ,.
3.2.	, ,.
3.3.	, ,.
3.4.	, ,.
3.5.	, ,.
3.6.	, ,
3.7.	, ,,.
3.8.	, ,.
3.9.	, ,.
3.10.	, ,.
3.11.	, ,.
3.12.	, ,.
3.13.	, ,.
3.14.	, ,.
3.15.	, ,.
3.16.	, ,.
3.17.	, ,.
3.18.	, ,.
3.19.	, ,.
3.20.	, ,
3.21.	, ,.
3.22.	, ,.
3.23.	, ,.
3.24.	, ,.
3.25.	, ,.
3.26.	, ,.
3.27.	, ,.
3.28.	, ,.
3.29.	, ,.
3.30.	, ,.

Задача 4. Вычислить объем тела, ограниченного поверхностями.

4.1.	.
4.2.	.
4.3.	.
4.4.	.
4.5.	.
4.6.	.
4.7.	.
4.8.	.
4.9.	.
4.10.	.
4.11.	.
4.12.	.
4.13.	.
4.14.	.
4.15.	.
4.16.	.
4.17.	.
4.18.	.
4.19.	.
4.20.	.
4.21.	.
4.22.	.
4.23.	.
4.24.	.
4.25.	.
4.26.	.
4.27.	.
4.28.	.
4.29.	.
4.30.	.