Знакопеременные ряды

Ряд вида

,

(3.4)

где , называетсязнакочередующимся рядом.

Теорема 3.5 (признак Лейбница). Если для знакочередующегося ряда (3.4) и, то ряд(3.4) сходится.

Пусть

(3.5)

знакопеременный ряд, то есть любой его член , может быть как положительным, так и отрицательным.

Рассмотрим ряд, составленный из абсолютных величин членов ряда (3.5):

,

(3.6)

Теорема 3.6 (достаточный признак сходимости знакопеременного ряда). Если ряд (3.6) сходится, то сходится и ряд (3.5).

Определение 3.1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Пример 3.6. Исследовать на сходимость ряд .

Решение. 1. Исследуем на абсолютную сходимость. Рассмотрим ряд, составленный из абсолютных величин: . Воспользуемся предельным признаком сравнения. Сравним данный ряд с гармоническим рядом:.

Так как гармонический ряд расходится, то расходится и исследуемый ряд. Таким образом, абсолютной сходимости нет.

2. Исследуем ряд на условную сходимость. Воспользуемся признаком Лейбница. Так как

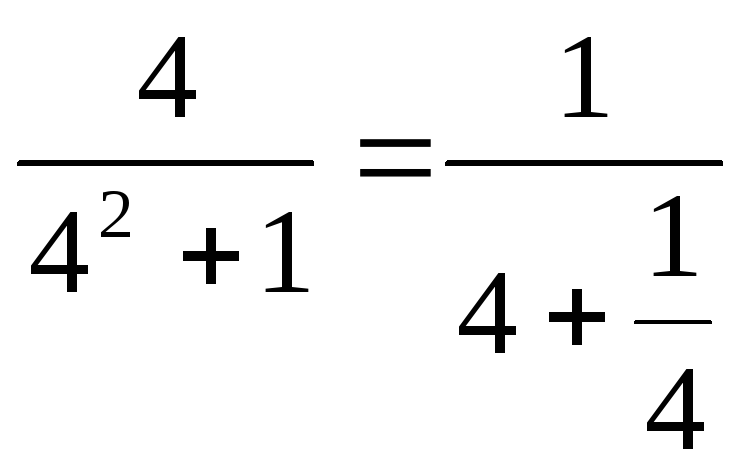, ,,, …., то

Следовательно, выполнено первое условие признака Лейбница. Далее, так как

,

то выполнено и второй условие. Значит, данный ряд сходится условно.

Степенные ряды

Функциональный ряд вида , где- действительные числа, называютстепенным.

Основное свойство степенных рядов состоит в том, что если степенной ряд сходится при , то он сходится, и притом абсолютно, при всяком значении, удовлетворяющем неравенству(теорема Абеля).

Одним из следствий теоремы Абеля является существование для всякого степенного ряда интервала сходимости , илис центром в точке, внутри которого ряд сходится абсолютно и вне которого расходится. На концах интервала сходимости (в точках) различные степенные ряды могут вести себя по-разному (сходиться абсолютно, условно или расходиться).

Число - половину длины интервала сходимости – называютрадиусом сходимости степенного ряда. В частных случаях радиус сходимости может быть равен нулю или бесконечности. Если, то степенной ряд сходится лишь при; если же, то ряд сходится на всей числовой прямой.

Для отыскания интервала и радиуса сходимости степенного ряда можно использовать следующие формулы:

,

.

Пример 3.7. Исследовать на сходимость степенной ряд .

Решение. Здесь ,. Имеем

.

Следовательно, ряд сходится, если , то есть.

Исследуем сходимость ряда на концах промежутка. Если , то получаем ряд, который сходится, так как является обобщенным гармоническим рядом с. Если, то получаем ряд. Этот ряд сходится (и притом абсолютно), так как сходится ряд из абсолютных величин его членов.

Итак, область сходимости (абсолютной сходимости) степенного ряда – отрезок .

Ряды Фурье

Пусть ,- две числовые последовательности. Тогда функциональный ряд вида

называется тригонометрическим рядом с периодом .

Теорема 3.7 (теорема единственности). Пусть функция интегрируема наи разлагается на этом отрезке в тригонометрический ряд, который допускает почленное интегрирование. Тогда коэффициенты этого разложения единственны и определяются формулами

, ,.

(3.7)

Определение 3.2. Тригонометрический ряд с периодом ,коэффициенты которого определяются формулами (3.7), называется рядом Фурье функции на отрезке.

Теорема 3.8 (о разложении функции в ряд Фурье). Пусть функция и ее производнаянепрерывны налибо имеют на нем лишь конечное число точек разрыва первого рода. Тогда ряд Фурье функциисходится на всей числовой оси. При этом сумма рядасовпадает св каждой точке непрерывности функциина, а на концах отрезка

.

Если же - точка разрыва функции, то

, где .

При этом - периодическая функция с периодом .

Условие Дирихле. Говорят, что функция удовлетворяет на отрезкеусловиям Дирихле, если существует конечное число точек, таких, что на каждом интервале,, она является ограниченной, непрерывной и монотонной.

Теорема 3.9 (Теорема Дирихле). Пусть функция удовлетворяет наусловиям Дирихле. Тогда ряд Фурье функциисходится на всей числовой оси. При этом сумма ряда Фурьесовпадает св каждой точке непрерывностина, а на концах отрезка

.

Если же - точка разрыва функции, то

, где .

При этом - периодическая функция с периодом .