4. Теория функций комплексного переменного. Операционное исчисление

4.1. Комплексные числа

Комплексным числом называется арифметическое выражение вида

,

(4.1)

где - действительные числа, а- специальный символ, который называетсямнимой единицей. Для мнимой единицы по определению считается, что .

(4.1) – алгебраическая форма комплексного числа, причем называетсядействительной частью комплексного числа, а -мнимой частью.

Число называетсякомплексно сопряженным к числу .

Пусть даны два комплексных числа ,.

1. Суммой комплексных чиселиназывается комплексное число

.

2. Разностью комплексных чиселиназывается комплексное число

.

3. Произведением комплексных чиселиназывается комплексное число

.

4. Частным от деления комплексного числана комплексное числоназывается комплексное число

.

Замечание 4.1. То есть операции над комплексными числами вводятся по обычным правилам арифметических операций над буквенными выражениями в алгебре.

Пример 4.1. Даны комплексные числа . Найти

.

Решение. 1) .

2) .

3)

.

4) Домножая числитель и знаменатель на комплексно сопряженное знаменателю число, получаем

.

Тригонометрическая форма комплексного числа:

,

где - модуль комплексного числа,- аргумент комплексного числа. Уголопределен неоднозначно, с точностью до слагаемого:

, .

- главное значение аргумента, определяемое условием

, (или ).

Показательная форма комплексного числа:

.

Корень й степени числа имеет различных значений, которые находятся по формуле

,

(4.2)

где .

Точки, соответствующие значениям , являются вершинами правильногоугольника, вписанного в окружность радиусас центром в начале координат.

Пример 4.2. Найти все значения корня .

Решение. Представим комплексное число в тригонометрической форме:

,

, откуда .

Тогда . Следовательно, по формуле (4.2)имеет четыре значения:

, .

Полагая , находим

, ,

, .

Здесь мы преобразовывали значения аргумента к его главному значению.

Множества на комплексной плоскости

Комплексное число изображается на плоскоститочкойс координатами. Модульи аргументсоответствуют полярным координатам точки.

Полезно помнить, что неравенство задает круг с центром в точкерадиуса. Неравенствозадает полуплоскость, расположенную правее прямой, а неравенство- полуплоскость, расположенную выше прямой. Кроме того, система неравенствзадает угол между лучамии, выходящими из начала координат.

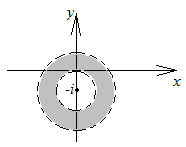
Пример 4.3. Нарисовать область, заданную неравенствами: .

Решение. Первому неравенству соответствует кольцо с центром в точке и двумя радиусами 1 и 2, окружности в область не входят (рис. 4.1).

Второму неравенству соответствует угол между лучами (биссектриса 4 координатного угла) и(положительное направление оси). Сами лучи в область не входят (рис. 4.2).

Искомая область является пересечением двух полученных областей (рис. 4.3)

рис. 4.1	рис. 4.2	рис. 4.3

4.2. Функции комплексного переменного

Пусть однозначная функция определена и непрерывна в области, а- кусочно-гладкая замкнутая или незамкнутая ориентированная кривая, лежащая в. Пусть, как обычно,,, где,- действительные функции переменныхи.

Вычисление интеграла от функции комплексного переменногосводится к вычислению обычных криволинейных интегралов, а именно

.

(4.3)

Если функция аналитична в односвязной области, содержащей точкии, то имеет место формула Ньютона-Лейбница:

,

(4.4)

где - какая-либо первообразная для функции, то естьв области.

В интегралах от функций комплексного переменного можно производить замену переменной, и интегрирование по частям аналогично тому, как это делается при вычислении интегралов от функций действительного переменного.

Заметим также, что если путь интегрирования является частью прямой, выходящей из точки , или частью окружности с центром в точке, то полезно делать замену переменной вида. В первом случае, а- действительная переменная интегрирования; во втором случае, а- действительная переменная интегрирования.

Пример 4.4. Вычислить по параболеот точкидо точки(рис 4.4).

рис. 4.4

Решение. Перепишем подынтегральную функцию в виде . Тогда ,. Применим формулу (4.3): . Так как , то,. Поэтому

.

Пример 4.5. Вычислить интеграл , где- дуга окружности,(рис. 4.5) .

рис. 4.5

Решение. Положим, , тогда,,. Получаем:

Функция , однозначная и аналитическая в кольце, разлагается в этом кольце вряд Лорана

.

(4.5)

В формуле (4.5) ряд называетсяглавной частью ряда Лорана, а ряд называетсяправильной частью ряда Лорана.

Определение 4.1. Точка называетсяизолированной особой точкой функции , если существует окрестность этой точки, в которой функцияаналитична всюду, кроме самой точки.

Функцию в окрестности точки можно разложить в ряд Лорана. При этом возможны три различных случая, когда ряд Лорана:

1) не содержит членов с отрицательными степенями разности , то есть

(ряд Лорана не содержит главной части). В этом случае называется устранимой особой точкой функции ;

2) содержит конечное число членов с отрицательными степенями разности , то есть

,

причем . В этом случае точка называется полюсом порядка функции ;

3) содержит бесконечное число членов с отрицательными степенями:

.

В этом случае точка называется существенно особой точкой функции .

При определении характера изолированной особой точки не обязательно искать разложение в ряд Лорана. Можно использовать различные свойства изолированных особых точек.

1) является устранимой особой точкой функции, если существует конечный предел функциив точке:

.

2) является полюсом функции, если

.

3) является существенно особой точкой функции, если прифункция не имеет предела, ни конечного, ни бесконечного.

Определение 4.2. Точка называетсянулем го порядка(или кратности ) функции , если выполняются условия:

…, .

Замечание 4.2. Точка тогда и только тогда является нулемго порядка функции , когда в некоторой окрестности этой точки имеет место равенство

,

где функция аналитична в точкеи

4) точка является полюсом порядка () функции, если эта точка является нулем порядкадля функции.

5) пусть -изолированная особая точка функции , где- функции аналитические в точке . И пусть точка является нулем порядка функциии нулем порядкафункции.

При точка является полюсом порядка функции.

При точка является устранимой особой точкой функции .

Пример 4.6. Найти изолированные точки и определить их тип для функции .

Решение. Функции и- аналитические во всей комплексной плоскости. Значит, особыми точками функцииявляются нули знаменателя, то есть точки, где. Таких точек бесконечно много. Во-первых, это точка, а также точки, удовлетворяющие уравнению. Отсюдаи.

Рассмотрим точку . В этой точке получим:

, ,

, .

Порядок нуля равен .

, ,

, ,

, ,

, .

Порядок нуля знаменателя равен .

Значит, точка является полюсом второго порядка ().

. Тогда

, .

Порядок нуля числителя равен .

, ,.

Порядок нуля знаменателя равен . Следовательно, точкиприявляются полюсами первого порядка (простыми полюсами).

Теорема 4.1. (Теорема Коши о вычетах). Если функция является аналитической на границеобластии всюду внутри области, за исключением конечного числа особых точек, то

.

При вычислении интегралов стоит аккуратно найти все особые точки функции , затем нарисовать контур и особые точки, и после этого выбрать только те точки, которые попали внутрь контура интегрирования. Сделать правильный выбор без рисунка часто бывает затруднительно.

Способ вычисления вычета зависит от типа особой точки. Поэтому, прежде чем вычислять вычет, нужно определить тип особой точки.

1) вычет функции в точке равен коэффициенту при минус первой степени в лорановском разложениив окрестности точки:

.

Это утверждение справедливо для всех типов изолированных точек, и поэтому в данном случае определять тип особой точки не обязательно.

2) вычет в устранимой особой точке равен нулю.

3) если - простой полюс (полюс первого порядка), а функциюможно представить в виде, где,(заметим, что в этом случае), тогда вычет в точкеравен

.

В частности, если , то.

4) если - простой полюс, то

.

(4.6)

5) если - полюсго порядка функции, то

.

(4.7)

Пример 4.7. Вычислить интеграл .

рис. 4.6

Решение. Находим особые точки подынтегральной функции . Функцияимеет две особые точкииВнутрь контура попадает только точка(рис. 4.6). Точка- полюс второго порядка, так какявляется нулем кратности 2 для функции.

Тогда по формуле (4.7) находим вычет в этой точке:

.

В силу теоремы 4.1 находим

.