Содержание

Предисловие……………………………………………………………………………………….. 3
1.	Интегральное исчисление функций одной переменной….………..……………………...	4
	1.1. Неопределенный интеграл……………………………………………………………...	4
	1.2. Определенный интеграл………………………………………………………………...	15
	1.3. Приложение определенного интеграла………………………………………………..	16
2.	Дифференциальное исчисление функций нескольких переменных……………………...	18
3.	Дифференциальные уравнения………………………………..…...……………………….	23
Контрольная работа №4…………………………………………………………………………...		34
Контрольная работа №5…………………………………………………………………………...		39
Контрольная работа №6…………………………………………………………………………...		45
Список литературы…...……………………………………………………………………………		47

Пояснительная записка

Цель преподавания математики в вузе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.

Настоящее пособие для студентов очно-заочной и ускоренной формы обучения всех технических специальностей содержит методические указания и контрольные задания по курсам интегрального исчисления, дифференциального исчисления функций нескольких переменных, дифференциальным уравнениям.

Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по учебной литературе, рекомендуемой в данном пособии.

Каждая задача контрольной работы содержит по 30 вариантов. Номер варианта расчетной работы определяется по последним двум цифрам номера зачетной книжки студента и соответствует этим цифрам, если они образуют число от 01 до 30. Если же число больше 30, то номер варианта равен остатку после деления этого числа на тридцать. Если же в остатке получен ноль, тогда ваш вариант 30.

1. Интегральное исчисление функций одной независимой переменной

1.1. Неопределенный интеграл

Рассмотрим основные методы отыскания неопределенного интеграла.

1. Непосредственное интегрирование. Данный метод основан на применении свойств неопределенного интеграла и таблицы основных интегралов.

Свойства неопределенного интеграла (правила интегрирования)

1. .

2. .

3. .

4. , где- постоянная.

5. .

6. Если и, то

Таблица основных интегралов

при

Пример 1.1. Найти интеграл .

Решение. Используя свойства 4 и 5, получаем

.

Пользуясь таблицей интегралов, получаем

.

Пример 1.2. Найти интеграл .

Решение.

.

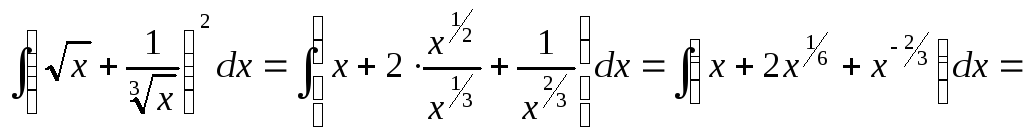
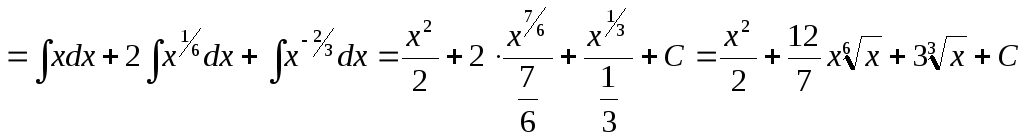Свойство 6 позволяет расширить таблицу основных интегралов с помощью приема внесения функции под знак дифференциала.

Пример 1.3. .

Решение. Этот интеграл можно привести к табличному интегралу, преобразовав его следующим образом:

Теперь переменной интегрирования служит выражение и относительно этой переменной получим интеграл от степенной функции. Следовательно,

.

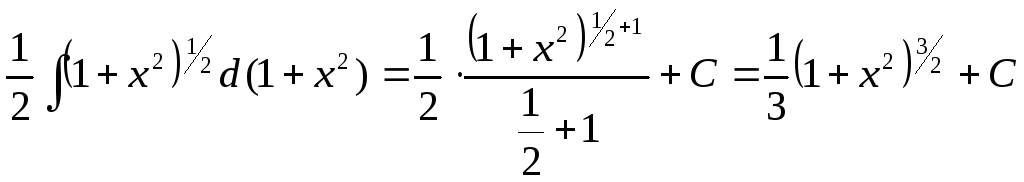Пример 1.4. .

Решение. Поступая так же, как и в примере 1.3, имеем:

.

Пример 1.5. .

Решение. Выражение можно записать как, поэтому

.

2. Замена переменной в неопределенном интеграле. Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:

1. , где- монотонная, непрерывно дифференцируемая функции новой переменной. Формула замены переменой в этом случае имеет вид

;

2. , где- новая переменная. Формула замены переменной при такой подстановке:

.

Пример 1.6. Вычислить интеграл: .

Решение. Воспользуемся подстановкой , то есть. Найдем дифференциал. Отсюда имеем

.

Ответ нужно выразить через старую переменную . Подставляя в результат интегрирования, получим

.

Пример 1.7. .

Решение. Положим , тогда, откуда. После подстановки в исходный интеграл получим

.

Замечание 1.1. Если интеграл является табличным, то интегралможно найти с помощью подстановки. Фактически саму подстановку можно не производить. Здесь достаточно принять во внимание, что. Таким образом,

,

где - первообразная для. Например,

, ,

и т.д.

Пример 1.8. .

Решение. Положим , тогда, откуда. После подстановки в исходный интеграл получаем

.

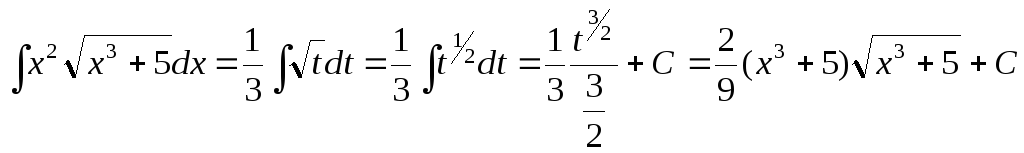Пример 1.9. , где.

Решение. Для того чтобы свести интеграл к табличному, разделим числитель и знаменатель подынтегрального выражения на :

.

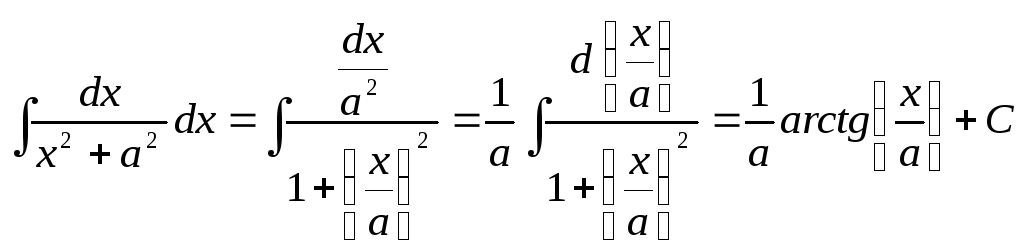Дополним теперь таблицу основных интегралов следующими формулами:

Пример 1.10. .

Решение. Выполним подстановку , тогда,и. Значит,

.

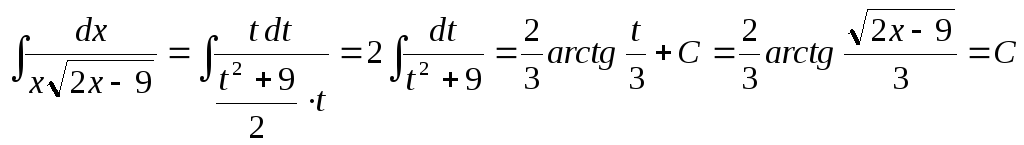Пример 1.11. .

Решение. Преобразуя знаменатель дроби, получим . Воспользуемся подстановкой, тогда. Отсюда

.

Пример 1.12. .

Решение. Положим , тогдаи

.

3. Интегрирование по частям. Интегрированием по частям называют нахождение интеграла по формуле

,

(1.1)

где ,- непрерывно дифференцируемые функции от.

Замечание 1.2. Для интегралов вида ,,, где- многочлен, в(1.1) за следует принять; для интегралов вида,,запринимают выражение.

Пример 1.13. .

Решение. Положим в (1.1) ,, тогда,. Используя формулу интегрирования по частям, получаем

.

Пример 1.14. .

Решение. Положим в (1.1) ,, тогда,. Используя формулу интегрирования по частям, получаем

.