1.3. Приложение определенного интеграла

Приведем некоторые приложения определенного интеграла.

Вычисление площади плоской фигуры

Площадь криволинейной трапеции, ограниченной кривой (где), прямыми,и отрезкомоси, вычисляется по формуле

.

Площадь фигуры, ограниченной кривыми и(где) прямымиивычисляется по формуле

.

(1.6)

Если кривая задана параметрическими уравнениями , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми,и отрезкомоси, вычисляется по формуле

,

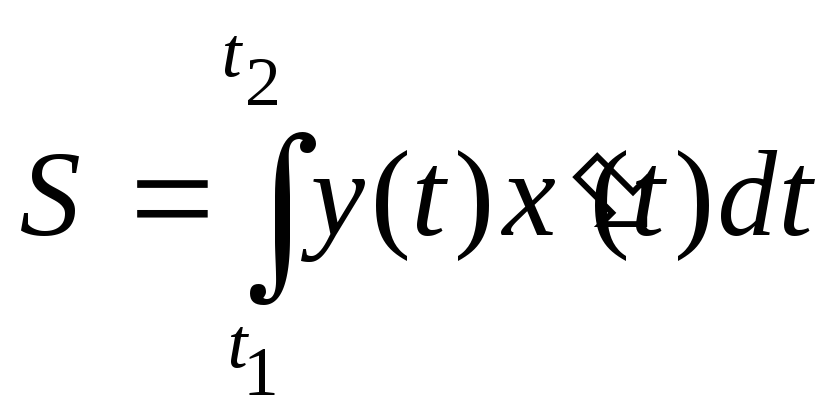где иопределяются из уравнений,, апри.

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами,(), находится по формуле

.

Пример 1.27. Вычислить площадь фигуры, ограниченной параболой и прямой(рис 1.1).

	Решение. Найдем точки пересечения прямой и параболы. Для этого решим уравнение , . Откуда ,. Тогда по формуле (1.6) имеем . .
рис. 1.1

Вычисление длины дуги плоской кривой

Если кривая на отрезке- гладкая (то есть производнаянепрерывна), то длина соответствующей дуги этой кривой находится по формуле

.

При параметрическом задании кривой (- непрерывно дифференцируемые функции) длина дуги кривой, соответствующая монотонному изменению параметраотдо, вычисляется по формуле

.

(1.7)

Если гладкая кривая задана в полярных координатах уравнением ,, то длина дуги выражается формулой

.

(1.8)

Пример 1.28. Вычислить длину дуги кривой ,,.

Решение. Найдем производные по параметру :,. Тогда по формуле (1.7) получаем

.

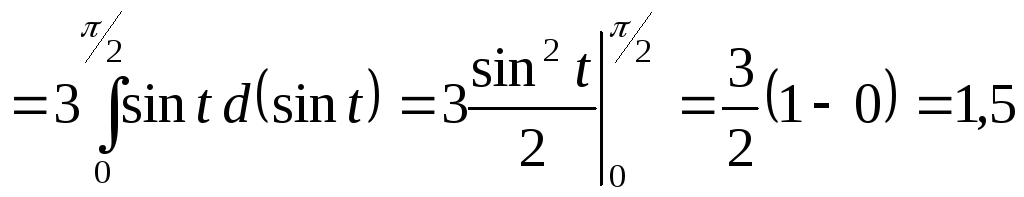2. Дифференциальное исчисление функций нескольких переменных

Пусть каждой упорядоченной паре чисел из некоторой областисоответствует определенной число. Тогданазываетсяфункцией двух переменных и,-независимыми переменными или аргументами, -областью определения функции, а множество всех значений функции -областью ее значений и обозначают .

Геометрически область определения функции обычно представляет собой некоторую часть плоскости , ограниченную линиями, которые могут принадлежать или не принадлежать этой области.

Пример 2.1. Найти область определения функции.

Решение. Данная функция определена в тех точках плоскости , в которых, или. Точки плоскости, для которых, образуют границу области. Уравнениезадает параболу (рис. 2.1; поскольку парабола не принадлежит области, то она изображена пунктирной линией). Далее, легко проверить непосредственно, что точки, для которых, расположены выше параболы. Областьявляется открытой и ее можно задать с помощью системы неравенств: .

рис. 2.1

Если переменной дать некоторое приращение, аоставить постоянной, то функцияполучит приращение, называемоечастным приращением функции по переменной:

Аналогично, если переменная получает приращение, а остается постоянной, то функция получит приращение, называемоечастным приращением функции по переменной :

.

Если существуют пределы:

,

,

они называются частными производными функции по переменными соответственно.

Замечание 2.1. Аналогично определяются частные производные функций любого числе независимых переменных.

Замечание 2.2. Так как частная производная по любой переменной является производной по этой переменной при условии, что остальные переменные – постоянны, то все правила дифференцирования функций одной переменной применимы для нахождения частных производных функций любого числа переменных.

Пример 2.2. Найти частные производные функции .

Решение. Находим:

,

.

Пример 2.3. Найти частные производные функции .

Решение. Находим:

,

,

.

Полным приращением функции называется разность

.

Главная часть полного приращения функции , линейно зависящая от приращений независимых переменных и,называется полным дифференциалом функции и обозначается . Если функция имеет непрерывные частные производные, то полный дифференциал существует и равен

,

где ,- произвольные приращения независимых переменных, называемые их дифференциалами.

Аналогично, для функции трех переменных полный дифференциал определяется выражением

.

Пусть функция имеет в точкечастные производные первого порядка по всем переменным. Тогда векторназываетсяградиентом функции в точкеи обозначаетсяили.

Замечание 2.3. Символ называется оператором Гамильтона и произносится “намбла”.

Пример 2.4. Найти градиент функции в точке.

Решение. Найдем частные производные:

, ,

и вычислим их значения в точке :

, ,.

Следовательно, .

Производной функции в точке по направлению вектора называют предел отношенияпри:

, где .

Если функция дифференцируема, то производная в данном направлении вычисляется по формуле:

,

где ,- углы, который векторобразует с осямиисоответственно.

В случае функции трех переменных производная по направлению определяется аналогично. Соответствующая формула имеет вид

,

(2.1)

где - направляющие косинусы вектора.

Пример 2.5. Найти производную функции в точкев направлении вектора, где.

Решение. Найдем вектор и его направляющие косинусы:

, ,,.

Вычислим значения частных производных в точке :

, ,;,,.

Подставляя в (2.1), получаем

.

Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка:

,

,

,

Частные производные ,называютсясмешанными. Значения смешанных производных равны в тех точках, в которых эти производные непрерывны.

Пример 2.6. Найти частные производные второго порядка функции .

Решение. Вычислим предварительно частные производные первого порядка:

, .

Продифференцировав их еще раз, получим:

, ,

, .

Сравнивая последние выражения, видим, что .

Пример 2.7. Доказать, что функция удовлетворяет уравнению Лапласа

.

Решение. Находим:

, .

, .

Тогда

.

Точка называетсяточкой локального максимума (минимума) функции , если для всех точек, отличных оти принадлежащих достаточно малой ее окрестности, выполняется неравенство

().

Максимум или минимум функции называется ее экстремумом. Точка, в которой достигается экстремум функции, называется точкой экстремума функции.

Теорема 2.1 (Необходимые условия экстремума). Если точка является точкой экстремум функции, тоили хотя бы одна из этих производных не существует.

Точки, для которых эти условия выполнены, называются стационарными или критическими. Точки экстремума всегда являются стационарными, но стационарная точка может и не быть точкой экстремума. Чтобы стационарная точка была точкой экстремума, должны выполняться достаточные условия экстремума.

Введем предварительно следующие обозначения:

, ,,.

Теорема 2.2 (Достаточные условия экстремума). Пусть функция дважды дифференцируема в окрестности точкии точкаявляется стационарной для функции. Тогда:

1. Если , то точкаявляется экстремумом функции, причембудет точкой максимума при() и точкой минимума при ().

2. Если , то в точкеэкстремума нет.

3. Если , то экстремум может быть, а может и не быть.

Пример 2.8. Исследовать на экстремум функцию .

Решение. Так как в данном случае частные производные первого порядка всегда существуют, то для нахождения стационарных (критических) точек решим систему:

, ,

откуда ,,,. Таким образом, получили две стационарные точки:,.

Находим:

, ,.

Для точки получаем:, то есть в этой точке экстремума нет. Для точкиполучаем:и, следовательно

в этой точке данная функция достигает локального минимума: .