Одномерное рассеяние

Рассеяние – это изменение состояния частицы при взаимодействии с препятствием в виде потенциального барьера.

Частица с энергией 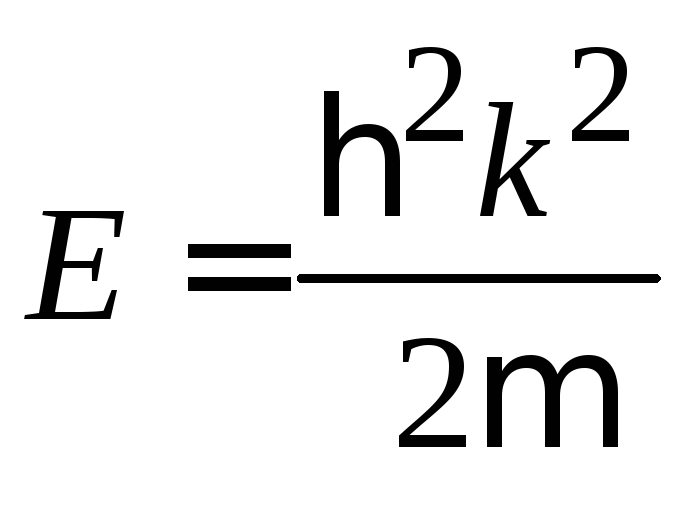движется вдоль оси x в состоянии плоской волны с единичной амплитудойи попадает в поле барьера с потенциальной энергией . В результате взаимодействия возникают отраженная и проходящая волны. При одномерном рассеянии отраженная волна движется против осиx, проходящая – вдоль оси x. Рассеянные волны отличаются амплитудами и фазами.

Рассеянные волны и их токи вероятности. Используем стационарное уравнение Шредингера (3.2) на больших расстояниях от барьера

,

где

– волновые числа при . Частные решения уравнения:

при падающая волна

(3.62)

и отраженная волна

; (3.63)

при проходящая волна

. (3.64)

Амплитуды отраженной и проходящей волн r и t – комплексные, поскольку рассеянные волны получают фазовые сдвиги.

Из (2.72)

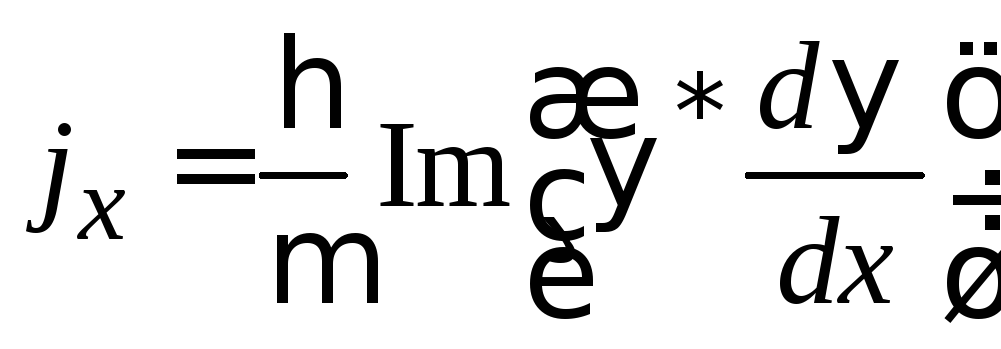
находим проекции плотности тока вероятности падающей, отраженной и проходящей волн

,

,

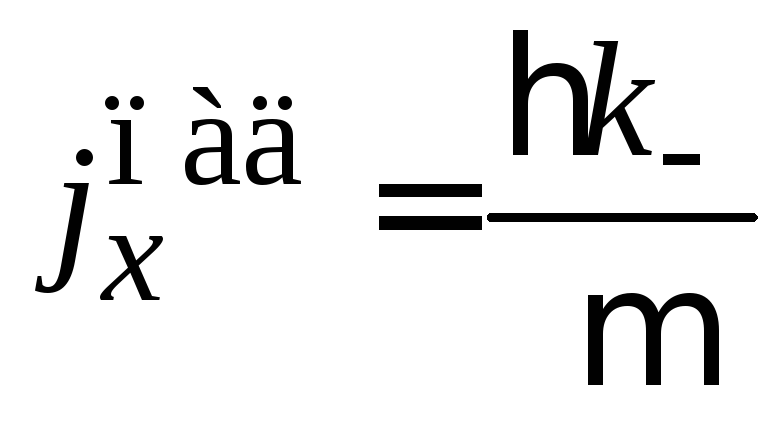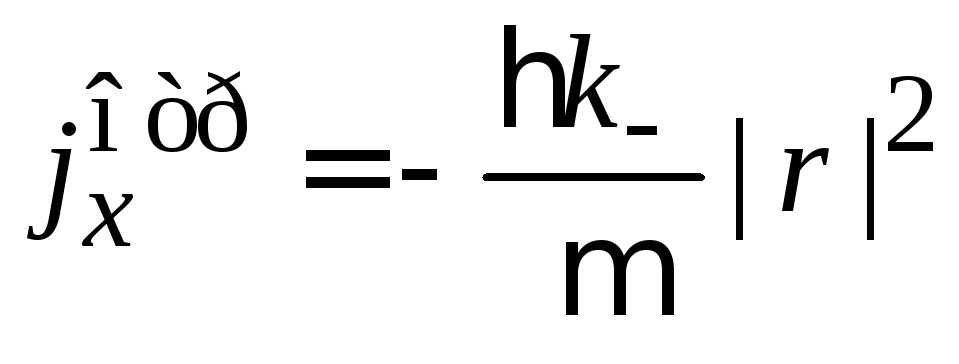. (3.65)

Токи регистрируются детекторами в физическом эксперименте.

Коэффициент отражения (reflection) определяем в виде

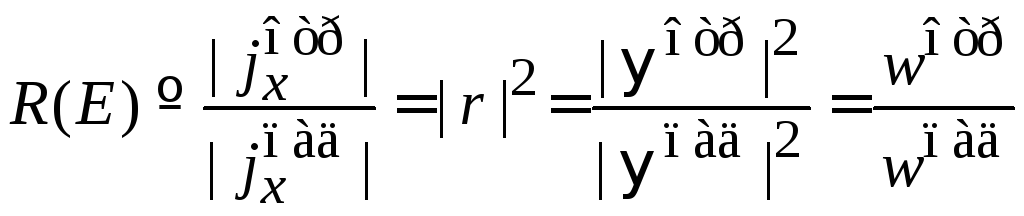, (3.66)

где учтены (3.65), (3.62) и (3.63)

, ,

,.

Тогда

. (3.67)

Коэффициент прохождения (transmission) определяем в виде

, (3.68)

тогда

, (3.69)

где .

Условие унитарности. Из уравнения непрерывности тока вероятности

, (2.73)

с учетом того, что на барьере частицы не рождаются и не накапливаются, получаем

,

тогда

.

Следовательно, сумма модулей подходящих к барьеру токов равна сумме модулей уходящих токов

– аналог первого правила Кирхгофа. Для проекций токов

. (3.70)

Используя (3.67) и (3.69)

, ,

получаем условие унитарности, от лат. unítas – «одно целое»:

(3.72)

– сумма вероятностей всех возможных процессов в системе, т. е. отражения и прохождения, равна единице.

Туннельный эффект

Если полная энергия частицы меньше потенциальной энергии барьера, то классическая частица не проходит через барьер, за барьером ее импульс становится мнимым, а кинетическая энергия – отрицательной. В квантовой механике частица имеет вероятность пройти барьер. Явление называется туннельным эффектом. Его описал Георгий Антонович Гамов в 1928 г. и объяснил парадокс, связанный с α-распадом ядра урана

.

Два протона и два нейтрона ядра урана объединяются в кластер и образуют α-частицу с энергией 4,18 МэВ. Задерживающий потенциал ядра урана составляет 8,57 МэВ. Тем не менее, α-частица имеет вероятность выхода из ядра благодаря туннельному эффекту и ядро распадается за время полураспада . Причина распада в том, что волновая функция не равна нулю в области не доступной для классической частицы. Термин туннельный эффект ввел Вальтер Шоттки в 1931 г.

Туннельный эффект лежит в основе множества явлений квантовой механики. На его основе разработан туннельный микроскоп и туннельный транзистор. Рассмотрим эффект, используя метод ВКБ.

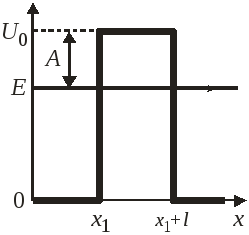
Движение частицы через барьер. Частица с энергией 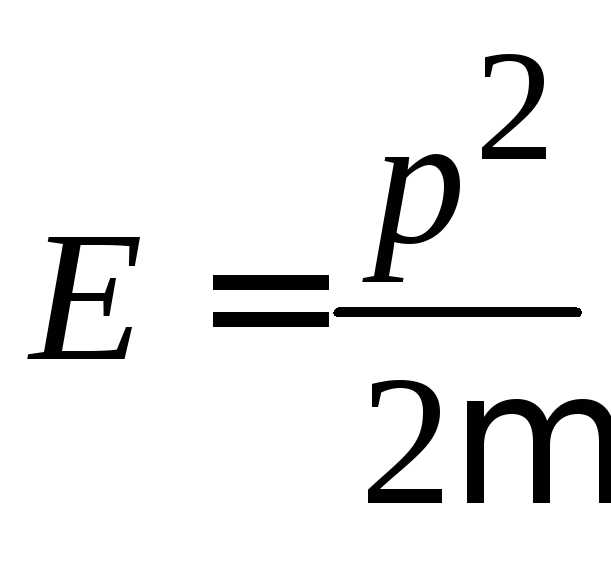в виде бегущей волны

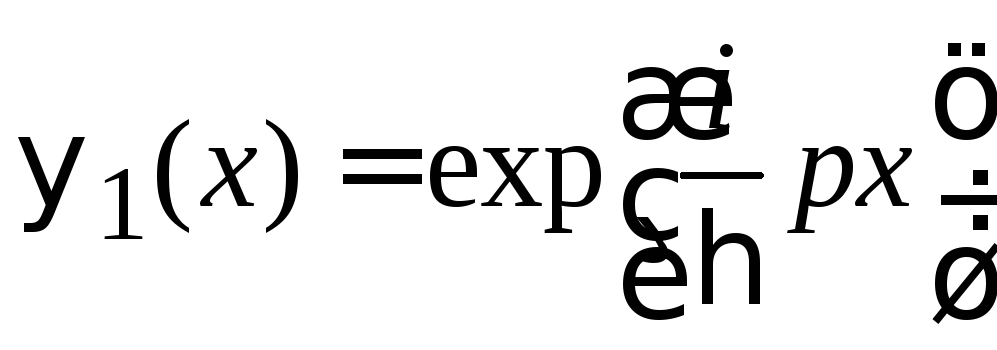
движется вдоль оси x и встречает барьер , превышающий ее полную энергию:

, ,

где и– точки остановки классической частицы.

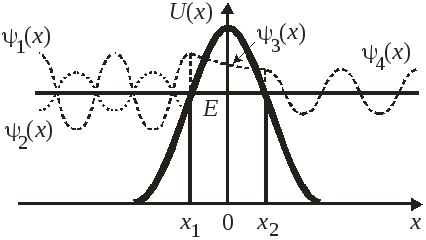
Возникает отраженная волна

.

Внутри барьера используем приближение ВКБ (3.60) в виде затухающей волны

.

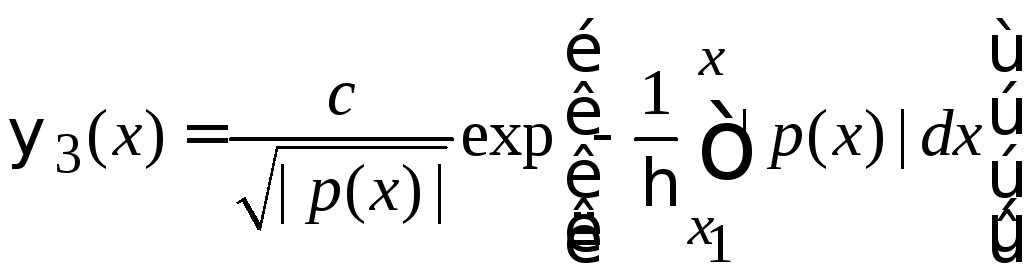За барьером возникает бегущая волна

.

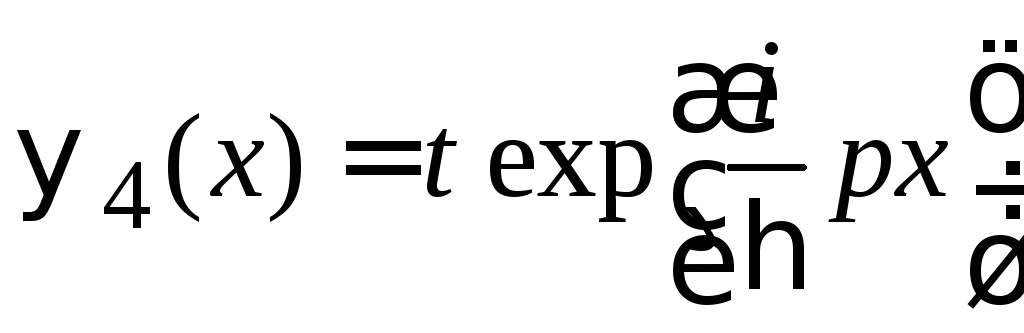Коэффициент прохождения барьера получаем из (3.68)

.

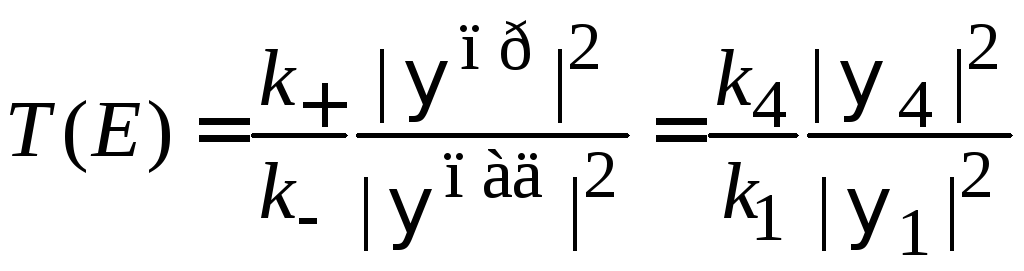При находим

,

где в случае малости отраженной волны учтены условия сшивания (3.11)

, .

Используем

,

,

из

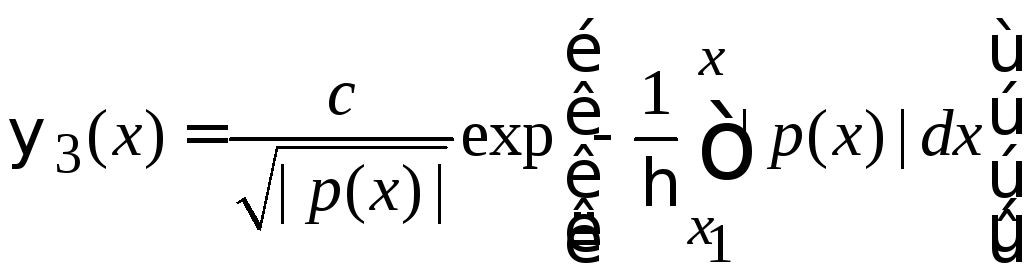
находим

,

.

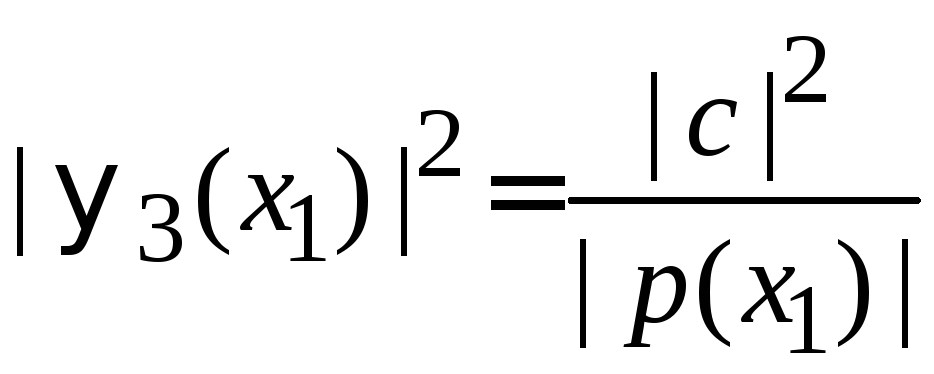С точностью до слабо меняющегося и близкого к единице предэкспоненциального множителя из 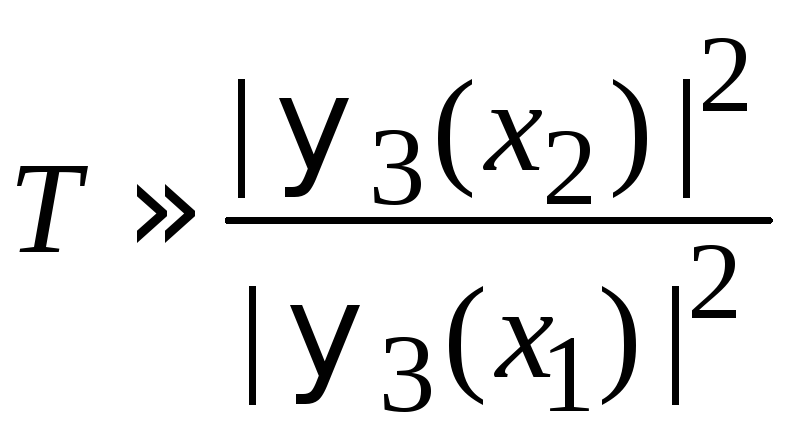получаем формулу Гамова

. (3.73)

Для прямоугольного барьера шириной и высотойиз (3.73) находим

, (3.73а)

где – работа выхода;– коэффициент затухания волны. Проницаемость барьера существенна при, тогда, и это ограничивает ширину барьера

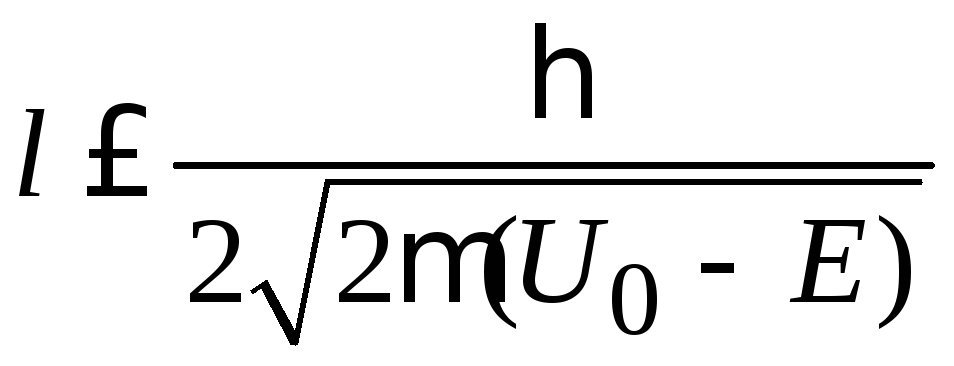. (3.74)

Чем меньше масса частицы, тем более широкий и высокий барьер она преодолевает. Массы электрона и протона отличаются в 1840 раз, тогда коэффициенты прохождения с одинаковой энергией через один и тот же барьер согласно (3.73а) различаются в раза. Для макроскопического тела туннельный эффект не проявляется.

Объяснение туннельного эффекта. Используем соотношение неопределенностей между импульсом и координатой

.

Если частица обнаруживается внутри барьера шириной l, то , и частица получает случайное возмущение импульса

.

Это изменяет ее кинетическую энергию на величину

.

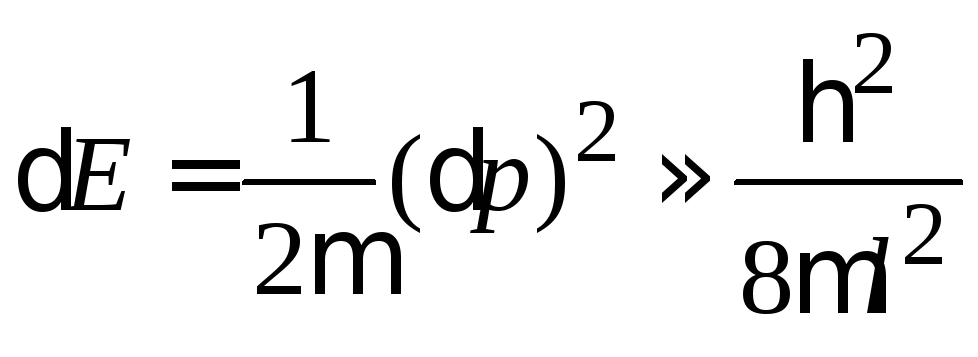Если энергия добавляется

,

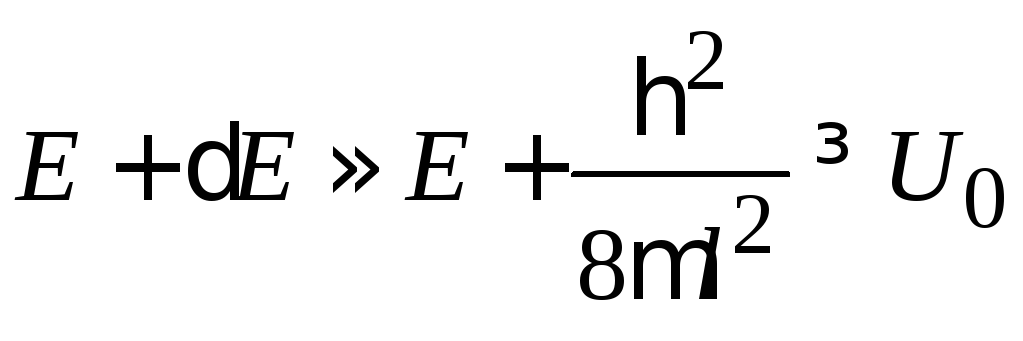то преодолевается барьер шириной (3.74).

Сканирующий туннельный микроскоп (СТМ) измеряет микрорельеф поверхности проводящего предмета с помощью туннельного эффекта. Работа СТМ основана на сильной зависимости туннельного тока от ширины барьера. Игла из платины, вольфрама или иридия с атомарным острием подводится к поверхности сначала двигателем грубого перемещения, затем пьезосканером на расстояние ≤ 1 нм, которое контролируется с высокой точностью по величине туннельного тока. На иглу подается потенциал (0,01–10) В по отношению к поверхности. Туннельный ток I через вакуумный промежуток размером l пропорционален коэффициенту прохождения (3.73а)

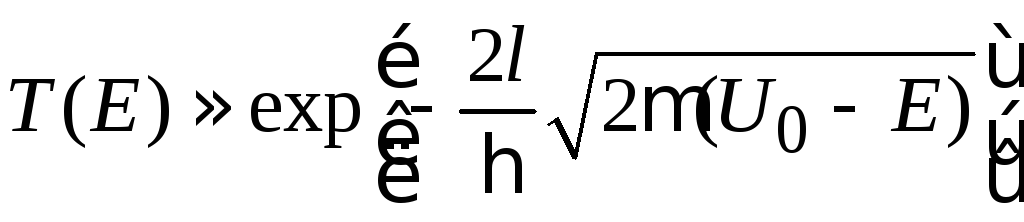
и экспоненциально зависит от l. При ток. Перемещение иглы наменяет ток в 10 раз. Игла периодически передвигается вдоль поверхности. Ток поддерживается на одном уровне за счет перемещения иглы перпендикулярно поверхности. Регистрируемые перемещения иглы дают рельеф поверхности. При использовании высокого вакуума и низких температур достигается разрешение по нормали к поверхности ~0,005 нм, в плоскости ~0,2 нм. Изменение расстояния на 0,1 нм изменяет туннельный ток на порядок. Возможно наблюдение отдельных атомов. Атом водорода в основном состоянии имеет размер ~0,1 нм. Фактически СТМ отображает рельеф плотности электронных состояний на поверхности объекта. Малая величина используемого потенциала не разрушает объект. СТМ может работать при нормальной температуре на воздухе, что снижает разрешение до ~1 нм, но требует изоляции от вибраций. СТМ разработали в 1981 г. Герд Биннинг (на фото слева) и Генрих Рорер (справа). На фото перед ними находится СТМ. Нобелевская премия 1986 г.

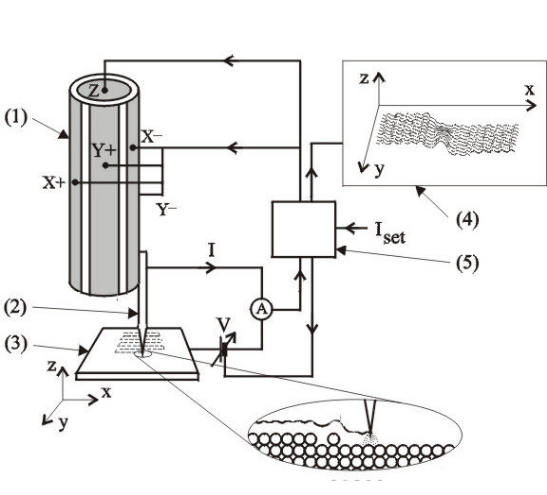
1– пьезо-сканер; 2 – игла; 3 – исследуемый образец;

4 – изображение на дисплее; 5 – электронное управление.

Поверхность Si(111)

(размытость изображения вызвана тепловыми флуктуациями)

Поверхность Cu(111)

Игла СТМ позволяет измерить потенциал точки поверхности проводника со сложной структурой и протекающим током.

При помощи СТМ измеряется распределение тока, протекающего между двумя контактами в плоскости двумерного проводника. Отрицательный потенциал иглы, касающейся проводника в точке , рассеивает упорядоченно движущиеся электроны, и проводимость проводникауменьшается тем сильнее, чем больше плотность тока в изучаемой точке. Распределение изменений проводимости, где– проводимость без касания иглы, дает распределение тока по проводнику. Метод предложенM.A. Topinca et al. Science 289, 2323 (2000).

СТМ измеряет также энергетическую плотность состояний поверхности проводника путем вариации приложенного к игле напряжения. Теория метода будет далее рассмотрена.

Повышение туннельного напряжения до ~10 В позволяет достичь в области острия с атомарными размерами электрического поля напряженностью до ~10⁸ В/см и плотности тока до ~10⁸ А/см². Такое поле может оторвать атом и перенести его на поверхность, или с поверхности. Это позволяет манипулировать атомами и молекулами с целью преобразования поверхности.