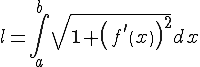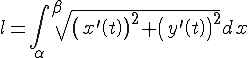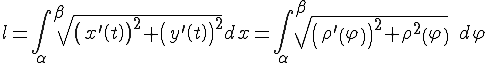Свойства
Невырожденность:
Положительность: Если интегрируемая функция f неотрицательна, то её интеграл по отрезку
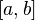 также
неотрицателен.
также
неотрицателен.Линейность: Если функции
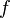 и
и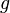 интегрируемы,
и
интегрируемы,
и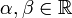 ,
то функция
,
то функция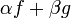 тоже
интегрируема, и
тоже
интегрируема, и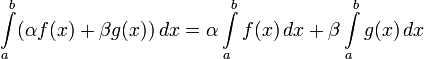 .
.Непрерывность: Если интегрируемые функции
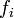 равномерно
сходятсяна отрезке
равномерно
сходятсяна отрезке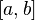 к
функции
к
функции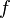 ,
то
,
то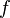 интегрируема,
и
интегрируема,
и
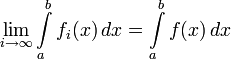 .
(Последняя формула может быть получена
уже как формальное следствие свойств
1-3 и интегрируемости предельной функции.)
.
(Последняя формула может быть получена
уже как формальное следствие свойств
1-3 и интегрируемости предельной функции.)Аддитивность при разбиениях отрезка Пусть
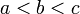 .
Функция
.
Функция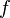 интегрируема
на отрезке
интегрируема
на отрезке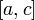 ,
тогда и только тогда, когда она
интегрируема на каждом из отрезков
,
тогда и только тогда, когда она
интегрируема на каждом из отрезков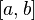 и
и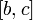 ,
при этом
,
при этом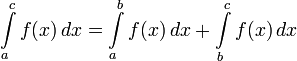 .
.Непрерывная на отрезке функция интегрируема по Риману (следствие свойств 1-5). Разрывные функции могут быть интегрируемы, но могут и не быть; примером функции, не интегрируемой по Риману, является всюду разрывная функция Дирихле.Критерий Лебега интегрируемости функции по Риману: функция интегрируема по Риману на отрезке
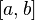 ,
если и только если на этом отрезке она
ограничена, и множество точек, где она
разрывна, имеет нулевую меру (то есть
может быть покрыто счётным семейством
интервалов со сколь угодно малой
суммарной длиной).
,
если и только если на этом отрезке она
ограничена, и множество точек, где она
разрывна, имеет нулевую меру (то есть
может быть покрыто счётным семейством
интервалов со сколь угодно малой
суммарной длиной).Если функция
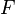 являетсяпервообразнойнепрерывной функции
являетсяпервообразнойнепрерывной функции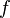 ,
то интеграл функции
,
то интеграл функции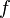 на
отрезке
на
отрезке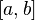 может
быть вычислен по формуле Ньютона-Лейбница:
он равен
может
быть вычислен по формуле Ньютона-Лейбница:
он равен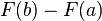 .
(Это - общее свойство любых интегралов,
удовлетворяющих свойствам 1-5, а не
только интеграла Римана.) Непрерывная
на отрезке функция
.
(Это - общее свойство любых интегралов,
удовлетворяющих свойствам 1-5, а не
только интеграла Римана.) Непрерывная
на отрезке функция всегда
имеет первообразную, и каждая первообразная
имеет вид:
всегда
имеет первообразную, и каждая первообразная
имеет вид: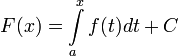 ,
где
,
где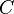 -
произвольная константа.
-
произвольная константа.
Формула Ньютона-Лейбница
|
Пусть
в определенном интеграле
Теорема
1.
Если
Замечание.
Из теоремы следует, что если функция
Теорема
2. Если
Эта формула называется формулой Ньютона-Лейбница.
Полагая,
|
|
41.Теорема.
Пусть
|
42. Интегрирование по частям в определенном интеграле
|
Пусть
Так
как
или окончательно
– формула интегрирования по частям в определенном интеграле. |
Несобственные интегралы
|
Определение.
Пусть функция
то
его называют несобственным
интегралом первого рода
от функции
Следовательно, по определению, имеем
Говорят
в этом случае, что несобственный
интеграл
то
его называют несобственным
интегралом второго рода
от функции
В
этом случае говорят, что интервал
сходится или существует. Если
и
либо
тогда
интегралы
|
Вычисление площадей с помощью определенных интегралов
|
1.
Пусть на отрезке
где
Итак, площадь криволинейной трапеции, ограниченной положительной функцией равна
Если
функция
Если
функция
Площадь
фигуры ограниченной графиками двух
непрерывных функций
Полученная
формула верна как для случая
|
Площади криволинейных трапеций и секторов
|
2.
Площадь криволинейной трапеции,
ограниченной сверху кривой, заданной
параметрически уравнениями
Если
3.
Площадь криволинейного сектора.
Вычислим
площадь сектора, ограниченного кривой,
заданной в полярных координатах
в
каждом углу зафиксируем произвольным
образом
Таким образом, получим веерообразную фигуру, площадь которой приближенно равна площади криволинейного сектора:
Полученная
сумма является интегральной суммой
для функции
Таким образом,
|
Вычисление длин дуг кривых с помощью определенных интегралов
|
1.
Пусть в прямоугольных координатах
на плоскости задана кривая уравнением
Обозначим
Пусть
По
теореме Лагранжа
и длина ломаной равна
Полученную
сумму можно считать интегральной
суммой функции
Итак, получили формулу для вычисления длины дуги:
2.
Найдем теперь длину дуги кривой
заданной параметрически уравнениями
или
3.
Пусть кривая задана в полярных
координатах уравнением
Найдем
производные от
Тогда
Следовательно,
|
47.
1. Пусть в прямоугольных координатах на
плоскости задана кривая уравнением
![]() .
Найдем длину дуги
.
Найдем длину дуги![]() этой
кривой, заключенной между вертикальными
прямыми
этой
кривой, заключенной между вертикальными
прямыми![]() и
и![]() .
Возьмем
на дуге
.
Возьмем
на дуге![]() точки
точки![]() с
абсциссами
с
абсциссами![]() и
проведем отрезки
и
проведем отрезки![]() ,
длины которых обозначим соответственно
через
,
длины которых обозначим соответственно
через![]() .
Тогда получим ломаную
.
Тогда получим ломаную![]() ,
вписанную в дугу
,
вписанную в дугу![]() .
Длина ломаной равна
.
Длина ломаной равна
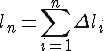 .
.
Обозначим
![]() –
параметр разбиения дуги
–
параметр разбиения дуги![]() .
Длиной
дуги называется предел, к которому
стремится длина вписанной ломаной, при
.
Длиной
дуги называется предел, к которому
стремится длина вписанной ломаной, при![]() :
:
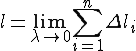 .
.
Пусть
![]() .
Найдем длину одного сегмента ломаной
.
Найдем длину одного сегмента ломаной![]() ,
координаты концов которой
,
координаты концов которой![]() ,
,![]() .
.
![]() .
.
По
теореме Лагранжа
![]() ,
такая, что
,
такая, что![]() .
Обозначим
.
Обозначим![]() ,
тогда
,
тогда
![]()
и длина ломаной равна
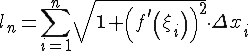 .
.
Полученную
сумму можно считать интегральной суммой
функции
![]() .
Так как функция
.
Так как функция![]() непрерывна,
то существует конечный предел
непрерывна,
то существует конечный предел![]() и
он равен определенному интегралу:
и
он равен определенному интегралу:
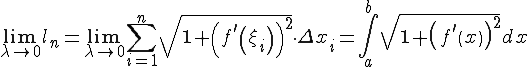 .
.
Итак, получили формулу для вычисления длины дуги:
|
|
(1) |
2.
Найдем теперь длину дуги кривой заданной
параметрически уравнениями
![]() ,
где функции
,
где функции![]() ,
причем
,
причем![]() .
Пусть
.
Пусть![]() .
В этом случае на отрезке
.
В этом случае на отрезке![]() определена
некоторая функция
определена
некоторая функция![]() ,
непрерывно дифференцируемая на этом
отрезке, и ее производная
,
непрерывно дифференцируемая на этом
отрезке, и ее производная![]() .
В интеграле (1) сделаем подстановку
.
В интеграле (1) сделаем подстановку![]() ,
получим
,
получим
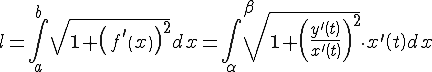
или
|
|
(2) |
3.
Пусть кривая задана в полярных координатах
уравнением
![]() ,
и
,
и![]() .
Для
нахождения длины дуги воспользуемся
формулой (2). Для этого представим
декартовы координаты через полярные
по формулам
.
Для
нахождения длины дуги воспользуемся
формулой (2). Для этого представим
декартовы координаты через полярные
по формулам![]() ,
в которые вместо
,
в которые вместо![]() подставим
подставим![]() :
:
![]() .
.
Найдем
производные от
![]() и
и![]() по
параметру
по
параметру![]() :
:
![]() .
.
Тогда
![]()
![]()
![]() .
.
Следовательно,
|
|
48.
Если вокруг оси
![]() вращается
криволинейная трапеция, ограниченная
непрерывной линией
вращается
криволинейная трапеция, ограниченная
непрерывной линией![]() ,
отрезком
,
отрезком![]() и
прямыми
и
прямыми![]() и
и![]() ,
то полученная от вращения фигура
называетсятелом
вращения.
,
то полученная от вращения фигура
называетсятелом
вращения.
Объем тела вращения вычисляется по формуле
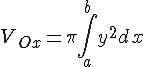 .
.
Если
зависимость
![]() задана
параметрически:
задана
параметрически:
![]() ,
,
то объем тела вращения равен
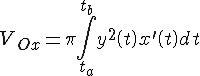 .
.
Если
криволинейная трапеция, ограничена
графиком непрерывной функции
![]() ,
прямыми
,
прямыми![]() ,
,![]() ,
то объем тела, образованного вращением
этой трапеции вокруг оси
,
то объем тела, образованного вращением
этой трапеции вокруг оси![]() ,
равен
,
равен
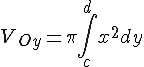 .
.
Если
зависимость
![]() задана
параметрически:
задана
параметрически:
![]() ,
,
то
объем тела вращения вокруг оси
![]() равен
равен
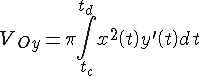 .
.
В более сложных случаях вращающуюся фигуру рассматривают как сумму или разность криволинейных трапеций и для каждой ситуации адаптируют «рабочую»
формулу.

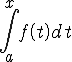 нижний
предел
нижний
предел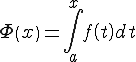 .
.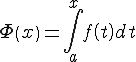 ,
то имеет место равенство:
,
то имеет место равенство: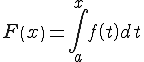 .
.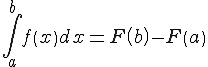 .
.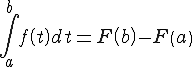 .
.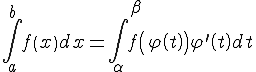 .
.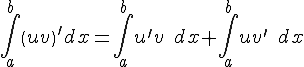 .
.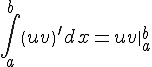 ,
поэтому равенство может быть записано
в виде:
,
поэтому равенство может быть записано
в виде: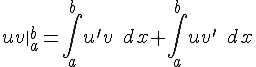
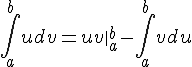
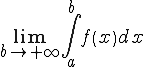 ,
,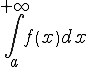 .
.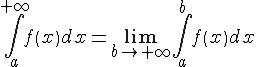 .
.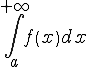 сходится
или существует. Если
сходится
или существует. Если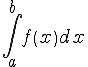 при
при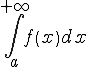 расходится,
или не существует.
Определение.
Пусть функция
расходится,
или не существует.
Определение.
Пусть функция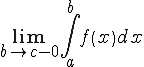 ,
,
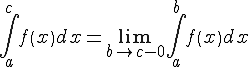 .
.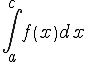 при
при следует
сходимость интеграла
следует
сходимость интеграла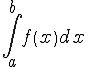 ,
а из расходимости
,
а из расходимости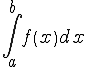 следует
расходимость
следует
расходимость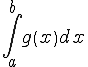 .
Теорема
(достаточный
признак сходимости, признак сравнения
в предельной форме). Пусть
.
Теорема
(достаточный
признак сходимости, признак сравнения
в предельной форме). Пусть
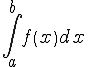 и
и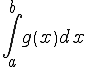 одновременно
сходятся или расходятся.
Теорема
(об
абсолютной сходимости). Если
интеграл
одновременно
сходятся или расходятся.
Теорема
(об
абсолютной сходимости). Если
интеграл
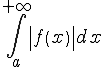 сходится,
то сходится и интеграл
сходится,
то сходится и интеграл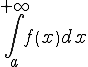 (в
этом случае его называют абсолютно
сходящимся).
(в
этом случае его называют абсолютно
сходящимся).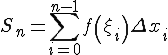 ,
,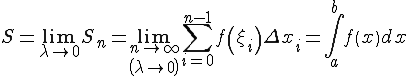 .
.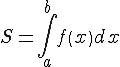
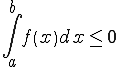 ,
а по абсолютной величине интеграл
равен площади криволинейной трапеции,
лежащей ниже оси
,
а по абсолютной величине интеграл
равен площади криволинейной трапеции,
лежащей ниже оси
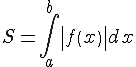
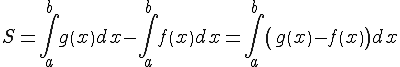
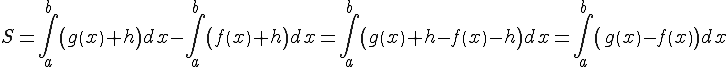
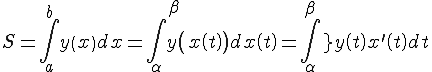
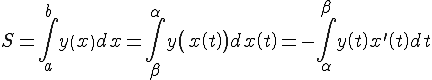 .
.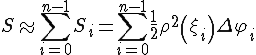 .
.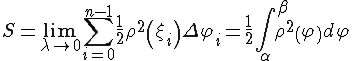 .
.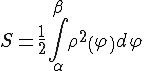 .
.
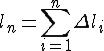 .
.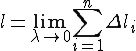 .
.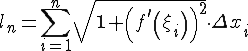 .
.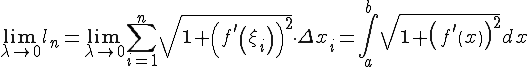 .
.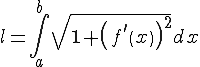

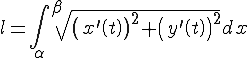
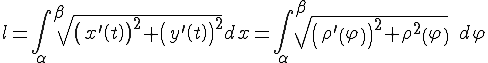
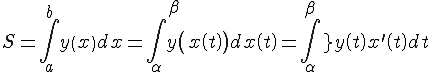
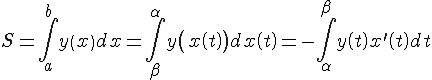 .
.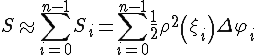 .
.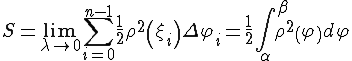 .
.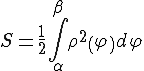 .
.