35. Замена переменной в неопределенном интеграле

     Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:      а) , где– монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:;      б), гдеU– новая переменная. Формула замены переменной при такой подстановке:.Интегрирование по частям

     Нахождение интеграла по формуленазывается интегрированием по частям. ЗдесьU=U(х),υ=υ( x) непрерывно дифференцируемые функции отх. С помощью этой формулы нахождение интеграла сводится к отысканию другого интеграла, ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.      При этом за υ берется такая функция, которая при дифференцировании упрощается, а заdU– та часть  подынтегрального выражения, интеграл от которой известен или может быть найден.      Так например, для интегралов вида,,, гдеP(x) – многочлен, за υ следует принятьP(x), а заdUсоответствует выражение,. Для интегралов видаза υ принимаются соответственно функции, а за– выражениеP(x)dx.

     36. Интегрирование рациональных дробей

     Рациональной дробью называется дробь вида , гдеP(x) иQ(x) – многочлены. Рациональная дробь называется правильной, если степень многочленаP(x) ниже степени многочленаQ(x); в противном случае дробь называется неправильной.      Пусть необходимо найти интеграл от неправильной рациональной дроби. При помощи деления (по правилу деления многочленов)  неправильную рациональную дробь можно представить в виде суммы целой рациональной функции и правильной рациональной дроби. Например,.      Затем знаменатель правильной дроби разлагается на множители вида, а правильная дробь разлагается на сумму элементарных дробей следующим образом: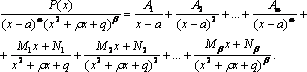37. Для интегрирования иррациональной функции, содержащейиспользуется подстановка. Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степенейx, применяется подстановка в форме, гдеnполагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию. Рациональная функцияxпод знаком корняn-ой степени, т.е. выражение вида, интегрируется с помощью подстановки.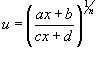

Универсальная тригонометрическая подстановка. Переход в подынтегральной функции к переменнойпреобразуетR(sinx, cosx) в функцию, рационально зависящую отt.Универсальная тригонометрическая подстановка всегда рационализирует подынтегральную функцию, с её помощью легко берутся интегралы вида(a,b,c- постоянные).

Универсальной тригонометрической подстановкойназываются выражение тригонометрических функций через тангенс половинного аргумента.

sinx=2tgx21+tg2x2x=+2nnZ;

cosx=1+tg2x21−tg2x2x=+2nnZ;

tgx=2tgx21−tg2x2x=+2nnZx=2+nnZ;

ctgx=2tgx21−tg2x2x=nnZx=+2nnZ.

38. Определенные интегралы (интеграл Римана).

     Пусть действительная функция f(x) определена и ограничена на ограниченном замкнутом интервале [a, b]. Разобъем этот интервал на n частичных интервалов точками

a = x₀ < x₁ < x₂ < ... < x_n = b.

Выберем в каждом из частичных интервалов по произвольной точке и составим сумму (интегральная сумма).

     Если существует предел интегральной суммы при стремлении к нулю длины наибольшего частичного интервала разбиения: , то функцияf(x) называется интегрируемой в смысле Римана на интервале [a, b]. Предел этой суммы

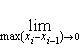
называется определенным интегралом от f(x) по интервалу [a, b] в смысле Римана (интеграл Римана). Это определение означает, что для любого положительного числа существует такое число, что при любом разбиении интервала [a, b] на частичные интервалы, длины которых меньше .

и при любом выборе промежуточных точек выполняется неравенство

     Функция f(x) называется подынтегральной функцией, а a и b - пределами интегрирования.

ТЕОРЕМА 1. ( необходимое условие существования интеграла) Если существует интеграл Римана , то функцияограничена на отрезке.

39.  Оценки интегралов

     1. Если то

     2.

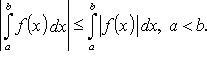
     3. Если то