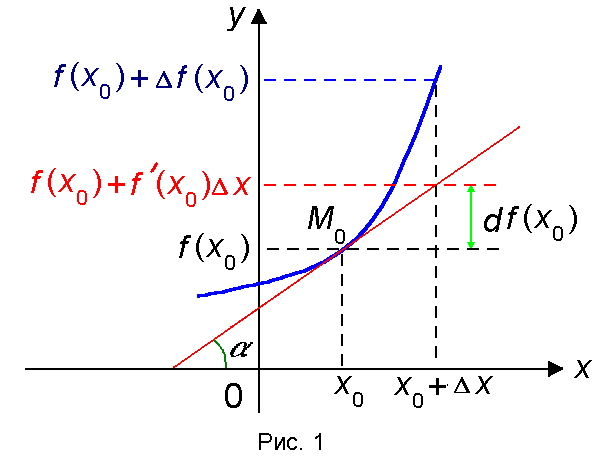Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТАН.docx

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.45 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

1/ Множеством называется совокупность элементов, объединенных каким-либо свойством.

Обозначается множество заглавными латинскими буквами, элементы множества – малыми, например запись

означает, что множество образовано элементами, обладающими свойством.

Если все элементы множества являются элементами множества, и не все элементы множестваявляются элементами множества, то множествоназываетсяподмножеством множества , обозначается.

Множество, подмножествами которого являются все рассматриваемые множества, называется универсумом. В качестве универсума в первом семестре будем рассматривать множество действительных чисел .

Элемент называетсянаибольшим (наименьшим) элементом множества , есливыполняется().

Элемент называетсяверхней (нижней) гранью множества , есливыполняется(). Если множество имеет верхнюю и нижнюю грани, оно являетсяограниченным. Наименьшая из верхних граней множества называется точной верхней гранью, обозначается . Наибольшая из нижних граней множества называетсяточной нижней гранью, обозначается .

Свойство ограниченного множества:

Всякое непустое ограниченное множество имеет точные верхнюю и нижнюю грани.

Свойство точных граней.

Если , то, т.е. точная верхняя грань не уменьшаема.

2/Определение. Функция называетсяпоследовательностью, значения функции

, где

называются членами последовательности.

Последовательность обозначают .

Определение. Последовательность называетсябесконечно большой, если для любого сколь угодно малого числа найдется номер, такой, что для всех элементов последовательности с номерами большимивыполнено неравенство

Или кратко:

Определение. Последовательность называется ограниченной, если найдется число , такое что для всех членов последовательности выполняется неравенство

Если такого числа подобрать нельзя, то последовательность называется неограниченной.

Теорема о неограниченности бесконечно большой последовательности. Всякая бесконечно большая последовательность является неограниченной.

3/Определение. Последовательность называетсябесконечно малой, если для любого сколь угодно малого числа найдется номер, такой, что для всех элементов последовательности с номерами большимивыполнено неравенство. Или кратко:

Теорема. Бесконечно малая последовательность является ограниченной.

Теорема. Последовательность является бесконечно большой тогда и только тогда, когда последовательностьявляется бесконечно малой.

Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Разница двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.

4/ Пределом последовательности вещественных чиселназывается число, если выполнено следующее условие:

то есть для любой окрестности точки можно указать номер, начиная с которого все элементы последовательности будут лежать в этой окрестности. Также можно дать эквивалентное определение: числоназывается пределом последовательности, если в любой его окрестности содержится бесконечное число элементов последовательности, а вне этой окрестности — лишь конечное число. Таким образом, пределом последовательности может быть толькопредельная точкамножества её элементов. Это определение согласуется с общим определением предела для топологических пространств.

Если последовательность имеет предел, то она называется сходящейсяк числу, если нет, торасходящейся. Тот факт, что числоявляется пределом последовательности, записывается следующим образом:

Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании.

5/ Теорема об арифметике пределов последовательностей.

Пусть и, тогда:

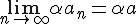для любого действительного числа ;
;
;
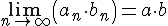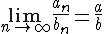, если .

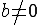6\Теоремы о предельном переходе.

1. Пусть – сходящаяся последовательность, и существует число , такое, что для всех элементов последовательности, начиная с некоторого, выполняется неравенство(), тогда().

2. Если начиная с некоторого номера, элементы сходящихся последовательностей иудовлетворяют неравенству, то.

3. Теорема о двух милиционерах. Пусть , и для всех элементов последовательностей, начиная с некоторого, выполняются неравенства

тогда .

7/ Определение. Последовательность

называетсямонотонной, если ее элементы удовлетворяют одному из следующих неравенств:

, .

В первом случае последовательность называется монотонно возрастающей, во втором – монотонно убывающей.

Теорема (критерий Вейерштрасса): Всякая монотонная ограниченная последовательность сходится.

Определение. Пусть

и ,

тогда последовательность отрезков называетсясистемой вложенных отрезков.

Определение. Последовательность называетсяфундаментальной, если .

Теорема (центральная предельная теорема Коши): Последовательность сходится тогда и только тогда, когда она фундаментальна.

8/Теорема (второй замечательный предел). .

Д о к а з а т е л ь с т в о: Прежде докажем вспомогательное утверждение.

Лемма. Для любого имеет место неравенство.

9/Предел функции в точке

Пусть функция , точка– предельная точка множества.

Определение. (По Гейне) Число называетсяпределом функции в точке, если для любой сходящейся кпоследовательности() последовательностьсходится к числу.

Определение. (По Коши) Число называетсяпределом функции в точке, если

обозначается

Теорема. Определения по Коши и по Гейне эквивалентны.

Эквивалентность определений означает, что из одного определения следует другое и наоборот.

Определение. Число () называетсяправым (левым) пределом функции в точке, если

().

Обозначаются

().

Теорема. Функция имеет предел в точкетогда и только тогда, когда в этой точке существуют конечные правый и левый пределы этой функции и эти пределы равны:

10. Теорема. (единственности). Если предел функции в точке существует, то он единственен.

Д о к а з а т е л ь с т в о. По определению предела функции по Гейне

Так как предел последовательности единственен, то единственно число . Теорема доказана.

Теорема (об арифметике). Пусть и, тогда верны следующие утверждения

.
.
.
, если .

Теорема (о предельном переходе в неравенствах) Пусть и имеют место неравенства

тогда существует и этот предел равен.

Д о к а з а т е л ь с т в о. Так как , то по определению по Гейнедля любой сходящейся кпоследовательности. Кроме того,. По теореме о предельном переходе для последовательностей последовательность сходится и, что означает, что. Теорема доказана.

11.Первый замечательный предел

12. Второй замечательный предел для функций

Вопрос 13 (экзаменационный)

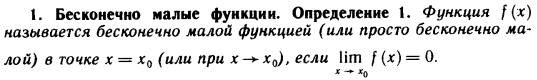
теорема о вычислении пределов с помощью эквивалентностей) Критерий эквивалентности

Доказательство. (необходимость) Пусть, т.е. по определению, тогда, гдеприи

(достаточность)

Пусть , тогда, т.е..

Непрерывные в точке функции

Определение. Пусть функция определена в точкеи некоторой ее окрестности,называетсянепрерывной в точке , если

Так как по критерию существования предела существует тогда и только тогда, когда существуют, конечны и равны между собой односторонние пределы функции в точке, то определение непрерывной в точке функции равносильно одновременному выполнению следующихусловий:

1) существует ; 2)и; 3).

Определение. Если в точке условия 1) – 3) не выполняются, тоназываетсяточкой разрыва функции . В зависимости от того, какие из условий 1) – 3) не выполнены, точки разрыва разделяют на два вида:точки разрыва I-го рода – если и, при этом:

если , то– устранимая точка разрыва;

если , то– точка разрыва типа «скачок».

точки разрыва II-го рода – если хотя бы один из пределов иявляется бесконечным.

Локальная ограниченность. Если непрерывна в точке, тоограничена в некоторой окрестности этой точки. Так как непрерывная в точке функция имеет конечный предел в этой точке, то из свойства локальной ограниченности функции, имеющей конечный предел в точке, следует локальная ограниченность непрерывной функции.Сохранение знака. Если непрерывна в точкеи, то для всехиз некоторой окрестности этой точки

(то есть иодного знака).

15. Определение. Функция, непрерывная в каждой точке некоторого множества называется непрерывной на этом множестве. Класс непрерывных на множестве обозначается, записьозначает, что– непрерывная нафункция.

1. Теорема Больцано-Коши 1. Пусть и(принимает на концах отрезка значения разных знаков), тогда.

2. Теорема Больцано-Коши 2. Пусть и,, тогда.

16. Теорема Вейерштрасса 1. Пусть , тогдаограничена на(т.е.).

4. Теорема Вейерштрасса 2. Если , то. (то есть непрерывная на отрезке функция достигает на этом отрезке своих наименьшего и наибольшего значений).

Замечания.

1. Точки, в которых непрерывная на отрезке функция достигает наибольшего и наименьшего значения, могут быть как внутренними точками отрезка, так и граничными.

2. Если , то

–наименьшее значение и

–наибольшее значение функции на отрезке.

Если , то может оказаться, чтоине достигаются на интервале, значитине существуют.

17. Теорема об арифметике. Если и– непрерывные в точкефункции, тогда функции,,,(при условии, что) также непрерывны в точке.

Теорема о сложной функции. Пусть функция , и, и для любогонайдется, такой что. Пустьи функциянепрерывна в точке, а функциянепрерывна в точке, тогда сложная функциянепрерывна в точке.

18. Пусть -- непрерывная монотонная функция,,. Тогда обратная кфункциянепрерывна на отрезке.

Производная функции

Определение. Пусть функция определена в точкеи некоторой ее окрестности. Зададим приращениетак, чтобы точкапринадлежала этой окрестности. Если существуют и конечны пределы

и ,

то их называют соответственно производной справа и слева в точке .Теорема. Функция имеет конечную производную в точкетогда и только тогда, когдаисуществуют, конечны и равны между собой.

Дифференцируемая функция

Определение. Пусть функция определена в точкеи некоторой ее окрестности. Зададим приращениетак, чтобы точкапринадлежала этой окрестности. Этому приращению соответствует приращение функции. Если существует число, такое что приращение функции можно представить в виде:

где при, то функцияназываетсядифференцируемой в точке . Так как, при, то условие дифференцируемости можно записать в виде:

Теорема (необходимое условие дифференцируемости) Если функция дифференцируема в точке, то она непрерывна в этой точке.

Теорема (необходимое и достаточное условия дифференцируемости). Функция дифференцируема в точке тогда и только тогда, когда она имеет конечную производную в этой точке.

Замечание. Из теоремы следует, что понятия производная и дифференцируемость эквивалентны, и в силу того, что при доказательстве получили , условие дифференцируемости имеет вид:

Теорема об арифметике дифференцируемых функций

Теорема. Если функции идифференцируемы в точке, то функции, где,,и(при условии что) дифференцируемы в точке. При этом

а) б) в) . г) .

Теорема о производной сложной функции

Теорема. Пусть ,и для любогонайдется элемент, такой, что, тогда на множествеможно определить сложную функциюсо значениями в. Если функциядифференцируема в точке, а функциядифференцируема в точке, то сложная функциядифференцируема в точке. При этом производная сложной функции находится по формуле:

Теорема. Если функция дифференцируема в точкеи, то обратная функциядифференцируема в точкеи ее производная равна:

или кратко .

Пусть функция y = f(x) определена в некоторой окрестности точки x0.

Функция f(x) называется дифференцируемой в точке х0, если ее приращение представимо в виде

Δf = f(x0 + Δx) − f(x0) = A · Δx + o(Δx) ,

где A — число, не зависящее от Δх, а o(Δx) — функция более высокого порядка малости чем Δx при Δх → 0 .

Таким образом, приращение дифференцируемой функции является суммой линейной относительно Δx ч асти A · Δx и бесконечно малой более высокого порядка малости чем Δx при Δх → 0.

Линейная часть приращения дифференцируемой функции называется дифференциалом в точке х0 и обозначается символом df(x0), т.е.

df(x0) = A · Δx.

Геометрический смысл дифференциала

Пусть функция f(x) дифференцируема в точке х0. Проведем касательную к графику этой функции в точке M0(x0, f(x0)) (рис. 1).

Угловой коэффициент касательной равен tg α = f '(x0), где α — угол между касательной и осью OX. При изменении абсциссы х0 на Δx приращение ординаты соответствующей точки касательной равно

Δx · tg α = f '(x0) · Δx ≡ df(x0).

Таким образом, дифференциал функции f(x) в точке х0 равен приращению, которое получает линейная функция, графиком которой является касательная, при переходе из точки x0 в точку x0 + Δx.

Определим геометрический смысл производной.

На кривой графика функции отметим точки и, соединим эти точки отрезком прямой, получим секущую графика функции.

Теорема Ферма (необходимое условие локального экстремума) Определение. Пусть функция определена на множествеи. Точканазывается точкой локального экстремума функции, если найдется некоторая окрестность, для всех точек которой выполняется одно из следующих условий:

––точка локального максимума; –– точка локального минимума;–– точка строгого локального максимума;–– точка строгого локального минимума.

Теорема. Если – точка локального экстремума дифференцируемой функции, то.

Терема Ролля. Если непрерывна на, дифференцируема наи, то найдется точка, в которой.

24. Теорема Лагранжа. Если непрерывна на, дифференцируема на, то найдется точка, такая что.

Теорема Коши. Пусть функции инепрерывны наи дифференцируемы на, причем. Тогда

25. Теорема Лопиталя (о раскрытии неопределенностей). Пусть функции и

1) дифференцируемы в (над окрестностью означает, что в точкефункции могут и не иметь производных) и; 2) ; 3) существует предел ,

тогда и .

29,30.

31. Достаточный признак монотонности дифференцируемой функции: если на интервалех(а,b) производнаясохраняет знак, то функциясохраняет монотонность на этом интервале, а именно: если, тоf(x) возрастает, если, тоf(x) убывает.

^ Необходимое условие существования экстремума функции: если непрерывная функцияимеет экстремум в точкех₀, то ее производная в этой точке равна нулю или не существует. Точки, принадлежащие ООФ, в которых производнаяравна нулю или не существует, называюткритическими точками функции по ее первой производной (точками, «подозрительными на экстремум»).^ Первый достаточный признак существования экстремума: если при переходе через критическую точкух₀(слева направо) производнаяизменяет свой знак, то в точкех₀есть экстремум причем это максимум, если знакменяется с плюса на минус, и это минимум, если знакменяется с минуса на плюс. Если при переходе через критическую точкух₀производнаяне изменяет свой знак, то в точкех₀нет экстремума функции.Второй достаточный признак существования экстремума: если– дважды дифференцируемая функция в точкех₀и, тогда: если, тох₀– точка минимума функции, а если, тох₀– точка максимума. Для нахождения точек экстремумов функциисначала находят критические точки по первой производной. После этого проверяют выполнение в них достаточных условий существования экстремума функции.

32. Достаточное условие выпуклости, вогнутости графика функции: если функцияявляется дважды дифференцируемой и ее вторая производнаясохраняет знак при всехx(a;b), то график функции имеет постоянное направление выпуклости на этом интервале: при<0 – выпуклость вверх, при>0 – вогнутость (выпуклость вниз).^ Необходимое условие для точки перегиба: еслих₀– абсцисса точки перегиба графика функции, то ее вторая производная в этой точке равна нулю или не существует. Точки, принадлежащие графику функции, в которыхилине существует, называютсякритическими точками функции по ее второй производной (точками, «подозрительными на перегиб»).^ Достаточное условие для точек перегиба: если вторая производнаяпри переходе через точкух₀, подозрительную на перегиб, изменяет знак, то точка графика с абсциссойх₀является точкой перегиба. Еслине изменяет знак при переходе через точкух₀, то перегиба нет. При нахождении промежутков выпуклости, вогнутости графика функциисначала находят критические точки по второй производной, после этого выделяют промежутки знакопостоянства второй производной на ООФ: если, то кривая вогнутая, а если, то кривая выпуклая. Точки перегиба определяют, используя достаточные условия перегиба.