4. Пример расчета на основе линейной модели.

Условие задачи: Для расчетной схемы, представленной на рис. 2.5 записать матричное уравнение узловых напряжений и рассчитать значения узловых напряжений методом Гаусса.

Исходные данные:

- сопротивления

ветвей;

- задающие токи, моделирующие

подключение нагрузки.

Расчет начинается с формирования уравнения состояния по расчетной схеме:

1. С

   Номер ветви

   оставим матрицу инциденций 1-го рода.

1 2 3 4 5 6

При правильном составлении матрицы М строка, соответствующая балансирующему узлу, дополняет каждый столбец до нуля.

2.Составим транспонированную матрицу

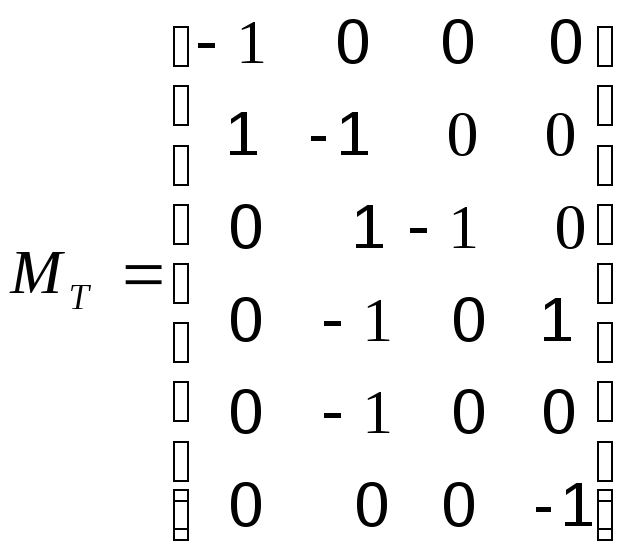
3.Определяем матрицу узловых проводимостей

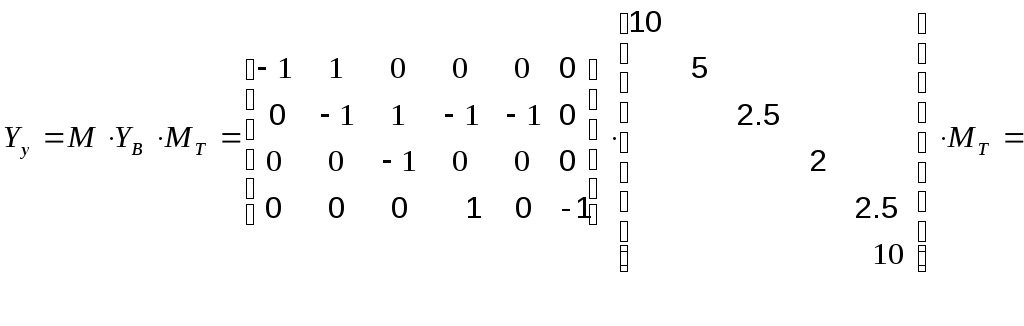
В матричной форме уравнение узловых напряжений имеет вид:

(2.5)

5. Перейдем к системе уравнений :

(2.6)

Далее, используя уравнения узловых напряжений, можно провести расчет установившегося режима в следующем порядке:

1. Решая систему уравнений вида (1.12), определяются значения узловых напряжений . Произведем расчет с помощью метода Гаусса.

Прямой ход Гаусса состоит из однотипных шагов, связанных с формированием из матрицы коэффициентов верхней треугольной матрицы.

Шаг 1. Получим первое ключевое уравнение, для чего разделим первое уравнение системы (2.5) на коэффициент при , а затем исключимиз всех уравнений, расположенных ниже ключевого.

(2.7)

Шаг 2. Принимаем за ключевое второе уравнение (разделим все коэффициенты на ) и исключимиз уравнений ниже ключевого.

Преобразованная система, начиная с ключевого уравнения имеет вид:

(2.8)

Шаг 3. Принимаем за ключевое третье уравнение и исключаем из всех уравнений ниже ключевого, преобразованная система, начиная с ключевого уравнения имеет вид:

(2.9)

Шаг 4. Выбираем четвертое ключевое уравнение:

(2.10)

Обратный ход Гаусса:

Анализ точности расчета: Производится расчет невязок по исходной системе уравнений:

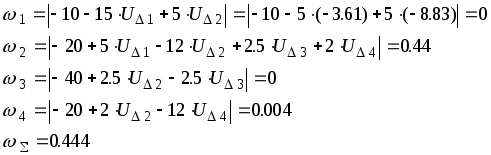(2.11)

2. Из уравнения связи параметров режима [ 1 ] находятся падения напряжений в ветвях

.(2.12)

3. Из уравнения закона Ома (1.1) определяются токи в ветвях схемы

. (2.13)

4.По известным значениям иопределяются остальные параметры режимаи т.д.

2.5 Реализация расчета режима в среде Mathcad.

Возможности математического пакета программ Mathcad PLUS 6.0 позволяют реализовать расчет установившегося режима на основе уравнений состояния, представленных в матричной форме.

Расчетная схема содержит 7 узлов и 10 ветвей :

Приведем пример реализации расчета на основе обобщенного уравнения состояния и уравнений узловых напряжений, который положен в основу лабораторных работы по курсу.

Лабораторная работа N 1

Тема: Обобщенное уравнение состояния. Расчет токов в ветвях схемы электрической системы.

Матрица инцидений 1-го рода

Матрица инциденций 2-го рода

Сопротивления ветвей

Произведение матриц

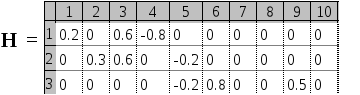
Матрица коэффициентов

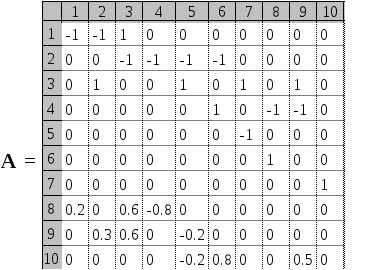
Расчет токов в ветвях схемы.

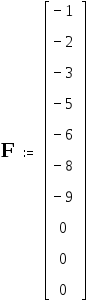
токи в ветвях

Токи равны:

Лабораторная работа N 2

Тема: Уравнения узловых напряжений. Расчет узловых напряжений

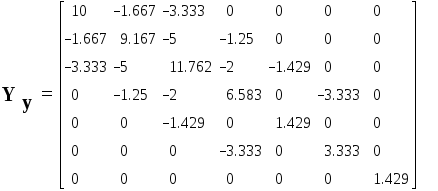
Матрица узловых проводимостей :

_{Матрица проводимостей ветвей схемы и вектор задающих токов:}

Вектор узловых напряжений :

Вектор падений напряжений в ветвях :

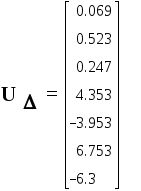
_{- узловые напряжения}

Токи в ветвях:

6. _{Задание № 1 по контрольной работе.}

Задана расчетная схема электрической системы, представленная в виде направленного графа, который содержит 5 узлов, 7 ветвей и 2 независимых контура (по вариантам в приложении 1). Направление ветвей и независимых контуров может быть задано произвольно. Для указанной схемы ЭС необходимо рассчитать параметры установившегося режима. В связи с этим, требуется выполнить следующие пункты задания: 1.Составить обобщенное уравнение состояния на основе первого и второго законов Кирхгофа, записать этого уравнение в матричной форме и в виде системы уравнений;

2.Вычислить матрицу узловых проводимостей и записать уравнение узловых напряжений в матричной форме и в виде системы уравнений;

3. Рассчитать узловые напряжения и токи в ветвях с использованием метода Гаусса с обратным ходом. Оценить точность полученных результатов. Исходные данные, необходимые для проведения расчетов, приведены в таблице 1 приложения