3.2. Многофакторные мультипликативные модели Решение типовой задачи (на примере трехфакторной модели)

Условие: определить влияние численности персонала, количества отработанных смен и выработки в смену на одного работника на изменение объема выпуска продукции (N_п).

Месяцы	Численность работников, чел.	Выработка в смену, шт.	Количество смен
1	24	1500	144
2	25	1505	146

Сделать вывод.

Алгоритм решения:

1. Факторная модель, описывающая взаимосвязь показателей, имеет вид: N = ч * См * В

2. Исходные данные – факторы и результирующий показатель представляются в аналитической таблице:

Показатели	Условные обозначения	Базисный период	Отчетный период	Отклонение	Темп изменения, %
1. Численность работников, чел.	ч	24	25	+1	104,2
2. Количество смен	См	144	146	+2	101,4
3. Выработка, штук	В	1500	1505	+5	100,3
4. Выпуск продукции, тыс. шт.	N	5184	5493,25	+309,25	106,0

3. Способы детерминированного факторного анализа, применяемые для решения трехфакторных моделей:

 цепной подстановки;

 абсолютных разниц;

 взвешенных конечных разниц;

 логарифмический;

 интегральный.

4. Применение различных методов для решения типовой задачи:

   1. Способ цепной подстановки. Применение этого способа предполагает выделение количественных и качественных факторных признаков: здесь количественными факторами являются численность персонала и количество отработанных смен; качественный признак – выработка.

а) N₁ = ч₀ * См⁰ * В⁰ =5184 тыс. шт.;

б) N₂ = ч¹ * См⁰ * В⁰ =25 * 144 * 1500 =5400 тыс. шт.;

в) N (ч) = 5400 – 5184 = 216 тыс. шт.;

N₃ = ч¹ * См¹ * В⁰ =25 * 146 * 1500 =5475 тыс. шт.;

N(См) = 5475 – 5400 = 75 тыс. шт.;

N₄ = ч¹ * См¹ * В¹ =25 * 146 * 1505 =5493,25 тыс. шт.;

N(В) = 5493,25 – 5475 = 18,25 тыс. шт.;

N =N(ч) +N(См) +N (B) = 216 + 75 +18,25 = 309,25 тыс. шт.

4.2. Способ абсолютных разниц также предполагает выделение количественных и качественных факторов, определяющих последовательность подстановки:

а) N(ч) =ч * См⁰ * В⁰ = 1 * 14 * 1500 = 216 тыс. шт.;

б) N(См) =См * ч¹ * В⁰ = +2 * 25 * 1500 = 75 тыс. шт.;

в) N (B) =B * ч¹ * См¹ = +5 * 25 * 146 = 18,25 тыс. шт.;

N = N(ч) +N(См) +N (B) = 309,25 тыс. шт.

3. Способ относительных разниц

а) N(ч) =тыс. шт.;

б) N(См) =тыс. шт.;

в) N(В)тыс. шт.;

Общее влияние факторов : N =N(ч) +N(См) +N (B) = 309,3 тыс. шт.

4.4. Способ взвешенных конечных разностей предполагает применение всех возможных постановок на основе способа абсолютных разниц.

Подстановка 1 производится в последовательности результаты определены в предыдущих расчетах:

N(ч) = 216 тыс. шт.;

N(См) = 75 тыс. шт.;

N (B) = 18,25 тыс. шт.

Подстановка 2 производится в последовательности :

а)+1 * 1500 * 144 = 216 тыс. шт.;

б) +5 * 25 * 11 = 18 тыс. шт.;

в) +2 * 25 *1505 = 75,5 тыс. шт.;

Подстановка 3 производится в последовательности :

а) 2 * 24 * 1500 = 72 тыс. шт.;

б) 1 * 146 * 1500 = 219 тыс. шт.;

в) + 5 * 25 * 146 = 18,25 тыс. шт.

Подстановка 4 производится в последовательности :

а) 2 * 1500 *5 * 146 * 24 = 17,52 тыс. шт.;

б) 5 * 146 * 24 = 17,52 тыс. шт.;

в) 1 * 146 * 1515 = 219,73 тыс. шт.;

Подстановка 5 производится в последовательности :

а) 5 * 144 * 24 = 17,28 тыс. шт.;

б) 2 * 1505 * 24 = 72,27 тыс. шт.;

в) 1 * 146 * 1505 = 219,73 тыс. шт.

Подстановка 6 производится в последовательности :

а) 5 * 24 * 144 = 17,28 тыс. шт.;

б) 1 * 1505 * 144 = 216,72 тыс. шт.;

в) 2 * 1505 * 25 = 75,25 тыс. шт.

Влияние факторов на результирующий показатель

Факторы	Размер влияния факторов при подстановке, тыс. шт.						Среднее значение влияния факторов
	№ 1	№ 2	№ 3	№ 4	№ 5	№ 6
1. Численность	216	219	216	219,73	219,73	216,72	217,86
2. Сменность	75	72	75,25	72	72,27	75,25	73,63
3. Выработка	18,25	18,25	18,0	17,52	17,28	17,28	17,76
4. Итого:	309,25	309,25	309,25	309,25	309,25	309,25	309,25

4.5. Логарифмический способ предполагает распределение отклонения результирующего показателя пропорционально доле каждого фактора в сумме отклонения результата

а) доля влияния каждого фактора измеряется соответствующими коэффициентами:

б) влияние каждого фактора на результирующий показатель рассчитывается как произведение отклонения результата на соответствующий коэффициент:

309,25*0,706 = 218,33;

309,25*0,2438 = 73,60;

309,25* 0,056 = 17,32.

4.6. Интегральный метод предполагает применение стандартных формул для расчета влияния каждого фактора:

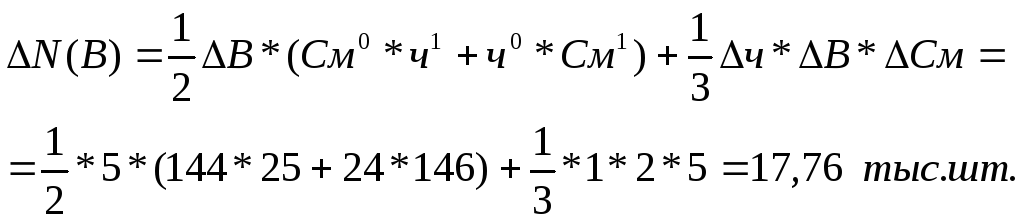
5. Результаты расчетов каждого из перечисленных способов объединяются в таблице совокупного влияния факторов.

Совокупное влияние факторов:

Факторы	Размер влияния, тыс. шт.		Способом относительных разниц	Размер влияния, тыс. шт.
	Способом цепных подстановок	Способом абсолютных разниц		Способом взвешенных конечных разниц	Логарифм. способ	Интегральный способ
1. Численность	216	216	216,17	217,86	218,33	217,86
2. Количество смен	75	75	75,06	73,63	73,60	73,63
3. Выработка	18,25	18,25	18,07	17,76	17,32	17,76
4. Итого:	309,25	309,25	309,3	309,25	309,25	309,25

Сопоставление результатов расчетов, полученных различными способами (логарифмическим, интегральным и взвешенных конечных разниц), показывает их равенство. Громоздкие расчеты способом взвешенных конечных разниц удобно заменить применением логарифмического и интегрального методов, которые дают более точные результаты по сравнению с приемами цепной подстановки и абсолютных разниц.

5. Вывод: Объем выпуска продукции возрос на 309,25 тыс. штук.

Положительное влияние в размере 217,86 тыс. шт. оказал рост численности персонала.

В результате увеличения количества смен объем выпуска возрос на 73,6 тыс. шт.

За счет увеличения выработки объем выпуска продукции увеличился на 17,76 тыс. шт.

Наиболее сильное влияние на объем выпуска продукции оказали экстенсивные факторы: рост численности персонала и количества отработанных смен. Совокупное влияние этих факторов составили 94,26 % (70,45 +23,81). На долю влияния фактора выработки приходится 5,74 % роста выпуска продукции.

По результатам анализа можно рекомендовать предприятию разработать ряд мер, по повышению производительности труда, что при неизменности экстенсивных фактора работы приведет к повышению прибыли.

Примечание: Применение рассмотренных приемов аналогично в отношении мультипликативных моделей любого количества факторов. Однако использование приема взвешенных конечных разниц к многофакторным моделям ограничено необходимостью выполнения большого количества расчетов, и это нецелесообразно при наличии других, более простых и рациональных приемов, например, логарифмического.