Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новгородский Государственный Университет им. Ярослава Мудрого

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метод-ка ВМ для ст.зу.Ч.2 к.р. 3,4

..pdf

Скачиваний:

Добавлен:

26.03.2015

Размер:

2.75 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

По свойству аддитивности поверхностного интеграла первого рода получаем

x2 dS

= x2 dS x2 dS

= 2 x2

dxdy =

2 x2

dxdy (перейдѐм в интеграле к полярным координа-

a2 x2 y2

r 2 cos2 r

r3dr

там) = 2 a

dr = 2a

cos2 d

= (так как инте-

a2 r 2

2	2	1 cos2			2	a	r	3	dr
грал cos2 d			d 1	1 sin 2	\|	) = 2a				=

0	0	2	2	4	0	0	a2 r 2

(произведѐм

r 2 a2 t 2 ) =

замену

переменной t

a2 r 2 , t 2 a2 r 2 , rdr tdt ,

)(t)dt

2a a

2t t3

a4 .

Поверхностный интеграл второго рода

Если в каждой точке области V пространства R3 определена вектор

–функция F(x, y, z) P(x, y, z)i Q(x.y, z) j R(x, y, z)k , тогда говорят, что

вобласти V задано векторное поле F .

Пусть поверхность S V , тогда поверхностный интеграл (F n) dS ,

где n – единичный вектор нормали к поверхности S в точке (x, y, z) S , F n – скалярное произведение векторов F и n , называют потоком векторного поля F через поверхность S в направлении нормали n . Отметим, что поток в противоположном направлении имеет противоположный знак(F (n))dS (F n) dS . Поверхностный интеграл второго рода мож-

S S

но вычислять двумя способами.

1). Если поверхность S задана уравнением f (x, y, z) 0 , тогда вектор

)

из частных производных grad f (M

) k ,

который называется градиентом функции f

, является нормалью к поверх-

ности S в точке M0 (x0 , y0 , z0 ) S (при этом

f (x0 , y0 , z0 ) 0). Тогда вектор

	grad f (x, y, z)
единичной нормали n	grad f (x, y, z)	, а скалярное произведение (F n)
единичной нормали n	\| grad f \|	, а скалярное произведение (F n)
	\| grad f \|

			21
Pf / Qf / Rf /
x	y	z		. Подставив полученное выражение для скалярного

( f / )2	( f / )2	( f / )2
x	y	z

произведения в интеграл, получим поверхностный интеграл первого рода.

Вычислить поток векторного поля

че-

Пример.

рез полную поверхность сферы x2 y2 z2 a2

в направлении внешней

нормали.

Градиент

функции f (x, y, z) x2 y2 z2

a2 равен

grad f

2xi 2 y j 2zk

и является внешней нормалью к сфере. Вектор единичной

grad f (x, y, z)

xi y j zk

нормали

. Следовательно,

(F n) dS =

| grad f |

x2 y2

z 2

4 y4 z

dS =

x4dS

y4dS

z 4dS

x2 y2 z 2

x2 y2 z2

x2 y2 z 2

2 y2 z 2

Вычислим первый интеграл. Как в предыдущем примере разобьѐм

сферу

на

две

полусферы

S и

S ,

уравнения

которых

a dxdy

a2 x2 y2 соответственно,

Имеем

2 x2 y2

x4dS

y2 z 2

x4dS

= 2

dxdy , так как на

x2 y2 z 2

a2 x2 y2

сфере S будет

x2 y2

z2 a , круг K : x2

y2 a2 – проекция полусфер

S и S

на координатную плоскость

XOY .

Переходя в последнем инте-

грале

полярным

координатам,

получим

dxdy

a2 x2 y2

2 cos4 d

= (произведѐм во

внутреннем

интеграле

замену

a2 r 2

1 cos2 2

, rdr tdt ,

)

d (a

)

1 2cos2 cos2 2 d (a4 2a2t 2

t 4 )dt

= 4

, так как внутрен-

ний интеграл (a4 2a2t 2 t 4 )dt

= a4t 2 a2t3

1 t5

a5 , а интеграл

2 d =

2cos2

cos4

1 2cos2 cos

d 3 .

Второй интеграл вычисляется аналогично и равен также

4 a5 .

Вычислим

третий

интеграл:

z 4dS

x2 y2 z 2

z 2

z 4dS

= 2

x2 y2

dxdy

(так

как на

x2 y2 z 2

a2 x2

z a2 x2

y2 , а

a2 x2

x2 y2

и инте-

равны) = 2

3 dxdy = (переходим к поляр-

гралы по S и S

54 a5 . Сложив по-

ным координатам) = 2

r 2

dr = 4

t 4dt

лученные значения всех трѐх интегралов, получим, что искомый поток ра-

вен 54 a5 + 54 a5 + 54 a5 = 125 a5 .

2). Пусть поверхность S однозначно проектируется на координатные плоскости YOZ, XOZ, XOY , вектор единичной нормали n (cos,cos ,

cos ) , где , , – углы, которые вектор n образует с координатными осями OX, OY, OZ соответственно. Тогда (F n) dS = P(x, y, z)cos dS +

		S	S
Q(x, y, z)cos dS + R(x, y, z)cos dS = P(x( y, z), y, z) dydz
S	S		S yz
Q(x, y(x, z), z) dxdz		R(x, y, z(x, y))dxdy , где знак + перед интегралом
Sxz		Sxy

ставится в том случае, если соответствующий угол острый, а знак – ставится в том случае, если соответствующий угол тупой (если угол равен

900 , тогда косинус этого угла равен 0, а значит, равен 0 и соответствующий интеграл); функции x( y, z) , y(x, z), z(x, y) находят из уравнения по-

верхности S. Если поверхность S не однозначно проектируется на какую либо координатную плоскость, тогда еѐ разбивают на части, каждая из которых однозначно проектируется на эту плоскость, а затем используют свойство аддитивности интеграла.

Пример. Вычислить поток векторного поля

че-

рез полную поверхность сферы

x2 y2

a2 в направлении внешней

нормали.

Имеем,

(

) dS = x3 cos dS + y3 cos dS

+ z3 cos dS . Вы-

числим первый интеграл. Сфера S не однозначно проектируется на плос-

кость YOZ, поэтому разобьѐм еѐ на две полусферы S и S , уравнения ко-

торых

a2 y2 z2 .

Тогда, по свойству аддитивности интеграла,

3 dydz –

x3 cos dS =

x3 cos dS

a2 y2

z 2

3 dydz

3 dydz ,

a2 y2 z 2

a2 y2

z 2

где

круг

K : y2 z2 a2 – проекция полусфер S

и S

на координатную плоскость

YOZ . При этом интеграл по S берѐтся со знаком +, а интеграл по

S со

знаком –, так как вектор нормали n на полусфере S образует острый угол с осью OX, а на полусфере S – тупой угол. Перейдя в последнем интегра-

ле

к полярным

координатам:

y r cos , z r sin,

получим

a2 y2

z 2 dydz

= 2

d r

r 2 dr = 4 r a2 r 2

dr (сде-

лаем замену t

r 2 , t2 a2 r2 , tdt rdr ) =

4 t 3t dt = 54 a5 . Сле-

довательно, x3 cos dS

= 54 a5 . Второй и третий интегралы вычисляются

также как первый и равны

4 a5 .

Сложив все три интеграла,

получим

(F n) dS =

Формула Гаусса – Остроградского

Задание 4.

Определение. Дивергенцией (расходимостью) векторного поля F в

точке M (x, y, z) называют

предел

отношения потока векторного поля

F через замкнутую поверхность SM , окружающую

точку M, в направле-

нии внешней нормали к объѐму тела VM , ограниченного этой поверхно-

стью, при VM 0 .

Дивергенция векторного поля F обозначается div F и

вычисляется по формуле: div

(M ) Q (M )

R (M ) .

Векторное поле F называется соленоидальным, если div F 0.

Будем предполагать, что функции P(x, y, z), Q(x.y, z), R(x, y, z) и их

P Q R

частные производные первого порядка x , y , z непрерывны.

Пусть замкнутая поверхность S является границей ограниченной области VS пространства R3 . Тогда поток векторного поля F через поверх-

ность S в направлении внешней нормали определяется формулой Гаусса – Остроградского

(F n) dS divFdxdydz .

S VS

Из этой формулы следует, что в соленоидальном поле поток этого поля через замкнутую поверхность равен 0.

Пример. Вычислить, пользуясь формулой Гаусса – Остроградского, поток векторного поля F x3 i y3 j z3 k через полную поверхность сферы x2 y2 z2 a2 в направлении внешней нормали.

3x2

3y2

3z2 , а

Имеем div F

(F n) dS =

3 (x2 y2 z 2 ) dxdydz ,

где VS – шар x2 y2

z2 a2 . Для вычисления

полученного интеграла перейдѐм от декартовых координат к сферическим

координатам r, , :

x r sin cos , y r sin sin, z r cos ,

где r = 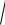x2 y2 z2 – расстояние от точки M (x, y, x) до начала координат, – угол, который радиус – вектор OM точки M образует с осью OZ,– угол, который радиус – вектор OM1 точки M1 (точка M1 является проекцией точки M на плоскость XOY) образует с осью OX. При этом, определитель Якоби I (r, , ) r 2 sin .

	В сферических координатах получим 3 (x2								y2 z 2 ) dxdydz =
								VS
2		a	4		a5	12	5
3	d sin d r		4	dr = 6 2	a5	12	5
3	d sin d r			dr = 6 2	5	5 a		.
0	0	0
					Формула Стокса

	Будем предполагать,				что векторное поле F				дифференцируемо, то

есть функции P(x, y, z), Q(x.y, z), R(x, y, z) имеют непрерывные частные производные первого порядка.

Определение. Вихрем векторного поля F , обозначаемым rot F назы-

вают вектор

rot F

k .

Теорема Стокса.

Циркуляция векторного поле F по кусочно глад-

кому замкнутому контуру L равна потоку поля rot F через поверхность SL ,

ограниченную этим контуром:

(F d r) (rot F n)dS ,

L		SL
				R	Q
		(Pdx Qdy Rdz) =		R	z
или в координатной форме				y	z	cos +
или в координатной форме						cos +
	L		SL

P	R	cos		Q	P
				x			dS . При этом вектор единичной нормали
z	x		+		y	cos

n к поверхности SL должен быть направлен так, чтобы из конца вектора

n обход контура L казался осуществляемым против часовой стрелки (в положительном направлении).

Пример. Вычислить циркуляцию векторного поля F zi x j 2 yk по замкнутому контуру L, образованному сечением сферы x2 y2 z2 a2 плоскостью x y в положительном направлении отно-

сительно орта i .

Контур L является окружностью радиуса a, которая расположена в плоскости x y , а поверхностью SL , ограниченной этим замкнутым кон-

туром, является круг, ограниченный этой окружностью. Вихрь векторного поля rot F 2i j k , вектор единичной нормали к поверхности SL , относительно которого контур L обходится в положительном направлении,

rot

, скалярное произведение

. Следовательно, по

теореме

Стокса, искомая циркуляция

zdx xdy 2 ydz

dS =

(площадь круга радиуса r) =

Потенциал векторного поля

Задание 5. Определение. Векторное поле F Pi Q j Rk называет-

ся потенциальным, если существует функция u(x, y, z)

такая, что справед-

grad u

или в скалярной форме u P, u

Q, u R , а

ливо равенство

функция u(x, y, z) называется потенциалом этого векторного поля.

Необходимым и достаточным условием потенциальности гладкого в

односвязной области векторного поля F является равенство нулю вихря этого поля: rot F 0.

Потенциальные поля в области непрерывности потенциала обладают следующими важными свойствами.

Работа поля не зависит от пути из точки A в точку B и равна разности значений потенциала в этих точках, то есть, если L1, L2 – два различных пу-



ти из точки A в точку B, тогда (F d r)					(F d r) u(B) u( A) ;
L1					L2

Работа поля по любому замкнутому контуру равна нулю.

Пусть точка A(x0 , y0 , z0 ) – фиксированная, а точка B(x, y, z) – произ-

вольная точки области непрерывности потенциального поля F . Тогда потенциал этого поля можно вычислить по следующей формуле:

x	y	z
u(x, y, z) P(t, y0	, z0 )dt Q(x,t, z0 )dt R(x, y,t)dt .
x0	y0	z0

Пример. Убедиться в том, что векторное поле

y2 z 2

x2 z2

z 2

F =

x2 yz

xy 2 z

xyz

потенциально и найти его потенциал.

Убедимся сначала в том, что рассматриваемое поле потенциально.

Име-

z 2

x2 z 2

x2 z 2 y2

ем,

xyz

x2 y2

x2 z 2 y2

R Q

. Следовательно,

xzy

y2 z 2 x2

z 2 y2

Аналогично,

Следователь-

yx2 z 2

zx 2 y2

R Q

P R

Q P

но,

rot F

и поле F потенци-

ально.

Выбрав x0 1, y0

1, z0

1, находим потенциал u(x, y, z)

1dt

= t

| +

xyt

xt 1

1 2

– 3. Следовательно, потенциал u(x, y, z)

С .

Числовые ряды

Задание 6. Понятие числового ряда. Выражение вида

an или an

n 1

| = xt 1

xyz yzx

(3)

называют числовым рядом. Числовую последовательность an называют

общим членом числового ряда (3). Сумма первых n членов числового ряда называется n – той частичной суммой ряда и обозначается Sn . Таким обра-

зом, возникает последовательность частичных сумм ряда (3)

S1 a1 , S2 a1 a2 , , Sn a1 a2 an ,

Если существует предел частичных сумм S lim Sn , тогда гово-

рят, что ряд (3) сходится, а число S называют суммой этого ряда. Если же предел частичных сумм не существует или равен ∞, тогда говорят, что ряд

(3) расходится.

1 1n . Преобразуем общий

Пример. Рассмотрим числовой ряд

n 1

член этого ряда an

ln 1

1n ln

ln(n 1) ln n .

Тогда частичная

ln 2 ln1

+ ln 3 ln 2

сумма ряда

Sn a1 a2

an 1

an =

+ +

ln n ln(n 1) + ln(n 1) ln n

= ln(n 1) ,

так как все другие слагаемые

сократились в силу чередования знаков. Далее, lim

Sn = lim ln(n+1) = ∞,

а значит, рассматриваемый числовой ряд расходится.

Пример. Исследуем сходимость ряда

.Общий член этого

n 1 n(n

ряда можно представить в виде разности

следовательно,

n 1

a a

n 1

= 1

n 1

= 1–

. Таким образом,

lim

Sn =

lim

= 1 и

n 1

рассматриваемый ряд сходится, а его сумма равна 1.

Необходимый признак сходимости числового ряда

Если числовой ряд (3) сходится, тогда lim an 0.

Действительно, из сходимости ряда (3) следует существование

lim Sn S . Тогда lim an = lim

Sn Sn 1

lim

Sn lim Sn 1= S S = 0.

Из необходимого признака сходимости ряда следует достаточный

признак расходимости ряда: если lim an 0 , тогда ряд an расходится.

n 1

Пример.

Числовой

ряд

расходится

так

как

lim an =

3n 1

n 1

lim

0 .

n 3n 1

Свойства числовых рядов

Числовые ряды обладают следующими свойствами:

1) если ряд an/

получен из ряда (3) отбрасыванием конечного чис-

n 1

ла слагаемых, тогда эти ряды сходятся или расходятся одновременно;

ряды

an и

С an ,

где C 0 ,

сходятся или расходятся одно-

n 1

временно и справедливо равенство (Сan )

С an ;

n 1

3) если ряды

an и

bn сходятся, тогда сходятся ряды

n 1

bn =

и справедливы равенства an

an bn .

n 1

Проиллюстрируем свойство 1) –3) на следующем примере. Известно,

что ряд

qn 1 сходится,

если | q | 1, и его сумма равна

Следова-

n 1

1 2n

тельно, числовой ряд

сходится и справедливо равенство

n 1

1 n

2 n

1 n 1

2 n 1

1 1

2 1

2 =

3 1 2

n 1

3 n 1

Признаки сходимости положительных рядов

Ряды (3), у которых все члены являются положительными числами, an 0 , называются положительными рядами. Вначале рассмотрим призна-

ки сравнения положительных рядов.

1. Мажорантный признак сравнения.

Пусть даны два положительных ряда


(1) an ,	(2) bn .
n 1	n 1

Если для любых n N (начиная с номера N ) выполняется неравен-

ство

an bn ,

тогда из сходимости ряда (2) (большего ряда) следует сходимость ряда (1) (меньшего ряда), а из расходимости ряда (1) следует расходимость ряда

(2).

1n расходится. Дока-

Пример. Ранее было доказано, что ряд ln

n 1

жем расходимость гармонического ряда

Воспользуемся неравенст-

n 1 n

вом ln(1 x) x для любых

x 0 . Действительно,

рассмотрим функцию

f (x) x ln(1 x) .

Так как производная f / (x)

0 для

1 x

всех x 0,

то функция

f (x) монотонно возрастает на промежутке [0, ) ,

значит,

для

любых

x 0

выполняется

неравенство

f (x)

x ln(1 x) f (0) 0 .

Так

как

0 ,

то

выполнено

неравенство

ln 1

и, гармонический ряд расходится.

2. Предельный признак сравнения.

Пусть для общих членов рядов (1), (2) существует конечный предел

lim an k 0, тогда эти ряды сходятся или расходятся одновременно.

n bn

Для успешного использования признаков сравнения необходимо иметь в своѐм распоряжении набор числовых рядов, о которых известно сходятся они или расходятся. Поэтому к уже рассмотренным рядам доба-

	1
вим обобщѐнные гармонические ряды			,	которые сходятся, если p 1
вим обобщѐнные гармонические ряды		p	,	которые сходятся, если p 1
n 1 n
и расходятся, если p 1.
					3n 1
Пример. Исследуем сходимость ряда						. Сначала
Пример. Исследуем сходимость ряда					4n3 n 2	. Сначала
		n 1			4n3 n 2

установим асимптотику общего члена ряда при n , отбросив в числителе и знаменателе дроби меньшие степени n . Так как последовательность

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.03.20151.37 Mб46Метод пособие PowerPoint.doc
#
26.03.20151.76 Mб95Метод пособие Word.doc
#
01.05.2019193.54 Кб1метод рекомендации курсовой мат методы.doc
#
26.03.201536.46 Кб58Метод рекомендации по группам риска.docx
#
23.11.201934.64 Кб3Метод рекомендации по группам риска.docx
#
26.03.20152.75 Mб12Метод-ка ВМ для ст.зу.Ч.2 к.р. 3,4..pdf
#
26.03.201534 Кб3Метод. рекомендации к диплому 2(2).docx
#
17.12.201874.75 Кб4Метод.реком. к написанию реферата.doc
#
26.03.2015165.38 Кб7метод.указ по кр скот-во.doc
#
27.09.2019410.11 Кб5Метод_указ_по_дисц.doc
#
11.03.201636.86 Кб19Методика проведения утреннего сбора.doc