Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новгородский Государственный Университет им. Ярослава Мудрого

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метод-ка ВМ для ст.зу.Ч.2 к.р. 3,4

..pdf

Скачиваний:

Добавлен:

26.03.2015

Размер:

2.75 Mб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

								10
8.	а)	y /	1 y 2		;			б) y//	9 y e3x ,	y(0) y/ (0) 0.
				xy

9.	а)	y /	y	sin		y	;	б) y// 5y/	6y sin 3x ,	y(0) 1, y/ (0) 0 .
			x			x

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 3

Криволинейные интегралы

Задание 1. Криволинейный интеграл первого рода

Пусть гладкая кривая L в пространстве задана параметрически равенствами x x(t), y y(t), z z(t) , где параметр t меняется в пределах T1 ,

T2 , то есть T1 t T2 . Предположим, что на этой кривой распределена масса или электрический заряд с плотностью f (x, y, z) . Тогда масса всей кривой или величина суммарного заряда определяется следующим инте-

гралом f (x, y, z)dL , который называют криволинейным интегралом пер-

вого рода.

Вычисляется этот интеграл с помощью определѐнного интеграла по следующей формуле

f (x, y, z)dL =

f (x(t), y(t), z(t))

(x/ )2 ( y / )2

(z / )2 dt .

Основными свойствами криволинейного интеграла первого рода яв-

ляются линейность и аддитивность:

1) C f (x, y, z)dL C f (x, y, z)dL , ( f g)dL f dL + g dL ;

2) если кривая L состоит из двух частей L1

и L2 , тогда f (x, y, z)dL

= f (x, y, z)dL + f (x, y, z)dL .

Пример.

Найти массу кривой x a cost, y asin t, z at 2 ,

0 t 2 с плотностью

f (x, y, z) = z . Находим x/ asin t, y/

a cost,

z / 2at ,

(x/ )2 ( y/ )2

(z/ )2 =

(asin t)2 (a cost)2 (2at)2 =

4a2t 2 .

Следовательно,

масса

всей

рассматриваемой

кривой

z dL

1 4t 2 ,

1 16

at 2

a2 4a2t 2 dt = a

1 4t 2 dt =

2xdx 8tdt,

= a

14 x 2 dx

tdt

xdx

1 16 2

a a x

a a

(1 16 2 )3 1 .

Криволинейный интеграл второго рода

Пусть в каждой точке кривой L задан вектор (например, сила) F(x, y, z) P(x, y, z)i Q(x.y, z) j R(x, y, z)k . Тогда работа, совершаемая этой силой по перемещению материальной точки из точки A с координатами x(T1 ), y(T1 ), z(T1 ) в точку B с координатами x(T2 ), y(T2 ), z(T2 ) опреде-

ляется

интегралом

F d r =

P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz , где

d r dx i dy j dzk .

Этот интеграл называется криволинейным интегра-

лом

второго рода и

вычисляется по формуле

F d r =

[P(x(t), y(t), z(t))x/ (t) Q(x(t), y(t), z(t))y / (t) Q(x(t), y(t), z(t))z / (t)]dt .

Кроме свойств линейности и аддитивности криволинейный интеграл второго рода обладает следующим свойством: если точка движется по кривой в обратном направлении от точки B к точке A , тогда интеграл меняет знак. Если обозначить L движение вдоль кривой L в направлении возрастания параметра t от точки A к точке B , а L движение в обратном

направлении, то F d r = – F d r .

Пример. Вычислим работу силы F x2 i y2 j z2 k вдоль замкнуто-

го контура треугольника O(0,0,0),

A (1,1,1),

B (1,1,0), О(0,0,0). По свойству

аддитивности F d r =

F d r +

F d r . Составим параметри-

ческие уравнения прямых OA, AB, BO. Направляющий вектор прямой OA имеет координаты (1,1,1). Следовательно, еѐ каноническое уравнение име-

ет вид 1x 1y 1z , а параметрическое уравнение: x t, y t, z t, где пара-

метр t меняется от 0 до 1 при движении в направлении OA . Аналогично,

получим уравнение прямой AB: x 1, y 1, z t, где параметр t																											меняется от
1 до 0 при движении										в направлении										AB ,	и уравнение прямой BO :
x t, y t, z 0, где					параметр									t		меняется					от 1	до		0. Таким						обра-
		1									1								1				0				t	3	0		1
зом, F d r = (t			2		2			2			=				2			3	1		F d r = t				2		t		0		1
				t		t				)dt			3t			dt t			\|	1,						dt			\|			, а
				t		t				)dt			3t			dt t			\|	1,						dt	3		\|		3	, а
OA	0										0								0		AB	1					3		1		3
					0							2t	3	0			2
		F d r =					2		dt			2t		0			2
интеграл						2t								\|				.		Следовательно,					искомая					работа
интеграл						2t					3			\|			3	.		Следовательно,					искомая					работа
	BO				1						3			1			3

F d r =

						13
1	1		2	= 0.
1				= 0.
3			3
					Двойной интеграл
		Задание 2. Двойной интеграл
		Пусть функция f (x, y) непрерывна в ограниченной области (оме-
га) на плоскости XOY. Если в области распределена масса или элек-
трический заряд с плотностью						f (x, y) , тогда масса всей области или
суммарная величина					заряда	вычисляется	с	помощью	интеграла
f (x, y)dxdy , который					называется двойным		интегралом от функции

f (x, y) по области .
		Основными свойствами двойного интеграла являются: 1) линей-
ность:				C f (x, y)dxdy C f (x, y)dxdy ,			где	C –	постоянная,

( f g)dxdy =	f (x, y)dxdy g(x, y)dxdy 2) аддитивность: если область

1 2 (область состоит из двух частей, котрые могут пересекать-

ся по кривой), тогда f (x, y)dxdy =		f (x, y)dxdy f (x, y)dxdy .
	1	2
Вычисление двойного интеграла сводится к повторному интегриро-
ванию, то есть к двукратному вычислению определѐнного интеграла.

Пусть область является криволинейной трапецией относительно оси OX, то есть является частью плоскости, ограниченной прямыми x a ,

x b ( a b ) и кривыми	y (x), y (x) , где (x) (x) для всех значе-
ний x [a,b] . Тогда
	b	(x)
	f (x, y)dxdy =	f (x, y)dy dx .
		(x)
	a	(x)

Сначала вычисляется внутренний интеграл в предположении, что f (x, y) является функцией одной переменной y ( x считается постоянной),

а затем вычисляется интеграл от функции одной переменной x по промежутку [a,b] .

Пример. Вычислим (x y)2 dxdy , где область является частью

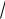плоскости, ограниченной кривыми y x2 , y x . Из равенства x2 x находим точки пересечения этих кривых x1 0, x2 1. Следовательно,

																						14

a 0,b 1. Так как											x x2				для всех x [0,1], то кривая																		y		x ограничива-
ет область интегрирования сверху, а кривая																										y x2			снизу. Таким образом,
																									1
										1					x
										1					x												3					x
имеем (x y)2 dxdy =														(x y)							2 dy dx =						(x y)				\|		dx	=
имеем (x y)2 dxdy =														(x y)							2 dy dx =						3				\|		dx	=
																											3			x		2
										0				x2											0					x
	1																		1
1	(x					)3 (x x				2 )3 dx						=		1		3x2					3x2 x				3x4 3x5 3x6 dx =
1	(x				x	)3 (x x				2 )3 dx						=		1		3x2			x		3x2 x			x	3x4 3x5 3x6 dx =
3	0																	3	0
	0																		0
1	6							2					3					1			3				1	1	6				2		3	1			3		51
1	6	3	x x				3	2	2			x	3			5		1		6	3			7	\| =	1	6				2		3	1			3		51
3	7 x		x x					5 x				x	5 x					2 x			7 x				\| =	3	7 1				5		5			2	7 = 70 .
																									0
		Если функция										f (x, y)					≡ 1, тогда							f (x, y)dxdy							=		dxdy					– площадь

области .
		Пример. Вычислим площадь фигуры, ограниченной линиями y x2 ,

																																		1				x
																											S = dxdy =										dy		dx =
y x (смотри предыдущий пример). Имеем,																											S = dxdy =										dy		dx =
																																		0			x2
																																		0			x2
	1																1
=		x x2 dx = 2 x x 1 x3																\| = 1.
	0							3					3				0
	0																0
		Если область не является криволинейной трапецией относительно
оси OX,				тогда разбивается прямыми, параллельными оси OY, на части

1 , 2 , , каждая из которых является криволинейной трапецией относительно оси OX. После этого вычисляют двойной интеграл, используя свой-

ство аддитивности f (x, y)dxdy =			f (x, y)dxdy f (x, y)dxdy .
		1	2
Пример. Вычислим	(2x y)2 dxdy , если область			ограничена ли-

ниями x=0, y=x, y=x+1, y=2. Эта область не является криволинейной трапецией относительно оси OX, но прямая x=1 разбивает эту область на две части 1 ={(x,y): 0 x 1, x y x 1}, 2 ={(x,y): 1 x 2, x y 2 }, каждая из которых является криволинейной трапецией. По свойству аддитивности

двойного интеграла имеем (2x y)2 dxdy =												(2x y)2 dxdy					+ (2x y)2 dxdy
												1							2
1	x 1			2	2				1	1				x 1		2		1			2
= dx (2x y)		2	dy +	dx (2x y)		2		=		1		y)	3	\|		+		1	(2x y)	3	\|		=
							dy				(2x				dx							dx
							dy			3	(2x				dx			3				dx
0	x			1	x				0					x		1					x

	1	1	(2x x 1)3 (2x x)										3 dx					1	2	(2x 2)3 (2x x)3 dx =												1	1	(3x 1)3 27x3 dx +
	1															+		1														1
3																+	3														3
3		0															3		1												3		0
		0																	1														0
		2													1												2
	1		(2x 2)3 27x3 dx =											1		27x 2 9x 1 dx							+		1		8 12x 24x2 19x3 dx =
3			(2x 2)3 27x3 dx =										3			27x 2 9x 1 dx							+	3			8 12x 24x2 19x3 dx =
3		1											3		0									3		1
		1													0											1
	1			3		9		2		1		1			3		2				19		4	2				29		28	23			101
		9x					x		x	\|	+		8x			6x				8x		x		\| =											.
		9x					x		x	\|	+		8x			6x				8x		x		\| =											.
	3					2				0		3									4			1				6		3	4			12
										0														1
					Пусть область интегрирования является криволинейной трапеци-
ей относительно оси OY, то есть является частью плоскости, ограниченной
прямыми y=c, y=d (c < d) и кривыми x ( y), x ( y) ,																																		где ( y) ( y) для
всех значений										y [c, d ] .						Тогда двойной интеграл вычисляется повторным
интегрированием следующим образом
																								d ( y)
															f (x, y)dxdy								=					f (x, y)dx
															f (x, y)dxdy								=					f (x, y)dx			dy .
																								c			( y)
																								c			( y)
					Сначала вычисляется внутренний интеграл в предположении, что
	f (x, y) является функцией одной переменной																												x (y считается постоянной),

а затем вычисляется интеграл от функции одной переменной y по промежутку [c, d ] .

Пример. Вычислим	dxdy		, если область	ограничена линиями
		2
(x y)

y = 1, y=x, y=x+1, y=2. Эта область не является криволинейной трапецией относительно оси OX, но является трапецией относительно оси OY. следо-

					dxdy						2		y		dx					2		1	y				2		1	1
					dxdy			2							dx			2				1	\|	dy =					1	1
								2										2					\|
вательно,										=		dy							=												dy	=
					(x y)						1	y 1			(x y)					1		x y y 1					1		2 y	2 y 1

	1	ln			1	ln			2	=	1			2 y 1			2		1	ln		ln1		=	1	ln		.
		ln				ln			\|	=		ln					\| =			ln		ln1		=		ln		.
			(2 y	1)			y														3						3
			(2 y	1)			y														3						3
2					2			\|1			2				y	1			2		2				2		2
2					2			\|1			2				y	1			2						2

Переход к полярным координатам в двойном интеграле

Пусть точка M в декартовой системе имеет координаты x,y. Тогда полярным радиусом этой точки называют расстояние от точки M до начала координат или длину радиус – вектора OM этой точки, а полярным углом называют угол, который радиус – вектор OM образует с осью OX. Полярный радиус обозначают r, а полярный угол . Связь декартовых координат

точки с полярными осуществляется равенствами

x r cos , y r sin .

Если область интегрирования является кольцевым сектором, то есть в декартовых координатах задаѐтся системой неравенств

		2	x	2	y	2	R		2	,
R			x		y		R			,
	1							2
		k x y k					2	x,
			1				2

тогда в полярной системе координат эта область будет являться прямоугольником R1 r R2 , 1 2 , где полярные углы 1,2 определяются

из равенств tg 1 k1,tg 2 k2.

Переход в двойном интеграле от декартовых координат к полярным координатам осуществляется по формуле

f (x, y)dxdy		f (r cos , r sin )rd dr ,
	/

которая, в случае, когда область интегрирования является кольцевым сектором, принимает следующий вид

f (x, y)dxdy

d f (r cos, r sin ) r dr.

(1)

Пример. Вычислим двойной интеграл 1 x2

y2 dxdy , если об-

ласть интегрирования задана неравенствами

1 x2

x y

3 x.

В этом случае имеем R1 1, R2

2 ,

а tg 1 1,tg 2

Следова-

тельно,

, и рассматриваемый интеграл, согласно формуле (1),

будет равен 1 x2

y2 dxdy =

1 r 2

r dr = (так как внутренний

интеграл не зависит от ) =

1 r 2

r dr

= (после замены перемен-

ной t

1 r 2

, t 2

1 r 2 , 2tdt 2rdr или tdt rdr ) =

t 2dt

12 3

5 5 2 2

= (5 5 2 2) .

Тройной интеграл

Если в области V трѐхмерного пространства распределена масса или

электрический заряд с плотностью

f (x, y, z) , тогда масса этой области или

суммарный электрический заряд определяются с помощью тройного инте-

грала f (x, y, z)dxdydz , который обладает теми же свойствами, что и

двойной интеграл (линейность, аддитивность и т.д.).

Вычисление тройного интеграла, также как и двойного, производится с помощью повторного интегрирования. Пусть область V является ци-

линдрической	относительно	оси OZ: ограничена снизу		поверхностью
S1 : z (x, y) (нижнее основание), ограничена сверху поверхностью
S2 : z (x, y)	(верхнее основание), (x, y) (x, y) , а образующая парал-
лельна оси OZ. Тогда справедливо равенство
		( x, y)
	f (x, y, z)dxdydz dxdy		f (x, y, z)dz,	(2)
	V	Vxy	( x, y)

где Vxy – проекция цилиндра V на плоскость XOY.

dxdydz

Пример. Вычислим тройной интеграл , если область

V 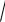1 x y z

интегрирования V является тетраэдром, который ограничен плоскостями x 0, y 0, z 0, x y z 3.

Очевидно, область V является цилиндрической относительно оси OZ,

которая ограничена снизу плоскостью				z 0 , ограничена сверху плоско-
стью z 3 x y , а проекцией Vxy			тетраэдра на плоскость XOY является
треугольник, ограниченный прямыми				x 0,	y 0, x y 3.			Согласно
		dxdydz			3 x y		dz
формуле (2) имеем		dxdydz	=	dxdy			dz	= (пере-


	1	x y z				1 x y z
V	1	x y z		Vxy	0	1 x y z
V				Vxy

ходим к повторному интегрированию в полученном двойном интеграле) =

3	3 x		3 x y					dz
dx		dy						dz				= (вычисляем					внутренний				интеграл)				=


							1 x y z
0	0		0				1 x y z
3	3 x								3 x y			3	3 x
3	3 x	2							\|			3	3 x
dx		2		1 x y z					\|	dy		= dx		4 2		1 x y			dy = (вычислим внут-
0	0							0				0	0
						3				4			3		3 x	3				32		4		3
ренний интеграл)								4 y			(1	x y)2			\| dx =		4(3	x)					(1	x)2	dx
ренний интеграл)								4 y		3	(1	x y)2			\| dx =		4(3	x)		3		3	(1	x)2	dx
= 4		(3 x)				0				3					0	0				3		3
= 4		(3 x)			2		32 x 4			2 (1 x) 2			\| = 8 16 2 32 8 18 38 .
					2							5	3
			2			3		3		5			0	15				15				15

Тройной интеграл используется для вычисления объѐма пространст-

венных тел, который равен dxdydz .

Пример. Вычислим объѐм части цилиндра x2 y2 a2 , заключѐнной между плоскостями x y 2z 2a , x y z 2a .

По

условию,

данное

тело V ограничено

снизу

плоскостью

z a

, а сверху плоскостью z 2a x y . Проекцией этого тела на

координатную плоскость XOY является круг x2 y2

a2 . Следовательно,

dxdydz

2a x y

искомый

объѐм

равен

dxdy

Vxy

a 2

2a x y a

dxdy

Vxy

полярным

координатам)

ar 1 r 2

cos 1 r 2 sin dr

1 a3

cos 1 a3 sin d

											x			y
							a									dxdy		= (перейдѐм к
							a									dxdy		= (перейдѐм к
x	2	y	2	a		2					2			2
x		y		a
		2					a	a			1 r cos 1 r sin rdr
		d						a			1 r cos 1 r sin rdr													=
		0					0				2					2
		0					0
		2					1			2			1		3			1	3	sin	a
=					2 ar								6 r			cos 6 r				sin	\|	d
			0																		0
		1							1							1				2
		1			3				1		3					1	3	cos \| =			a		3
= 2 a									6 a			sin 6 a						cos \| =			a			.
																				0

Поверхностные интегралы

Задание 3. Поверхностный интеграл первого рода.

Пусть в каждой точке поверхности S определена функция f (x, y, z) ,

которая может являться плотностью массы или электрического заряда распределѐнного по этой поверхности. Тогда масса всей поверхности или суммарный заряд определяются при помощи поверхностного интеграла первого рода

f (x, y, z) dS .

Основными свойствами этого интеграла являются свойства: 1) ли-

нейность, то есть ( f	g) dS	= f (x, y, z) dS + g(x, y, z) dS , где
S		S	S
, – постоянные; 2) аддитивность, то есть			f (x, y, z) dS = f (x, y, z) dS
		S	S1
+ f (x, y, z) dS , где S1 ,	S2 – части поверхности S, которые могут пересе-
S2
каться только по линии и S1 S2		S ; 3) если	f (x, y, z) 1, тогда dS –

площадь поверхности S.

Вычисление поверхностного интеграла первого рода

Пусть поверхность S задана в декартовых координатах уравнением z (x, y) (либо y (x, z) или x ( y, z) ), тогда эта поверхность одно-

значно проектируется на координатную плоскость XOY (на координатные плоскости XOZ или YOZ ) и эту проекцию будем обозначать S xy . Тогда

поверхностный интеграл первого рода вычисляется по такой формуле

f (x, y, z) dS

f (x, y, (x, y))

dxdy.

Sxy

Пример. Вычислить

(x2 y2

z)2 dS , где поверхность S является

частью параболоида z x2

y2 ,

z 2 .

данном

случае (x, y) x2

y2 ,

2x,

2 y , проекцией

части параболоида на плоскость

XOY является круг x2 y2 2 . Сле-

довательно, (x2 y2 z)2 dS = (x2 y2

x2 y2 )2

1 4x2 4 y2 dxdy

Sxy

= (перейдѐм к полярным координатам в последнем интеграле) =

r r 4

1 4r 2 dr

1 4r 2 dr = (произведѐм замену пе –

= 4

= 8

, t 2 1 4r 2 , 2tdt 8rdr, rdr 1 tdt, r 2 t2 1) = 8

ременной

1 4r 2

t 1 tdt

= t 6 2t 4 t 2 dt = t7

2 t5

t3 | =

109 .

8 0

315

Если поверхность S проектируется на координатную плоскость не однозначно, тогда еѐ разбивают на не пересекающие части, каждая из которых однозначно проектируется на координатную плоскость, а затем пользуются свойством аддитивности.

Пример. Вычислить

x2 dS , где S –

полная поверхность сферы

x2 y2 z2 a2 .

Сфера неоднозначно проектируется на плоскость XOY , поэтому ра-

зобьѐм еѐ на две полусферы S

, уравнение которой z

a2 x2

y2 ,

, уравнение которой

a2 x2

y2 .

Проекцией полусфер S

на

координатную

плоскость

XOY

является круг K : x2 y2

a2 ,

для обеих полусфер

и S

a2 x2 y2

a2 x2

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.03.20151.37 Mб46Метод пособие PowerPoint.doc
#
26.03.20151.76 Mб95Метод пособие Word.doc
#
01.05.2019193.54 Кб1метод рекомендации курсовой мат методы.doc
#
26.03.201536.46 Кб58Метод рекомендации по группам риска.docx
#
23.11.201934.64 Кб3Метод рекомендации по группам риска.docx
#
26.03.20152.75 Mб12Метод-ка ВМ для ст.зу.Ч.2 к.р. 3,4..pdf
#
26.03.201534 Кб3Метод. рекомендации к диплому 2(2).docx
#
17.12.201874.75 Кб4Метод.реком. к написанию реферата.doc
#
26.03.2015165.38 Кб7метод.указ по кр скот-во.doc
#
27.09.2019410.11 Кб5Метод_указ_по_дисц.doc
#
11.03.201636.86 Кб19Методика проведения утреннего сбора.doc