1. Вопрос 1. Понятия вычислительного приема и вычислительного навыка..Классификация вычислительных приемов

Вычислительный прием - это способ нахождения результата арифметического действия.

Вычислительный навык - это вычислительный прием, доведенный до автоматизма или высокая степень овладения вычислительным приемом.

Приобрести вычислительный навык - это значит для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результаты арифметических действий.

Все вычислительные приемы делятся на две группы: устные и письменные.

Устные и письменные приемы имеют сходство и различия. Покажем основные отличия в таблице.

Устные вычислительные приемы	Письменные вычислительные приемы
1. Выполняются устно, записываются в строчку: 34+20=(30+4)+20=(30+20)+4=54	1. Выполняются в столбик: 25 +18 43
2. Операции начинают выполня­ться с единиц высших разрядов	2. Операции начинают выполнять с единиц низших разрядов
3. Промежуточные результаты запоминаются, записываются только на стадии ознакомления	3. Промежуточные результаты записываются
4. Теоретическая основа может быть различна: 12+12+12+12+12=60. Т.о. - конкретный смысл арифметического действия умножения. 125=(10+2)5=105+25=60. Т.о. - свойство умножения суммы на число. 125=1210:2=60. Т.о. - изменение результата в зависимости от изменения одного из компонентов.	Теоретическая основа всегда единственна. Приемы основаны на принципе по разрядности
5. Рассматриваются на области чисел, начиная с 10 и до многозначных чисел, где вычисления не затруднены	Рассматриваются на области чисел, начиная с сотни и до бесконечности.

Устные и письменные вычислительные приемы имеют сходство. Все вычислительные приемы основаны на знании теоретического материала. В зависимости от теоретического материала они делятся на шесть групп.

I группа. Вычислительные приемы, основанные на знании нумерации:

1. Знание принципа образования натуральной последовательности. Слу­чаи вида: а+1.

Дети должны усвоить, что для того чтобы прибавить 1, надо назвать следующее число; вычесть 1 - назвать предыдущее число: 7+1; 26-1; 393+1; 10000-1.

2. Знание разрядного состава чисел. Случаи вида:

40+5 100+40+7

45-5 147-100

45-40 147-40

147-7

40+5=45 - рассуждения учащихся могут быть такие: 4 десятка и 5 единиц образуют число 45.

45-5=40 - если из 4 десятков и 5 единиц вычесть 5 единиц, то получим 4 десятка.

45-40=5 - если из 4 десятков и 5 единиц вычесть 4 десятка то получим 5 единиц.

3. Прием, основанный на знании поместного значения цифры (позиционного принципа записи чисел). В зависимости от того, на каком месте (позиции) стоит цифра в записи числа , она имеет разное значение. В эту группу входят случаи умножения и деления на 10, 100, 1000 без остатка.

Умножить на 10, значит приписать один нуль (7 умножить на 10, 7 записываем на второе место справа, на место десятков). Разделить на 10, значит отбросить один нуль.

Примеры:

710 70:10

7100 700:100

71000 7000:1000.

II группа. Вычислительные приемы, теоретической основой которых является знание конкретного смысла арифметических действий.

1. Случаи вида: а+2, 3, 4, 0, (5+5), (в пределах 20). Применяется прием присчитывания и отсчитывания по одному и группами:

3+2=5 (объединяем 3 да 2) 5-2=3

3+1=4 5-1=4

4+1=5 4-1=3

2. Случаи вида: 9+5=14 12-5=7.

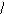
9+1+4 12-2-3

3. Случаи сложения и вычитания разрядных чисел:

40+30=70 - 4 десятка плюс 3 десятка равно 7 десятков.

40-30=10 - 4 десятка минус 3 десятка получим 1 десяток.

800-400=400 - 8 сотен минус 4 сотни получим 4 сотни.

5000+3000=8000 - 5 тысяч плюс 3 тысячи получим 8 тысяч.

Случаи сложения и вычитания сводятся к сложению и вычитанию однозначных чисел.

Теоретическая основа - конкретный смысл сложения и вычитания.

4. Случаи табличного умножения, когда первый множитель меньше или равен второму.

Например: 23; 28; 35; 44.

Теоретическая основа - конкретный смысл умножения.

5. Случаи вне табличного деления, теоретической основой которых является конкретный смысл деления с остатком; конкретный смысл деления.

29:7=4 (остаток 1); 86:10=8 (остаток 6); 90:3=30.

6. Случаи умножения 0 и 1 на число, теоретической основой которых является конкретный смысл умножения.

1а=а 15=1+1+1+1+1=5 (по 1 взяли 5 раз)

0а=0 05=0+0+0+0+0=0

III группа. Вычислительные приемы, теоретической основой которых является знание правил. Сюда входят случаи умножения любого числа на 0 и 1, невозможность деления на 0.

а0; а1; а:0 (делить нельзя);

70=0 250=0;

71=7 251=25.

IV группа. Вычислительные приемы, теоретической основой которых является знание взаимосвязи между результатами и компонентами арифметических действий.

1. Случаи вида: а-5, 6, 7, 8, 9 (в пределах 10). 8-6=2 8=6+2 8-6=2

Рассуждение учащихся: какое число надо прибавить к 6, чтобы получить 8, 8 - это 6 и 2, значит, если из 8 вычесть 6, получится 2.

2. Случаи вычитания в пределах 20 вида: 12-5=7

Теоретической основой случаев 1, 2 является взаимосвязь между результатами и компонентами действия сложения.

3. Все случаи табличного деления:

21:7=3 54:6=9

4. Случаи деления разрядного числа на разрядное вида:

90:30=3, т.к. 303=90

800:400=2, т.к. 4002=800

5. Случаи внетабличного деления неразрядного числа на неразрядное вида:

54:18=3, т.к. 183=54

6. Случаи деления 0 на число и числа на 1

а:1=а 0:а=0

Например: 0:2=0, т.к. 02=0

3:1=3, т.к. 31=3

Теоретической основой случаев 3, 4, 5, 6 является взаимосвязь между результатами и компонентами действия умножения.

V группа. Вычислительные приемы, теоретической основой которых является изменение результатов в зависимости от изменения одного из компонентов (сюда входят приемы рациональных вычислений):

1. Приемы округления: 399+566=965 966-1=965 400+566=966

Здесь удобно первое слагаемое округлить до 400. Найдем сумму, чтобы сумма не изменялась, из результата вычтем 1.

2. Случаи умножения и деления на 5, 25, 50.

Примеры вида: 1850=900

Рассуждения: 50=100:2, значит 18100=1800, т.к. второй множитель увеличили в 2 раза, чтобы произведение не изменилось, его нужно разделить на 2.

Рассуждения: если первый множитель четное число и в данном случае делится на 2 рассуждать можно следующим образом: 1850=18:2100=900

Пример вида: 1625=400.

1625=400; 25=100:4, значит 16100=1600 1600:4=400.

Рассуждения: если второй множитель увеличили в 4 раза, значит, чтобы произведение не изменилось, его нужно уменьшить в 4 раза. Или: 16:4100=4100=400

Рассуждения: первый множитель уменьшаем в 4 раза, чтобы произведение не изменилось, его нужно увеличить в 4 раза.

Пример деления вида:

400:25=16 400:100=4 44=16.

Рассуждения: т.к. делитель увеличили в 4 раза, частное в 4 раза уменьшилось, следовательно, чтобы результат не изменился, частное нужно увеличить в 4 раза.