2.5. Закон Архимеда

Пусть в жидкость погружен параллелепипед объемом W(рис. 2.13).

Рис. 2.13

На него действуют следующие силы: сверху сила давления от столба жидкости , снизу –, гдеS– площади нижней и верхней граней параллелепипеда; равнодействующая сил давлений, действующих на боковые грани, равна нулю, так как они равны и противоположно направлены. Спроектируем силы на вертикальную ось, вес тела учитывать не будем. Отметим, что согласно закону Паскаля давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково, поэтому давление на внешней поверхности действует по всем граням одинаково и во взаимно противоположных направлениях, поэтому результирующая сила равна нулю.

, откуда

;.

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной этим телом.

В случае тела произвольной формы, погруженного в жидкость, закон Архимеда выводится, привлекая дополнительные рассуждения.

2.7. Равномерное вращение сосуда с жидкостью

Вращение сосуда с жидкостью вокруг вертикальной оси

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная по­верхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.15).

Рис. 2.15

На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны gи. Равнодействующая массовая силаjувеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.

Учитывая, что сила нормальна к свободной поверхности, получим , отсюда или после интегрирования .

В точке пересечения свободной поверхности с осью вращения C=h иr=0, поэтому окончательно будем иметь

, (2.10)

где .

Таким образом, свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить, используя выражение (2.10) и исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.

Запишем закон изменения давления во вращающейся жидкости в функции радиуса и глубины относительно верхней точки жидкости (без вывода):

.

Вращение сосуда с жидкостью вокруг горизонтальной оси

При таком вращении угловая скорость столь велика, что(действие силы тяжести можно не учитывать). Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементар­ного объема с площадью основанияdSи высотойdr, взятой вдоль радиуса (рис. 2.16). На выделенный элемент жидкости действуют силы давле­ния и центробежная сила.

Рис. 2.16

Обозначив давление в центре площадки dS, расположенной на радиусеr, черезp, а в центре другого основания объема (на радиусеr+dr) черезp+dp(разложилиpв ряд Тейлора, но так как в данном случаеpзависит только отr, тоdr/drсократился), получим следующее уравнение равновесия выделенного объема в направлении радиуса

или .

После интегрирования получим . ПостояннуюCнайдем из условия, что приr=r₀p=p₀, следовательно, .

Подставив ее значение в предыдущее уравнение, получим связь между pиrв следующем виде:

. (2.11)

Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом rи ширинойdr. Используя формулу (2.11), получим

,

а затем следует выполнить интегрирование в требуемых пределах:

.

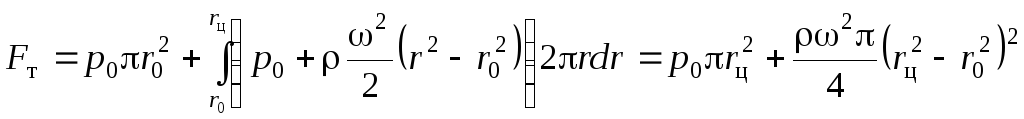Если равно внешнему давлению, то .

При большой скорости вращения жидкости получается значительная суммарная сила давления F_бна боковую стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.

Приведем выражение для определения силы F_ббез вывода:

, где– длина цилиндра.