Mashkovsky_Lesnaya_biometria

приведено распределение деревьев по диаметру на высоте груди. Половина объема данной выборки составит

n2 = 2182 =109.

Первым интервалом, чья накопленная частота превышает это значение (медианным интервалом), будет интервал 21,95–24,65. Подставляя необходимые значения в формулу (91), получим

= 22,0 + 2,7 3240 = 24,16.

Квантили. Медиана делит вариационный ряд на две равные части. В более общем случае мы можем разделить вариационный ряд на две неравные части в любом соотношении. Статистики, которые отделяют от вариационного ряда определенную часть его членов, называются квантилями.

Квантили, которые отделяют от вариационного ряда 1, 2, ..., 99 % его членов, называются перцентилями. С помощью 99 перцентилей P1, P2 , ..., P99 вариационный ряд делится на 100 равных

частей. Девять статистик, которые делят вариационный ряд на десять одинаковых частей, называются децилями. Квартилями называют три квантиля (Q1 , Q2 и Q3 ), которые делят вариационный ряд на четыре

равные части. Они соответствуют перцентилям, отделяющим от ранжированного ряда наблюдений 25, 50 и 75% вариант соответственно:

Q1 = P25 ;

Q1 = P50 ;

Q1 = P75.

Кроме того, квартиль и перцентиль, делящие вариационный ряд на две равные части, соответствуют медиане ряда наблюдений:

Q2 = P50 = Me.

На практике чаще всего используют перцентили P3 , P10 , P25 , P50 , P75 , P90 и P97 . Определяют квантили аналогично тому, как определяют медиану вариационного ряда. В том случае, если

82

где PL – квантиль, отделяющий от ранжированного ряда L процентов наблюдений; xнL – нижняя граница интервала, в который попадает квантиль PL ; j – номер интервала, в который попадает квантиль PL ; L

– процент наблюдений в выборке, которые меньше, чем квантиль PL ;

j−1

∑ fi – накопленная частота интервала, предшествующего интервалу,

i=1

в котором находится квантиль PL . Для того чтобы определить, в каком

интервале находится квантиль, следует воспользоваться накопленными частотами ряда распределения. Первый интервал, у которого накопленная частота окажется больше, чем величина L n100 , и будет таким классом.

В качестве примера найдем квартили распределения деревьев по диаметру на высоте груди (табл. 11). Квартиль Q1 попадает в интервал

19,25–21,95, так как это первый интервал, чья накопленная частота (77) оказалась больше величины:

100L n = 25100218 =54,5.

Подставляя необходимые значения в формулу (92), получим

Аналогичным образом определяем значения остальных двух квартилей распределения:

83

и

84

3. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

Лесная биометрия имеет дело с признаками, характеризующими различным образом лес в целом или отдельные его элементы. Для природных объектов свойственна изменчивость, т. е. признаки, которые их характеризуют, изменяются от объекта к объекту. Значение таких признаков определяется влиянием на объект множества различных, как правило, неизвестных случайных причин. В связи с этим признаки, характеризующие природные объекты, сами являются случайными величинами.

3.1.Функция распределения

Любая случайная величина подчинена какому-либо закону распределения, который может быть описан с помощью функции, определяемой соотношением

FX (x) = P( X < x)

и называемой функцией распределения величины X. Функция распределения обладает рядом свойств.

7. Функция распределения может принимать значения в интервале от 0 до 1 включительно:

0≤ F(x) ≤1.

8.Функция распределения является неубывающей функцией, т. е. для любых x1 и x2 таких, что x1 ≤ x2 , справедливо неравенство

F (x1) ≤ F (x2 ),

так как вероятность того, что случайная величина попадет на отрезок ] −∞; x2[ не меньше, чем вероятность попадания этой случайной

величины на отрезок ] −∞; x1[ , если x2 ≥ x1 .

9.При x, стремящемся к −∞, функция распределения стремится к нулю:

lim F(x) = 0,

x→−∞

а при x, стремящемся к +∞, функция распределения стремится к единице:

lim F (x) =1.

x→+∞

85

Кроме того, следует заметить, что величина F(b) − F(a)

представляет собой вероятность того, что случайная величина X примет значение, принадлежащее интервалу a ≤ X < b . Если верхняя граница b такого интервала равна +∞, то событие, состоящее в том, что случайная величина попадает в интервал [a; +∞[ есть не что иное,

как событие, состоящее в том, что случайная величина окажется больше или равной величине a. Вероятность такого события равна

P(X ≥ x) = F(+∞) − F(x),

или с учетом свойства 3 функции распределения

P(X ≥ x) =1− F(x).

3.2.Дискретные случайные величины

Случайные величины могут быть дискретными или непрерывными.

Дискретными называются случайные величины, принимающие конечное или счетное множество2 значений. В качестве примера возьмем число порослевин от основания усохших после пожара берез или число яиц в кладках соснового пилильщика и т. д.

Известно много законов распределения дискретных случайных величин. В качестве примера рассмотрим биномиальное распределение.

3.2.1.Биномиальное распределение

Представим себе такую ситуацию: создаются лесные культуры дуба черешчатого строчно-луночным посевом желудей. Желуди высеваются в лунки, расположенные строчками через 0,7 м с расстоянием между строчками 1,2 м. В каждую лунку кладется по пять желудей. Часть из них взойдет, а другая часть не даст всходов. Предположим, что для высеваемой партии желудей была определена всхожесть семян. Всхожесть – это отношение числа семян, которые дали всходы, к общему количеству высеяных семян, выраженное в процентах. Обозначим символом p всхожесть, деленную на 100, т. е. p

– это отношение числа семян, которые дали всходы, к общему количеству высеяных семян или, другими словами, p – это

2 Множество называется счетным, если можно установить взаимно однозначное

соответствие между ним и множеством натуральных чисел.

86

вероятность того, что желудь взойдет. Попробуем определить вероятность того, что в лунке взойдет 5 желудей, 4, 3, 2, 1 или не взойдет ни одного. Для удобства пронумеруем все желуди, высаженные в лунку, номерами с 1-го по 5-й. Теперь рассмотрим, какие могут быть варианты прорастания семян в лунке (табл. 25). Как видим, вероятность того, что в лунке не прорастет ни одного желудя,

составляет q5 , где q =1− p – вероятность того, что желудь не

прорастет. Может произойти 5 различных событий, в результате которых в лунке будет только один всход. Эти события состоят в том, что в лунке прорастет 1, 2, 3, 4 или 5-й желудь, а остальные не взойдут. Вероятность каждого из этих событий, согласно правилу

умножения вероятностей, равна p q4 . Таким образом, лунка, где есть только один росток, может встретиться с вероятностью 5 p q4 . Аналогичным образом, пользуясь данными табл. 25, получаем, что вероятность встретить лунку с двумя всходами будет равна 10 p2 q3 , с тремя всходами – 10 p3 q2 , с четырьмя – 5 p4 q и с пятью – p5

Таблица. 25. Возможные варианты прорастания желудей в лунке

87

Число событий, в которых имеется 0, 1, 2, 3, 4 или 5 взошедших желудей, есть не что иное, как биномиальные коэффициенты (число сочетаний из 5 по 0, 1, 2, 3, 4 или 5):

Учитывая последнюю формулу, вероятность того, что в лунке окажется m всходов, будет равна

88

C5m pm q5−m .

Если бы в каждую лунку высевали не 5, а n желудей, то вероятность того, что в лунке окажется m всходов, составила бы величину

Это выражение называется формулой Бернулли. В общем случае рассматриваемую выше ситуацию можно представить как n-кратное повторение эксперимента. Причем в результате каждого случайного эксперимента событие A может произойти с вероятностью p или не произойти с вероятностью q =1− p . Таким образом, мы получаем

случайную величину, представляющую собой число появлений события A в описываемой серии, состоящей из n независимых экспериментов. Эта случайная величина может принимать значения 0, 1, ..., n. Распределение, которому подчинена данная случайная величина, называется биномиальным, а вероятность того, что эта случайная величина будет равна m, определяется выражением (93).

3.3.Непрерывные случайные величины

Непрерывными называются случайные величины, которые могут принимать любые значения в каком-либо конечном или бесконечном интервале. Непрерывными случайными величинами являются такие параметры, как высота дерева, объем ствола и т. д.

3.3.1.Плотность распределения вероятностей

Плотностью распределения вероятностей P(x) непрерывной случайной величины X называется предел, если он существует, отношения вероятности попадания случайной величины X на интервал ]x, x + x[, примыкающий к точке x, к длине этого интервала, когда последняя стремится к нулю:

Кривая, изображающая плотность распределения вероятностей (плотность вероятности) непрерывной случайной величины,

называется кривой распределения.

Плотность вероятности обладает следующими свойствами.P(x) ≥ 0 для любого x, принадлежащего интервалу ]–∞;+∞[.

89

+∞

11. ∫P(x)dx =1, так как вероятность того, что непрерывная

−∞

случайная величина принимает значения из интервала ]–∞;+∞[, т.е. вероятность достоверного события равна единице.

12.P(x) – непрерывна или кусочно-непрерывна.

3.4.Нормальное распределение

Вкачестве примера для непрерывной случайной величины рассмотрим нормальное распределение. Это распределение имеет важное значение в биометрии. На практике очень часто изучаемые случайные величины следуют этому закону.Функция плотности вероятностей нормально распределенной случайной величины X имеет вид

−( x−m)2

=1 e 2 σ2 ,

σ 2 π

где m – математическое ожидание, а σ – среднее квадратическое отклонение случайной величины X. Эта функция называется кривой Гаусса. Она симметрична относительно прямой x = m и имеет колоколообразную форму.

При изменении величины m кривая будет смещаться влево или вправо, не меняя своей формы. Параметр m характеризует положение кривой на оси абсцисс, в связи с этим его иногда называют

параметром сдвига.

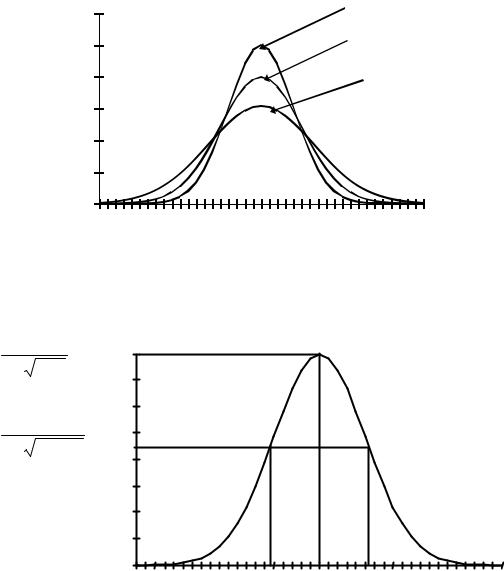
Стандартное отклонение σ определяет форму кривой Гаусса. При малых значениях этого параметра кривая имеет узкую и высокую вершину, а при больших значениях выглядит плосковершинной (рис. 12). Этот параметр иногда называют параметром масштаба.

Кривая Гаусса имеет максимум (т. max) в точке x = m , равный

и две точки перегиба (т. перегиба) с абсциссами m − σ и m + σ и ординатой

(рис. 13).

90

Площадь, ограниченная кривой Гаусса (как, впрочем, и любой другой кривой плотности распределения вероятностей) и осью абсцисс, равна 1. Причем основная площадь сосредоточена вблизи абсциссы, равной m. Так, например, площадь фигуры, ограниченной сверху кривой Гаусса, снизу – осью абсцисс, слева – вертикальной прямой, пересекающей ось абсцисс в точке m – σ, а справа – вертикальной прямой, пересекающей ось абсцисс в точке m + σ, равна 0,6827 (больше половины всей площади под кривой). Если слева и справа фигуру ограничить вертикальными прямыми, пересекающими

91