Mashkovsky_Lesnaya_biometria

32

Определим значения эмпирической функции распределения Fn (x) на основании данных интервальных вариационных рядов по

диаметрам и высотам деревьев в сосновом древостое (табл. 12 и 13). Для выполнения вычислений нам понадобятся накопленные частоты рядов распределения, которые, согласно (16), необходимо разделить на число наблюдений в выборке. Результаты вычисления значений эмпирической функции распределения приведены в табл. 15.

1.6.Графическое изображение статистических рядов

Графическое изображение вариационных рядов позволяет увидеть и проанализировать особенности варьирования изучаемого признака. Для этой цели используются различные типы графиков. При анализе массовых наблюдений для наглядного представления плотности распределения изучаемой случайной величины чаще всего применяются гистограмма и полигон распределения. Увидеть эмпирическую функцию распределения позволяет кумулята. Кроме кумуляты, для графического представления вариационных рядов используется огива. Для изображения таблиц распределения (корреляционных решеток) используют трехмерные графики, называемые призмограммами. Рассмотрим эти виды графиков.

Таблица 15. Эмпирические функции распределения диаметров и высот

деревьев в сосновом древостое

33

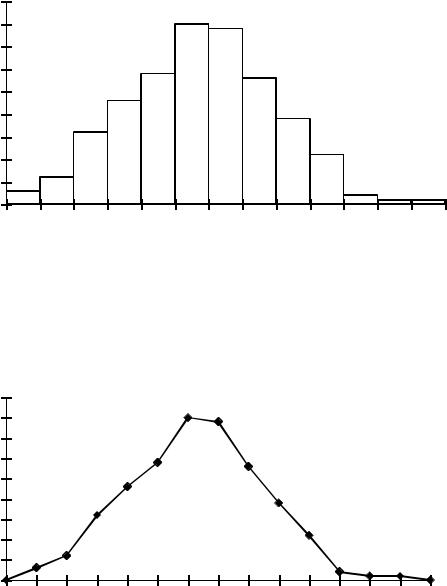
Гистограмма. Гистограммы распределения строятся только для интервальных вариационных рядов. При этом на оси абсцисс откладывают границы интервалов. График изображается в виде прямоугольников, основаниями которых служат интервалы ряда. Высоты прямоугольников должны соответствовать частотам (или частостям), откладываемым по оси ординат. На рис. 2 приведен пример гистограммы распределения диаметров в сосновом древостое, построенный по данным вариационного ряда, приведенного в табл. 11.

Полигон. Полигон распределения может строиться как для интервальных вариационных рядов, так и для дискретных. При его построении на горизонтальной оси откладывают значения классов, а по вертикальной – частоты или частости (рис. 3). Затем полученные точки соединяют прямыми линиями. При построении полигона используют два дополнительных примыкающих к вариационному ряду интервала, имеющих нулевые частоты. На рис. 3 изображен полигон, построенный для распределения деревьев в древостое по диаметрам для вариационного ряда, приведенного в табл. 11.

33

2. ОСНОВНЫЕ ПОКАЗАТЕЛИ ВЫБОРОЧНОЙ СОВОКУПНОСТИ

Группировка исходных данных и представление их в виде вариационных рядов позволяет представить статистические данные в компактном и обозримом виде. Представление статистических рядов в графическом виде дает информацию о характере распределения изучаемой случайной величины. Однако наряду с качественной характеристикой статистических данных часто необходимы количественные показатели, обобщающие информацию, содержащуюся в исходных данных.

Такие показатели можно разделить на несколько групп в зависимости от того, каким образом они характеризуют экспериментальные данные.

Первая группа показателей указывает на местоположение значений изучаемого признака на числовой оси. Они определяют ту величину, вокруг которой сосредоточены все значения изучаемого признака. К этой группе показателей относятся всевозможные средние величины.

Вторая группа характеристик выборки показывает, каким образом значения анализируемого признака располагаются вокруг средних значений. Эти показатели характеризуют степень изменчивости исходных данных. Они называются показателями вариации.

Третья группа объединяет в себе показатели, называющиеся структурными характеристиками вариационного ряда. Статистические показатели из этой группы характеризуют как расположение значений изучаемого признака на числовой оси, так и характер распределения изучаемой случайной величины.

2.1.Средние величины

Как уже отмечалось выше, средние величины указывают то значение, вокруг которого группируются величины изучаемого признака. Средние величины могут быть степенными, которые будут рассматриваться в данном разделе, и структурными, которые мы рассмотрим вместе с остальными структурными характеристиками вариационных рядов.

Все степенные средние могут быть заданы с помощью формулы

38

где x – средняя величина; xi – варианта; n – число наблюдений, для

которых вычисляют среднюю.

Средние величины характеризуют различные свойства изучаемой совокупности данных. Свойство, представляемое какойлибо из средних, называется определяющим. Это понятие впервые было введено А. Я. Боярским. Наиболее распространенной средней величиной является среднее арифметическое. Определяющее свойство для этой средней заключается в том, что если каждое наблюдение в выборке заменить средней арифметической, то сумма результатов наблюдений не изменится, т. е.

где xi – i-тое наблюдение; x – средняя арифметическая; n – объем выборки. Учитывая, что x = const , (17) можно переписать в виде

Таким образом, мы получили формулу для вычисления средней арифметической величины.

В общем случае определяющее свойство для степенных средних заключается в том, что если каждое отдельное наблюдение заменить средней величиной, то сумма m-ных степеней наблюдений не изменится. Это можно записать в виде равенства:

где m – порядок степенной средней, xm - степенная средняя m-ного

порядка. Преобразовав выражение (19), можно получить формулу для определения степенной средней m-го порядка:

39

3.Если каждое наблюдение умножить на константу c, то среднее арифметическое изменится аналогичным образом. Действительно, если умножить левую и правую части равенства (18) на c и преобразовать правую части полученного равенства,

имеем

4.Сумма квадратов отклонений вариант от их средней арифметической величины меньше, чем сумма квадратов отклонений от любой другой величины, не равной x , т. е.

достигает минимума в точке a = x . Продифференцировав (24) по a, получим

Далее найдем, в какой точке производная от выражения (24) принимает нулевое значение:

2 ∑(xi − a) (−1) = 0 ,

откуда

∑xi − n a = 0

и

a = ∑nxi = x.

Отсюда следует, что сумма квадратов отклонений (24) имеет один локальный экстремум в точке a = x . Так как вторая производная этой функции по a в точке a = x равна положительному числу

d(2 ∑(xi − a) (−1))= 2, da

41