
Mashkovsky_Lesnaya_biometria
.pdf
ось абсцисс в точках m – 2σ и m + 2σ, то ее площадь будет равна 0,9545, а если в точках m – 3σ и m + 3σ, то 0,9973. Как известно, площадь криволинейной трапеции, ограниченной кривой плотности распределения вероятностей, осью абсцисс и прямыми x = a и x = b, равна вероятности попадания непрерывной случайной величины в интервал ]a; b[. Таким образом, случайная величина, подчиняющаяся закону нормального распределения с параметрами m и σ, с вероятностью 0,9973 попадет в интервал ] m – 3σ ; m + 3σ [. Это значит, что вероятность ее отклонения от математического ожидания m на величину, превышающую три сигмы, очень мала. Иными словами, это означает, что такое событие практически невозможно.
Это называется правилом трех сигм.
Функция нормального распределения F(x) имеет вид
x |
1 |
x |
− |
( z−m)2 |
|
F(x) = ∫P(z)dz = |
∫e |
2 σ2 dz . |
|||
−∞ |
σ 2 π −∞ |
|
|
|
|
Зная значения параметров m и σ, можно определить теоретические вероятности попадания исследуемой случайной величины в интервалы вариационного ряда (а следовательно, и его теоретические частоты), исходя из предположения, что она подчинена закону нормального распределения. Это позволит изобразить графически кривую нормального распределения и сравнить теоретические и эмпирические частоты вариационного ряда, на основании чего можно будет решить, следует эмпирическое распределение нормальному закону или нет.
Как отмечалось выше, вероятность попадания случайной величины в какой-нибудь интервал равна
P(a < X < b) = F(b) − F(a),
где F(x) – функция распределения, a и b – границы интервала.
Для нормального распределения это можно записать следующим образом:
P(a < X < b) =
= |
|
1 |
∫e− |
( z−m)2 |
1 |
∫e− |
( z−m)2 |
(94) |
||
|
2 σ2 dz − |
2 σ2 dz. |
||||||||
|
|
|
b |
|
|
|
a |
|
|
|
|
σ |
2 π −∞ |
|
|
σ 2 π −∞ |
|
|
|
||
Интегралы, входящие в это выражение, нельзя выразить через элементарные функции, но их можно вычислить через специальную функцию
92

|
1 |
x |
− |
t 2 |
|
F(x) = |
∫e |
2 |
dt, |
||
|
2 π −∞ |
|
|
|
|
которая является интегральной функцией нормального распределения с параметрами m = 0 и σ = 1. Для этого следует перейти к нормированной случайной величине:
T = X σ−m .
Преобразовав неравенство a ≤ X < b соответствующим образом, получим
a −σm ≤ X σ− m < b −σm .
Эти два неравенства равносильны, следовательно, их вероятности равны между собой:
|
|
|
|
|
|
|
|
|
a − m |
|
|
X − m |
|
a − m |
|
|
|||||||||||||||
P(a ≤ X < b) = P |
|
|
|
|
|
≤ |
|
|
|
|
|
|
< |
|
|
. |
|
|
|||||||||||||
σ |
|
|
|
σ |
|
|
|
σ |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Используя (95) и (94), получим |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a − m |
|
|
X − m |
|
a − m |
|
|
|||||||||||||||
P(a ≤ X < b) = P |
|
|
|
|
|
≤ |
|
|
|
|
|
|
< |
|
|
= P(t1 ≤T < t2 ) = |
|||||||||||||||
σ |
|
|
|
σ |
|
|
|
σ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
b |
−( z−m)2 |
|
|
|
|
1 |
|
|
|
a |
−( z−m)2 |
|
|
|||||||||||||
= |
σ |
2 |
π |
∫e |
|
2 σ2 |
dz − |
σ |
2 π |
∫e |
|
|
2 σ2 |
dz = |
|||||||||||||||||
|
−∞ |
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|||||||||||||
|
z − m |
|
|
|
|
|
|
|
|
|
|
|
b−m |
|
|
t 2 |
|
|
|
|
|
|
|
a−m |
|
t 2 |
|||||
|
= t = |
1 |
|
|
|
|
σ |
|
|
|
|
|
1 |
|
|
σ |
|||||||||||||||
= σ |
|
|
|
∫ |
|
e− |
|
dz − |
|
∫ e− |
|
dz = |
|||||||||||||||||||
|
2 |
|
2 |
||||||||||||||||||||||||||||
|
dz |
= σ dt |
|
|
|
|
2 π |
|
|
|
−∞ |
|
|
|
|
|
|
|
2 π |
|
−∞ |
|
|
||||||||
|
1 |
t2 |
|
− |
t 2 |
|
|
|
|
|
|
1 |
|
|
|
t1 |
− |
t 2 |
|
|
|
|
|
|
|
|
|
||||
= |
∫e |
|
dz − |
|
|
|
|
|
∫e |
2 dz = Φ(t2 ) −Φ(t1 ) . |
|||||||||||||||||||||
2 |
π |
2 |
|
|
|
|
2 π |
|
|||||||||||||||||||||||
|
−∞ |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(95)
(96)
Используя (96) и статистические таблицы, мы можем вычислить теоретические частоты вариационного ряда, предполагая, что исследуемая случайная величина распределена по нормальному закону.
Выполним эту работу для вариационных рядов по диаметру и высоте, приведенных в табл. 12 и 13. Для вычислений составим вспомогательную таблицу (табл. 26). С учетом того, что оценкой параметров нормального распределения методом моментов являются
93

среднеквадратическое отклонение и среднее арифметическое, вычислим нормированные нижнюю и верхнюю границы интервалов следующим образом:
|
|
|
|
x |
− λ − x |
|
|
x |
i |
+ λ |
− x |
|
|
|
|
|
|
|
|
|
|||
|
н |
|
|
i |
2 |
|
в |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ti |
= |
|
|
|
|
; |
ti = |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Таблица 26. Вычисление теоретических частот для функции |
||||||||||||||||||||||
|
нормального распределения (диаметры) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
xi |
|
|
fi |
|
н |
|
в |
|
|
н |
|
в |
) |
|
Pi |
|
~ |
|
~ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
ti |
|
ti |
|
Ф(ti ) |
|
Ф(ti |
|
|
fi |
|
= fi − fi |
|
|||||||
|
14,45 |
|
0 |
|
–2,52 |
|
–2,09 |
|
0,000 |
|
|
0,018 |
|
0,018 |
|
3,6 |
|
–3,6 |
|
||||
|
17,65 |
|
3 |
|
–2,09 |
|
–1,66 |
|
0,018 |
|
|
0,048 |
|
0,030 |
|
6,0 |
|
–3,0 |
|
||||
|
20,85 |
|
11 |
|
–1,66 |
|
–1,23 |
|
0,048 |
|
|
0,106 |
|
0,058 |
|
11,6 |
|
–0,6 |
|
||||
|
24,05 |
|
29 |
|
–1,23 |
|
–0,80 |
|
0,106 |
|
|
0,212 |
|
0,106 |
|
21,2 |
|
7,8 |
|
||||
|
27,25 |
|
39 |
|
–0,80 |
|
–0,37 |
|
0,212 |
|
|
0,356 |
|
0,144 |
|
28,8 |
|
10,2 |
|
||||
|
30,45 |
|
32 |
|
–0,37 |
|
0,06 |
|
0,356 |
|
|
0,524 |
|
0,168 |
|
33,6 |
|
–1,6 |
|
||||
|
33,65 |
|
33 |
|
0,06 |
|
0,49 |
|
0,524 |
|
|
0,688 |
|
0,164 |
|
32,8 |
|
0,2 |
|
||||
|
36,85 |
|
23 |
|
0,49 |
|
0,92 |
|
0,688 |
|
|
0,821 |
|
0,133 |
|
26,6 |
|
–3,6 |
|
||||
|
40,05 |
|
10 |
|
0,92 |
|
1,35 |
|
0,821 |
|
|
0,911 |
|
0,090 |
|
18,0 |
|
–8,0 |
|
||||
|
43,25 |
|
9 |
|
1,35 |
|
1,78 |
|
0,911 |
|
|
0,961 |
|
0,050 |
|
10,0 |
|
–1,0 |
|
||||
|
46,45 |
|
3 |
|
1,78 |
|
2,21 |
|
0,961 |
|
|
0,986 |
|
0,025 |
|
5,0 |
|
–2,0 |
|
||||
|
49,65 |
|
4 |
|
2,21 |
|
2,64 |
|
0,986 |
|
|
0,996 |
|
0,010 |
|
2,0 |
|
2,0 |
|
||||
|
52,85 |
|
2 |
|
2,64 |
|
3,07 |
|
0,996 |
|
|
0,999 |
|
0,003 |
|
0,6 |
|
1,4 |
|
||||
|
56,05 |
|
2 |
|
3,07 |
|
3,49 |
|
0,999 |
|
|
1,000 |
|
0,001 |
|
0,2 |
|
1,8 |
|
||||
|
59,25 |
|
0 |
|
3,49 |
|
3,92 |
|
1,000 |
|
|
1,000 |
|
0,000 |
|
0,0 |
|
0,0 |
|
||||
|
Сумма |
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,000 |
|
200,0 |
|
0,0 |
|
||
В отличие от анализируемого вариационного ряда, нормальное распределение определено на интервале от –∞ до +∞. Для того чтобы области определения эмпирического и нормального распределения сделать одинаковыми, добавим дополнительные интервалы перед первым интервалом с границами от –∞ до нижней границы первого интервала и после последнего интервала с границами от верхней границы последнего интервала до +∞. Эмпирические частоты этих дополнительных интервалов будут равны нулю, так как в исходных данных нет ни одного наблюдения, которое было бы меньше нижней границы первого интервала или больше верхней границы последнего интервала. Значения функции нормированного нормального распределения для нижней Ф(tiн) и верхней Ф(tiв) границ интервалов можно найти с помощью табл. 2 приложения, используя в качестве
94

аргументов значения tiн и tiв соответственно. В этой таблице значения функции распределения даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует воспользоваться соотношением Ф(–x) = 1 – Ф(x), которое справедливо, так как нормальное распределение является симметричным.
Вероятности для интервалов вариационного ряда легко вычислить как разность значений функции распределения для верхней и нижней границ:
Pi = Φ(tiв) −Φ(tiн) .
Теперь можно найти теоретические частоты ряда: fi = n Pi .
Аналогичным образом можно вычислить теоретические частоты для вариационного ряда высот (табл. 27).
Таблица 27. Вычисление теоретических частот для функции
нормального распределения (высоты)
|
xi |
|
fi |
|
н |
|
в |
|
н |
|
в |
) |
|
Pi |
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
ti |
|
ti |
|
Ф(ti ) |
|
Ф(ti |
|
|
fi |
|
= fi − fi |
|
||||
|
16,05 |
|
0 |
|
–4,02 |
|
–3,59 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
|
17,05 |
|
2 |
|
–3,59 |
|
–3,15 |
|
0 |
|
0,001 |
|
0,001 |
|
0,2 |
|
1,8 |
|
|
|
18,05 |
|
1 |
|
–3,15 |
|
–2,72 |
|
0,001 |
|
0,003 |
|
0,002 |
|
0,4 |
|
0,6 |
|
|
|
19,05 |
|
4 |
|
–2,72 |
|
–2,28 |
|
0,003 |
|
0,011 |
|
0,008 |
|
1,6 |
|
2,4 |
|
|
|
20,05 |
|
5 |
|
–2,28 |
|
–1,85 |
|
0,011 |
|
0,032 |
|
0,021 |
|
4,2 |
|
0,8 |
|
|
|
21,05 |
|
2 |
|
–1,85 |
|
–1,41 |
|
0,032 |
|
0,079 |
|
0,047 |
|
9,4 |
|
–7,4 |
|
|
|
22,05 |
|
13 |
|
–1,41 |
|
–0,98 |
|
0,079 |
|
0,164 |
|
0,085 |
|
17,0 |
|
–4 |
|
|
|
23,05 |
|
25 |
|
–0,98 |
|
–0,54 |
|
0,164 |
|
0,295 |
|
0,131 |
|
26,2 |
|
–1,2 |
|
|
|
24,05 |
|
31 |
|
–0,54 |
|
–0,11 |
|
0,295 |
|
0,456 |
|
0,161 |
|
32,2 |
|
–1,2 |
|
|
|
25,05 |
|
32 |
|
–0,11 |
|
0,33 |
|
0,456 |
|
0,629 |
|
0,173 |
|
34,6 |
|
–2,6 |
|
|
|
26,05 |
|
43 |
|
0,33 |
|
0,76 |
|
0,629 |
|
0,776 |
|
0,147 |
|
29,4 |
|
13,6 |
|
|
|
27,05 |
|
24 |
|
0,76 |
|
1,2 |
|
0,776 |
|
0,885 |
|
0,109 |
|
21,8 |
|
2,2 |
|
|
|
28,05 |
|
14 |
|
1,2 |
|
1,63 |
|
0,885 |
|
0,948 |
|
0,063 |
|
12,6 |
|
1,4 |
|
|
|
29,05 |
|
3 |
|
1,63 |
|
2,07 |
|
0,948 |
|
0,981 |
|
0,033 |
|
6,6 |
|
–3,6 |
|
|
|
30,05 |
|
1 |
|
2,07 |
|
2,5 |
|
0,981 |
|
0,994 |
|
0,013 |
|
2,6 |
|
–1,6 |
|
|
|
31,05 |
|
0 |
|
2,5 |
|
2,94 |
|
0,994 |
|
1 |
|
|
0,006 |
|
1,2 |
|
–1,2 |
|
|
Сумма |
|
200 |
|
|
|
|
|
|
|
|
|
|
1,000 |
|
200,0 |
|
0,0 |
|
Последние колонки табл. 26 и 27, представляющие собой разность между эмпирическими и теоретическими частотами, дают нам информацию о близости теоретического (в данном случае
95
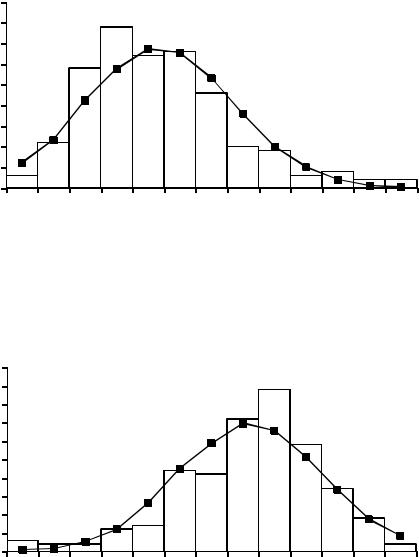
нормального) и эмпирического распределений. Однако по данным отклонениям достаточно трудно принять решение о согласованности эмпирического и теоретического распределений. Более наглядную картину можно увидеть, изобразив эти распределения графически
(рис. 14 и 15).
|
45 |
|
|
40 |
|
|
35 |
|
частоты |
30 |
|
25 |
|
|
20 |
|
|
15 |
|
|
|
|
|
|
10 |
|
|
5 |
|
|
0 |
|
|
17,6520,8524,0527,2530,4533,6536,8540,0543,2546,4549,6552,8556,05 |
|
|
значения классов |
. |
Рис. 14. Сравнение эмпирического и нормального распределений сосновых |
||
|
стволов по диаметрам |
|
|
50 |
|
|
45 |
|
|
40 |
|
частоты |
35 |
|
30 |
|
|
25 |
|
|
20 |
|
|
|
15 |
|
|
10 |
|
|
5 |
|
|
0 |
|
|
17,4518,4519,4520,4521,4522,4523,4524,4525,4526,4527,4528,4529,45 |
|
|
значения классов |
. |
Рис. 15. Сравнение эмпирического и нормального распределений сосновых |
||
|
стволов по высотам |
|
96
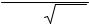
Однако такие сравнения распределений будут субъективными. Для того чтобы дать объективную оценку согласованности эмпирических и теоретических распределений, необходимо воспользоваться специальными методиками проверки статистических гипотез.
3.5.Некоторые распределения, используемые в лесном
хозяйстве
Наряду с нормальным, в лесном деле используется еще целый ряд непрерывных распределений случайных величин. Рассмотрим некоторые из них.
Логнормальное распределение – это распределение случайной величины X, логарифм которой подчинен закону нормального распределения.
Область значений 0 ≤ x < +∞.
Функция плотности вероятности (рис. 16):
|
|
|
|
|
x 2 |
|
|
|
|
|
− log |
|
|
|
|
|
|
|
|||||
P(x) = |
1 |
exp |
|
m |
. |
||
|
|
|
|
|
|||
|
x σ 2 π |
|
|
2 σ2 |
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
97
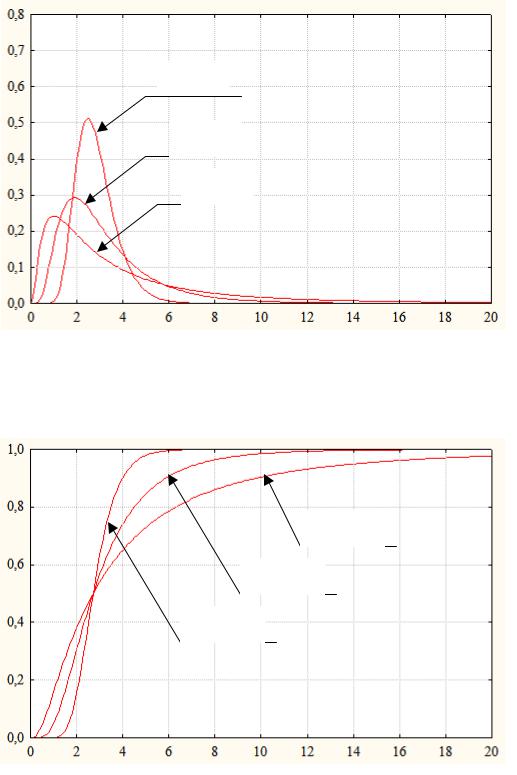
σ = 0,3
σ = 0,6
σ = 1,0
Рис. 16. Плотность распределения вероятностей (m = 1)
Функция распределения вероятностей для различных значений параметра σ и m = 1 приведена на рис. 17.
σ = 1,0
σ = 1,0
σ = 1,0
Рис. 17. Функция распределения вероятностей (m = 1)
98
Оценка параметров: m = exp(μ) ;
∑n (log(xi ) − μ)2
σ2 = |
i=1 |
|
|
|
|
, |
|
|
|
n − |
1 |
||||
|
|
|
|
|
|||
где |
|
|
|
|
|
||
|
n |
|
|
|
|
|
|
|
∑log(xi ) |
|
|
||||
μ = |
i=1 |
|
|
. |
|
|
|
|
n |
|
|
|
|||
|
|
|
|
|
|
|
|
Гамма-распределение
Область значений 0 ≤ x < +∞.
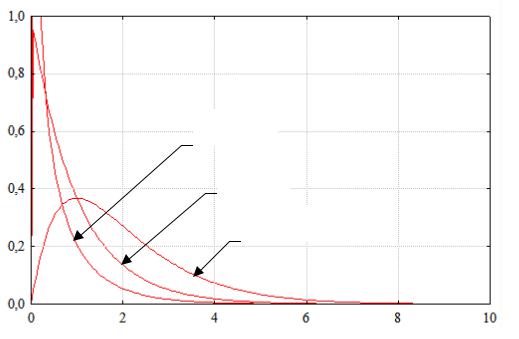
Функция плотности вероятности (рис. 18):
|
|
|
|
|
|
x |
|
|
|
x |
c−1 |
exp |
− |
|
|
|
|
||
b |
|
||||||||
|
|
|
|
|
|||||
P(x) = |
|
|
|
|
|
|
|
|
, |
|
b Γ(c) |
|
|||||||
b |
|
|
|
||||||
∞
гдеΓ(c) = ∫exp(−u) uc−1 du – гамма-функция.
0
c = 0,5
c = 1
c = 2
Рис. 18. Плотность распределения вероятностей (b = 1)
99
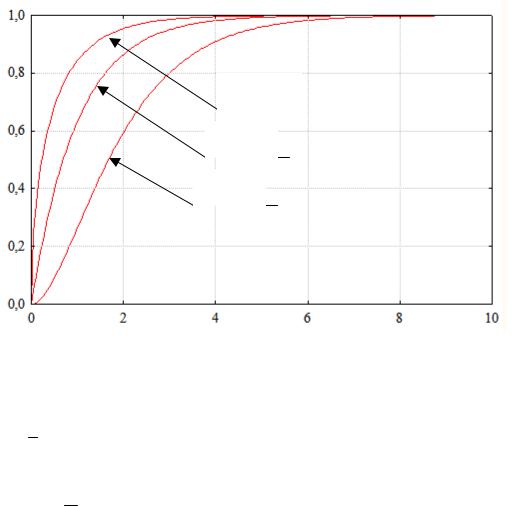
На рис. 19 приведена функция распределения вероятностей для различных значений параметра c и b = 1.
c = 0,5
c = 1
c = 2
Рис. 19. Функция распределения вероятностей (b = 1)
Оценка параметров:
b= S 2 ; x
c= x 2 ,
S
где x – выборочное |
среднее; S 2 – выборочная дисперсия |
(без |
||||
поправки). |
|
|
|
|
|
|
Бета-распределение |
|
|
||||
Функция |
плотности |
вероятности (рис. 20, 22 и |
24): |
|||
P(x) = |
xv−1 (1 − x)w−1 |
0 ≤ x ≤ 1, v > 0, w > 0,где B(v,w) – бета- |
||||
|
|
|
, |
|||
|
Β(v, w) |
|
||||
функция с параметрами v, w, задаваемая формулой:
1
Β(v, w) = ∫uv−1 (1 − u)w−1 du.
0
100
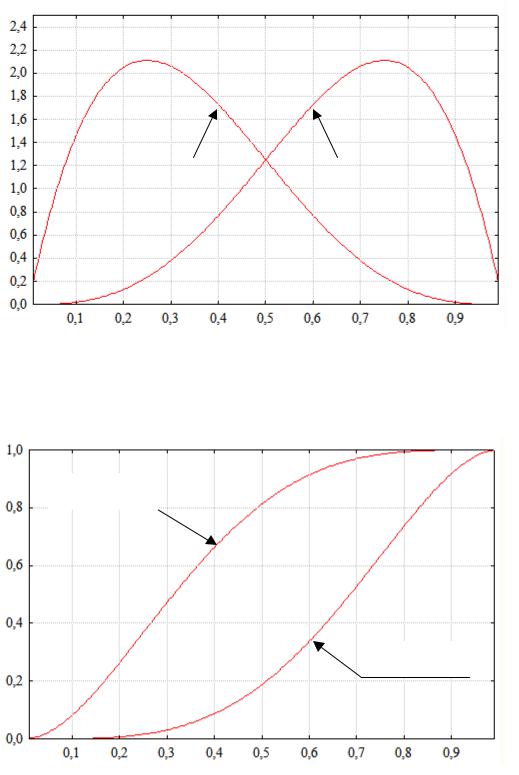
v = 2, w = 4 |
|
v = 4, w = 2 |
|
|
|
Рис. 20. Плотность распределения вероятностей
Вид функций распределения вероятностей для различных значений параметров v и w приведена на рис. 21, 23 и 25.
v = 2, w = 4
v = 4, w = 2
Рис. 21. Функция распределения вероятностей
101
