25 Математическая модель управления запасами в деревообработке

Для ее характеристики принимаются допущения:

1запас расходуется равномерно с постоянной интенсивностью

2пополняется мгновенно, а дефицит запаса не допустим.

Т – плановый период

Постановка задачи: имеется предприятие, для нормального функционирования необходимы производственные запасы. Эти запасы поставляются одномоментно, достигая некоторой максимальной величины, а затем расходуются равномерно с темпом, соответствующему темпу их потребления производством. В момент расходования запасы пополняются до исходного объема. Известны: общая потребность в сырье и материалах данного вида, продолжительность планового периода, затраты, связанные с пополнением и хранением запасов. При этом часть издержек пропорциональна объему запаса, а др. часть - числу пополнения.

Требуется определить оптимальн. значение объема однократного пополнения , минимализирующие общие издержки предприятия.

Для построения матем. модели введем обозначения:

V-общая потребность предприятия в запасах данного вида на плановый период.

T- продолжительность планового периода.

С- оптовая цена единицы запаса данного вида.

γ-коэф. характеризующий затраты на хранение единицы запаса.

С_о-затраты на однократное пополнение, не зависящее от объема запаса(тел. разговоры и т. д .).

К- коэф. учитывающий затраты на пополнение, зависящий от объема запаса (транспорт, погрузочно-разгрузочные затраты на единицу объема).

q-объем однократного пополнения

n- число пополнений в течение планового периода

t_н- интервал времени между 2-мя последовательными пополнениями.

Общие издержки:

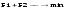
F1-затраты на хранение, F2- затраты на пополнение.

- однократное пополнение.

;

Воспользуемся необходимыми условиями экстремума:

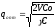- оптимальный объем партии

- достиг. min

1 . Методология имитационного моделирования.ИМ – процесс изучения объектов путем проведения экспериментов на их мат. моделях, реализуемых на ЭВМ. Сущность метода: описывая вз-вие составных частей исследуемой системы с помощью мат. соотношений, м. получить небх. о ней инфо, не обращаясь к натуральным экспериментам.При разработке имитационных маделей рекомендуется следовать трем правилам: 1). участие в создании модели специалистов, которые впоследствии должны ее использовать; 2). поэтапность внедрения, т.к. в практической деятельности могут найти применение отдельные блоки имитационной модели для исследования вопросов, связанных с изучаемой проблемой; 3). доступность, пользователь должен получать результаты вычислительного эксперимента в привычной для него форме: в виде таблиц, графиков, гистограмм.

Области применения ИМ. ИМ используется при решении следующих задач:

1. теоретических (математика, физика, химия).Напр., вычисление площадей фигур, ограниченных кривыми;

2.практических задач организованного управления:

- задачи производственно-технологических процессов (в сфере управления запасами, при создании СМО). Известны имитацион. модели таких устройств как прокатный стан, химический реактор, а также модели форм и отраслей промышленности.

-задачи систем экономического характера (процессы планирования, экономич. прогнозирования, инвестицион. процессы). ИМ целесообразно применять там, где недопустимо участие людей (исслед-ие воз-вия лекарств на организм чел-а, ход боевых действий). Осн. этапы построения ИМ-ей объекта:

1Постановка задачи и определение целей эксперимента.Рассм-ся вар-ты тех. схем, типы взаимозаменяемого оборуд-ния, виды сырья и способы его подготовки, кот. б. приняты для сопоставительного анализа. Устан-ся инфо, необх. для проведения исследований. Опр-ся параметры, кот. должны войти в ИМ-ль в кач-ве вход. и выход. переменных. Дается качествен. описание их взаимосвязи и др.

2Изучение исследуемого явления. Концептуальная модель – модель абстрактного, описательного типа, отраж. представление (концепцию) исследователя о сущ-ти процесса ф-ния исслед-го объекта при рассм-нии этого процесса в границах, определяемых целями исследования. Изучение процесса ф-ния объекта в установлен. границах – наблюдение за объектом, если объект реально существует в теч. достаточ. длитель. времени. Ознакомление с документацией по объекту. Консультации со специалистами, проектировщиками и др. В результате уточняются вход. и выход. данные и ограничения., устанавл-ся критерии , с помощью кот. б. оценив-ся эф-ть ф-ния системы. Результаты проверенного изучения объекта систематизир-ся и излагаются и в словесной форме и в графическом виде.

1. Планирование эксперимента (ПЭ). Предшествует проведению эксперимента. Стратегическое П – ПЭ, кот. должно дать необх. инфо. Тактичес. П – опр-ие способа проведения каждой серии испытаний, предусмотрен. планом эксперимента. Экспериментирование – с целью получения желаемых данных.

2. Формализация (ф-я) мат. модели (выделение главных факторов и исключение второстепенных). Система разбивается на блоки. Ф-ся з-ны моделирования и правдоподоб. гипотезы относ-но поведения как системы вцелом, так и отдель. ее блоков. При это м в каждом блоке для их описании м. исп-ся свой мат. аппарат (графики, схемы и др.). В 1 блок объед-ся родствен., т.е. преобр-ся по близким правилам компоненты. Ф-ую мат. модель графически представляют в виде блрок-схемы, наз. алгоритмом процесса.

3. Составление машинной программы. Выбор языка программирования + генерирование послед-ти случ. чисел, имеющих задан. распределение.

4. Проверка мат. модели на адекватность. Провер-ся наличие принципиаль. (ПО) и технич. ошибок (ТО). ПО – неправиль. выбор списка переменных, невер. гипотеза, связывающ, переменные. ТО – обр-ся при составлении программы (их находят локальной проверкой по этапам блоком программы).

5. Проведение эксперимента и обработка результатов. Эксперимент вып-ся в диалоговом режиме. Обработка результатв проводится методами мат. статистики, н-р с исп-ем регрессион., кореляцион., дисперсион. анализа.