6Задача нелинейного программирования. Методы решения и оптимизации.

Задачи отыскания наибольшего или наименьшего значения целевой функции на множестве допустимых планов носят название экстремума задач. Такие задачи называются задачами нелинейного программирования. При линейном программировании принимают, что производство каждой детали приносит определённые одинаковые издержки. На самом деле – чем больше деталей, тем меньше издержек, то есть затраты на каждое изделие, это некая функция. Решения данных задач проводиться по необходимым и достаточным условиям экстремума. Если одна переменная, то по методам: градиентный, метод дихотомии (половины деления), метод золотого сечения. Если функция нескольких переменных: метод покоординатного поиска, градиентный метод, необходимое и достаточное условие экстремума.

7 Многокритериальные задачи исследования операцийЗадачи исследования операций, решения которых направлены на оптимизацию нескольких показателей, наз-ся многокритериальными (МК)

Вар-ты формирования критериев МК задач:

1Из всех рассматриваемых критериев выделяется важнейший, по которому решается задача. На остальные критерии накладываются ограничения в тех пределах, в которых хотел бы иметь разработчик, исполнитель, заказчик.

Пример:W₁, W₂, W₃, ….. W_n . W₁ → max; W₂≥W₂⁰, W₃≥W₃⁰, W_n≥W_n⁰.

2Формируется обобщенный критерий, представляющий собой функцию от частных критериев. Предполагается, что все критерии имеют одну размерность и диапазоны измнения. Обобщен. критерий представляют в виде дроби. Числитель в ней – все частн. Критерии, кот-е надо обратить в МАХ-м, а в знаменателе – произведение MIN-х критериев. W=W₁W₂W₃/W₄W₅. Недостаток: м.б. достигнуто приемлемое значение обобщенных критериев при неудовлетворительных значениях некот-х частных критериев.

1Формируется обобщенный критерий W в виде взвешенной суммы частных критериев:

λ_i – коэф-т значимости соотв-го критерия W_i. Он берется с «+», если частный критерий W_i обращается в МАХ-м, с минусом – в MIN-м. Абсолютные величины коэф-та λ_i берутся пропорциональными важности соответствующего частного критерия с учетом требован6ия их нормированности : . Оценка ведется экспертным методом.

2Формируется критерий при оценке качественных показателей: эстетич. требования к внешнему виду, технологичность конструкции, удобство эксплуатации.

Пример:требуется рекомендовать производству один из нескольких имеющихся проектов корпусной мебели. При определении лучшего варианта учит-т все показатели качества. Для перехода к количественному показателю W_i противопоставляется количественный показатель d_i, изменяющийся от 0 до 1. Если, напрмер, качеств. Критерий приеимает 3 значения: «плохо», «удовл.», «хорошо», то соответствующий этим оценкам количествен. показатель будет:

; ;.

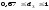Совокупный показатель

«+» расчета: область значений совокупного показателя D измен-ся от 0 до 1. Если хоть один из показ-лей d_i =0, то D=0.

8 Симплекс-метод в задачах линейного программирования. Признак оптимальности опорного решения.Идея метода:

1) указывает способ вычисления исходной программы;

2)Устанавливаем признак позволяющий проверять данную программу на оптимальность;

3)указывает способ, позволяющей на данной программе выбрать другую, более близкую к оптимальной.

Сj- коэф. Целевой функции; Сi- коэф. Целевых функций при базисных неизвестных; Р – наименование базисных неизвестных; В – неотрицательные значения ограничений; β – симплексное отношение, показывающее величину отношения значений ограничений в столбце В к элементам аij в разрешающем столбце; W – значение целевой функции; ∆ij – двойственная оценка. Для решения необходимо:

1) заполнить первую симплекс-таблицу.

2) рассчитать в каждом столбце двойственные оценки.

3) если на макс то разрешающий столбец отрицательная оценка, если мин то положительная,

4) найти симплексное отношение в каждом ряду. Выбрать наименьшую Экономический смысл: в столбце В представлены ресурсы, в разрешающем столбце – нормы их расхода. В результате деления В на разр получаем количество продукции, которое можно изготовить из данных ресурсов.

5) выбирают разрешающий элемент

6) пересчёт таблицыПризнаком оптимальности опорного решения является отсутствие отрицательных двойственных оценок при решении задач максимизации или отсутствие положительных двойственных оценок при решении задач минимизации.

9 Математическая модельПо форме представления информации делятся на детерминированные и вероятностные. Детерминир. модели предсказывают значние выходной величины при заданных значениях входных параметров. Они строятся на основе фундаментальных теоретических законов и закономерностей. Это з-ны термодинамики, химич. кинетики и т.д. Вероятностные модели содержат случайные параметры, поэтому рез-тат расчета по такой модели это либо вероятность наступления определен. События, либо статистическая оценка некот-х случайных величин. Все регрессион. модели явл-ся вероятностными, т.к. для них выходной величиной явл-ся статистическая оценка условного математ. ожидания некот. параметра.

По способу получения информации дел-ся на аналитические и эмпирические. Аналитические модели получают теорет. путем, но при построении их используют константы, значения кот-х определяют по рез-там эксперимента. Эмпирические модели получ-т по рез-там обработки экспериментальных данных.

По фактору времени: статические, динамические. Статич. модели включают описание связи между основными процесса в установившихся режимах, т.е. в равновесн. состоянии без изменения во времени. Динамические модели характеризуются множеством переменных состояния системы, кот-е изменяются во времени.