1Уравнение неразрывности для носителей заряда в проводнике. Дифференциальная форма условия существования постоянного электрического тока

В электродинамике уравнение непрерывности выводится из уравнений Максвелла. Оно утверждает, что дивергенция плотности тока равна изменению плотности заряда со знаком минус

Вывод Закон Ампера гласит Взяв дивергенцию от обеих частей выражения, получим но дивергенция ротора равняется нулю, таким образом

По теореме Гаусса Подставляя это выражение в предыдущее уравнение, получаем искомое уравнение непрерывности.

2 Энергия магнитного поля контура с током. Энергия магнитного поля соленоида. Плотность энергии магнитного поля

Увеличение тока в проводнике вызывает соответствующее усиление его магнитного поля, которое, подобно электрическому полю, обладает энергией. Найденная нами собственная энергия тока в контуре есть не что иное, как энергия Wm магнитного поля этого контура g током. В качестве примера рассмотрим однородное магнитное поле длинного соленоида, индуктивность которого . где V — объем поля соленоида. Магнитная индукция поля соленоида выражается формулой, откудаПодставив эти значения для L иI найдем энергию магнитного

поля длинного соленоида: (однородное поле)(неоднородное)

энергетическое определение индуктивности: индуктивность контура численно равна удвоенной энергии магнитного поля, создаваемого проходящим по контуру током единичной поток самоиндукции Поэтому энергию магнитного поля этого контура

Билет21

1 Правела Кирхгофа для расчета разных электрических цепей

Первое правило Кирхгофа выражает условие постоянства тока в цепи и вытекает из того, что в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. Назовем узлом любую точку разветвления цепи, т.е. любую точку, в которой сходится больше двух проводников. Тогда первое правило Кирхгофа можно сформулировать следующим образом: алгебраическая сумма токов, сходящихся в узле, равна нулю: При этом токи, подходящие к узлу, считают положительным и, а токи, отходящие от него, — отрицательными

Второе правило Кирхгофа является обобщением закона Ома на разветвленные электрические цепи. Оно состоит в следующем: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Iк на сопротивления Rk соответствующих участков этого кон- тура равна алгебраической сумме э.д.с. k в контуре:.

2 Диа и парамагнетики. Элементарная теория диамагнетизма

Диамагнетиками называются вещества, магнитные моменты атомов или молекул которых при отсутствии внешнего магнитного поля равны нулю. Иначе говоря, в атомах или молекулах диамагнитных веществ векторная сумма орбитальных магнитных моментов всех электронов равна нулю. Диамагнетиками являются инертные газы, большинство органических соединений, многие металлы (висмут, цинк, золото, медь, серебро, ртуть и др ), смолы, вода, стекло, мрамор.При внесении диамагнитного вещества в магнитное поле в каждом его атоме наводится магнитный момент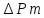, направленный противоположно вектору В индукции магнитного поля. Если векторная сумма орбитальных магнитных моментов всех электронов атома (или молекулы) не равна нулю, то атом в целом обладает некоторым магнитным моментомVm. Такие атомы (молекулы) называются парамагнитными, а состоящие из них вещества — парамагнетиками. К парамагнетикам относятся кислород, окись азота, алюминий, платина, редкоземельные элементы, щелочные и щелочно- земельные металлы и другие вещества.