- •2. Закон Био-Савара-Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
- •1. Применение теоремы Остроградского-Гаусса для расчета электрических полей
- •1. Поляризация диэлектриком, виды поляризации. Поляризованность. Диэлектрическая проницаемость
- •2. Поток индукции магнитного поля. Теорема Гаусса для потока вектора индукции магнитного поля.
- •2. Сила ампера. Сила взаимодействия параллельных линейных проводников с током
- •1. Условия для напряжоности электрического поля и электрического смещения на границе раздела двух иеэлектрических сред.
- •2. Магнитные цепи. Магнитодвижущая сила. Магнитное сапротивление.
- •2 Циркуляция вектора напряженности магнитного поля. Расчет магнитного поля линейного проводника с током
- •1 Взаимная электроемкость двух тел. Электроемкость уединенного проводника. Электроемкость плоского конденсатора
- •2 Магнитный момент атома. Орбитальные и спиновые моменты электрона. Гиромагнитное отношение для орбитального и спинового моментов. Намагниченность
- •1 Энергия заряженного конденсатора. Плотность энергии электрического поля
- •2 Ферромагнетики. Кривая намагничивания. Магнитный гистерезис
- •1 Потенциальная энергия системы неподвижных зарядом
- •2 Циркуляция напряженности магнитного поля. Расчет магнитного поля тароида и соленоида
- •1Диполь электрическом поле. Момент сил, действующих на диполя в неоднородном поле
- •2 Связь между индукцией и напряжености магнитного поля в веществе. Магнитная восприимчивость магнитная проницаемость
- •1 Применение теоремы Остроградского-Гаусса для расчета электрических полей
- •2 Сила Лоренса . Уравнение движения заряженной частицы в магнитных и электрических полях
- •1Применение теоремы Остроградского –Гаусса для расчета напряженности электрического поля (поле и потенциал равномерно заряженной проводящей сферы)
- •1 Закон Видемана-Франца. Вывод закона Видемана-Франца на аснове классических предстовлений
- •1 Мощность выделяемая в цепи переменного тока
- •2 Электрический излучаемый диполь как система движущих зарядов. Интенсивность излучения электрического диполя
- •1 Закон Ома в дифференциальной форме. Вывод закона Ома на основе классической теории.
- •2Явление самоиндукции. Правело ленца. Потокосцепление. Индуктивность
- •1Уравнение неразрывности для носителей заряда в проводнике. Дифференциальная форма условия существования постоянного электрического тока
- •2 Энергия магнитного поля контура с током. Энергия магнитного поля соленоида. Плотность энергии магнитного поля
- •1 Правела Кирхгофа для расчета разных электрических цепей
- •2 Диа и парамагнетики. Элементарная теория диамагнетизма
- •1Работа электрического поля. Теорема о циркуляции вектора напряженности электрического поля
- •2Переходные процессы в электрической цепи при подключении и отключении источника тока
- •1 Свободные затухающие колебания в контуре с активным сопротивлением
- •2 Принцип действия циклических ускорителей заряженных частиц
- •1Вынужденые электрические колебания. Расчет цепи переменного тока с последовательно включенными сопротивлением, индуктивностью и емкостью методом векторной диаграммы
- •2 Плотность энергии электромагнитного поля
- •1 Закон джоуля-ленца в интегральной и дифференциальной форме
- •2 Основные свойства электромагнитных волн. Опыты Герца
- •1Ток смещения
- •2Работа перемещения проводника с током в магнитном поле
- •1 Квазистационарные токи. Условия квазистационарности цепи переменного тока
- •2 Поток энергии электромагнитного поля. Вектор умова- пойнтинга
- •1 Эффект Холла и его применение в технике и в современных научных исследованиях
- •2 Уравнения максвелла
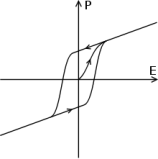
- •1 Сегнетоэлектрики. Поляризация сегнетоэлектрики. Гистерезис
- •2 Влновые уравнения. Плоская электромагнитная волна и ее свойства
- •1Условия для составляющих вектора напряженности поля и электрического смещения на границе раздела диэлектрик – проводник
- •2 Излучение диполя. Диаграмма направленности излучения
1 Эффект Холла и его применение в технике и в современных научных исследованиях
Постоянный
ток / пропускался через пластинку М
изготовленную из золота, и измерялась
разность потенциалов
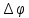 между
противолежащими точками А и С наверхней
и нижней гранях. Эти точки лежат в одном
и том же поперечном сечении проводника
М. Поэтому, как и следовало ожидать,
оказалось, что
между
противолежащими точками А и С наверхней
и нижней гранях. Эти точки лежат в одном
и том же поперечном сечении проводника
М. Поэтому, как и следовало ожидать,
оказалось, что ф
= 0. Когда пластина с гоком была помещена
в однородное магнитное поле,
перпендикулярное ее боковым граням,
то потенциалы точек А и С стали различными.
Это явление получило название явления
Холла. Было установлено, что разность
потенциалов
ф
= 0. Когда пластина с гоком была помещена
в однородное магнитное поле,
перпендикулярное ее боковым граням,
то потенциалы точек А и С стали различными.
Это явление получило название явления
Холла. Было установлено, что разность
потенциалов ф
между точками А и С пропорциональна
силе токаI,
индукции магнитного поля В и обратно
пропорциональна ширине Ь пластинки,
т. е.
ф
между точками А и С пропорциональна
силе токаI,
индукции магнитного поля В и обратно
пропорциональна ширине Ь пластинки,
т. е.
![]()
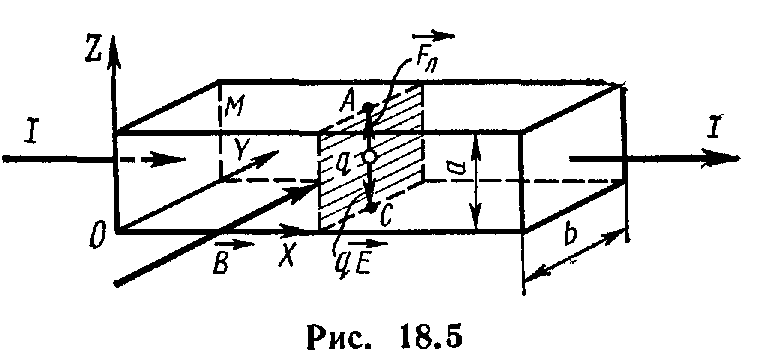 Эффект
Холла, в некоторых случаях, позволяет
определить тип носителей заряда
(электронный или дырочный) в металле
или полупроводнике, что делает его
достаточно хорошим методом исследования
свойств полупроводников.На основе
эффекта Холла работают датчики Холла:
приборы, измеряющие напряжённость
магнитного поля. Датчики Холла получили
очень большое распространение в
бесколлекторных, или вентильных,
электродвигателях (сервомоторах).
Датчики закрепляются непосредственно
на статоре двигателя и выступают в роли
ДПР (датчика положения ротора). ДПР
реализует обратную связь по положению
ротора, выполняет ту же функцию, что и
коллектор в коллекторном ДПТ.Также на
основе эффекта Холла работают некоторые
виды ионных реактивных двигателей.
Эффект
Холла, в некоторых случаях, позволяет
определить тип носителей заряда
(электронный или дырочный) в металле
или полупроводнике, что делает его
достаточно хорошим методом исследования
свойств полупроводников.На основе
эффекта Холла работают датчики Холла:
приборы, измеряющие напряжённость
магнитного поля. Датчики Холла получили
очень большое распространение в
бесколлекторных, или вентильных,
электродвигателях (сервомоторах).
Датчики закрепляются непосредственно
на статоре двигателя и выступают в роли
ДПР (датчика положения ротора). ДПР
реализует обратную связь по положению
ротора, выполняет ту же функцию, что и
коллектор в коллекторном ДПТ.Также на
основе эффекта Холла работают некоторые
виды ионных реактивных двигателей.
2 Уравнения максвелла
![]() Тем
самым было выяснено, что переменное
магнитное поле создает в проводящем
замкнутом контуре вихревое электрическое
поле. Максвелл предложил считать, что
соотношение справедливо не толь-ко для
проводящего, но и для любого замкнутого
контура, мыеленно выбранного в переменном
магнитном поле. Иными словами, он
предположил, что переменное магнитное
поле создает в любой точке пространства
вихревое электрическое поле независимо
от того, находится в этой точке проводник
или нет. Обобщенное таким образом
равенство называется первым уравнением
Максвелла в интегральной форме:
циркуляция вектора напряженности
электрического поля по про- извольному
замкнутому контуру L равна взятой в
обратным знаком скорости изменения
магнитного потока сквозь поверхность,
натянутую на контур.
Тем
самым было выяснено, что переменное
магнитное поле создает в проводящем
замкнутом контуре вихревое электрическое
поле. Максвелл предложил считать, что
соотношение справедливо не толь-ко для
проводящего, но и для любого замкнутого
контура, мыеленно выбранного в переменном
магнитном поле. Иными словами, он
предположил, что переменное магнитное
поле создает в любой точке пространства
вихревое электрическое поле независимо
от того, находится в этой точке проводник
или нет. Обобщенное таким образом
равенство называется первым уравнением
Максвелла в интегральной форме:
циркуляция вектора напряженности
электрического поля по про- извольному
замкнутому контуру L равна взятой в
обратным знаком скорости изменения
магнитного потока сквозь поверхность,
натянутую на контур.
![]() Это
равенство называется вторым уравнением
Максвелла в интегральной форме. Оно
показывает, что циркуляция вектора Н
напряженности магнитного поля по
произвольному замкнутому контуру L
равнаалгебраической сумме макротоков
и тока смещения сквозь поверхность,
натянутую на этот контур.
Это
равенство называется вторым уравнением
Максвелла в интегральной форме. Оно
показывает, что циркуляция вектора Н
напряженности магнитного поля по
произвольному замкнутому контуру L
равнаалгебраической сумме макротоков
и тока смещения сквозь поверхность,
натянутую на этот контур.
Третье
уравнение Максвелла выражает теорему
Остроградского—Гаусса для потока
вектора электрического смещения D
сквозь произвольную замкнутую поверхность
S, охватывающую суммарный свободный
заряд
![]()
Четвертое
уравнение Максвелла является обобщением
теоремы Остроградского — Гаусса на
переменное магнитное поле:
![]()
Билет29
1 Сегнетоэлектрики. Поляризация сегнетоэлектрики. Гистерезис
Сегнетоэле́ктрики
(названы по первому материалу, в котором
был открыт сегнетоэлектрический эффект
— сегнетова соль) — твёрдые диэлектрики
(некоторые ионные кристаллы и
пьезоэлектрики), обладающие в определённом
интервале температур собственным
электрическим дипольным моментом,
который может быть переориентирован
за счёт приложения внешнего электрического
поля. Сегнетоэлектрические материалы
обладают гистерезисом по отношению к
электрическому дипольному моменту.
Температура,
при которой исчезает спонтанная
поляризация (то есть собственный
дипольный момент) и происходит перестройка
кристаллической структуры, носит
название температуры (точки) Кюри (ещё
одна аналогия с ферромагнетиками).
Переход через точку Кюри означает
фазовый переход, а соответствующие
фазы обозначаются как полярная
(сегнетоэлектрик) и неполярная
(параэлектрик[1] — нелинейный диэлектрик,
не обладающий спонтанной поляризацией,
относительная диэлектрическая
проницаемость которого уменьшается с
ростом температуры).Спонтанная
поляризация в сегнетоэлектриках в
точке Кюри меняется либо непрерывно
(переход второго рода, сегнетова соль),
либо скачком (переход первого рода,
титанат бария). Другие характеристики
сегнетоэлектриков, такие как относительная
диэлектрическая проницаемость, могут
достигать в точке Кюри очень больших
значений (104
и выше).Вблизи точки Кюри в неполярной
фазе выполняется закон Кюри — Вейсса,
связывающий поляризуемость α и
температуру T сегнетоэлектрика[2]
![]() где
C и T0 — константы, определяемые видом
сегнетоэлектрика. Величина T0 носит
название температуры Кюри — Вейсса и
очень близка к значению температуры
Кюри. Если точек Кюри две, то вблизи
каждой из них в неполярной фазе
выполняется тот же закон. Вблизи верхней
— в прежней форме, а вблизи нижней — в
форме[2]:
где
C и T0 — константы, определяемые видом
сегнетоэлектрика. Величина T0 носит
название температуры Кюри — Вейсса и
очень близка к значению температуры
Кюри. Если точек Кюри две, то вблизи
каждой из них в неполярной фазе
выполняется тот же закон. Вблизи верхней
— в прежней форме, а вблизи нижней — в
форме[2]:
![]() Механизм
приобретения дипольного момента в
полярной фазе (фазе сегнетоэлектрика)
может также различаться: возможен
вариант как со смещением ионов (титанат
бария; соответствующий фазовый переход
называется переходом типа смещения),
так и с упорядочиванием ориентации уже
существующих в веществе диполей
(дигидрофосфат калия, триглицинсульфат).
Механизм
приобретения дипольного момента в
полярной фазе (фазе сегнетоэлектрика)
может также различаться: возможен
вариант как со смещением ионов (титанат
бария; соответствующий фазовый переход
называется переходом типа смещения),
так и с упорядочиванием ориентации уже
существующих в веществе диполей
(дигидрофосфат калия, триглицинсульфат).
Гистере́зис
(греч. ὑστέρησις — «отстающий») —
свойство систем (физических, биологических
и т.д.), мгновенный отклик которых на
приложенные к ним воздействия зависит
в том числе и от их текущего состояния,
а поведение системы на интервале времени
во многом определяется её предысторией.
Для гистерезиса характерно явление
"насыщения", а также неодинаковость
траекторий между крайними состояниями
(отсюда наличие остроугольной петли
на графиках). Не следует путать это
понятие с инерционностью поведения
систем, которое обозначает монотонное
сопротивление системы изменению её
состояния.