
- •2.Определение предела ф-ции на языке окрестностей:
- •3.Теорема о локальной ограниченности функции, имеющей при конечный предел
- •4.Функция называется бесконечно малой
- •5.Функция называется бесконечно большой
- •8.Понятие непрерывности функции на промежутке.
- •9.Асимптотой графика функции называется
- •12. Произв сложн ф-и
- •13. Производная обратной функции равна
- •16.Теорема Ферма.Геометрический смысл теоремы Ферма.
- •17.Теорема Ролля.Геометрический смысл теоремы Роля.
- •18.Теоремы Лагранжа и Коши.Геометрический смысл теоремы Лагранжа.
- •19.Правило Лопиталя
- •20.Сравнение роста показательной,степенной и логарифмической функций.
- •22.Разложение фу-ций по фо-ле Маклорена
- •23.Определение возрастающей(убывающей)фу-ции
- •24.Отыскание точек локального экстремума фу-ции
- •25.Алгоритм нахождения наибольшего и наименьшего значений фу-ций на отрезке
- •26. Первообразной функцией для функции f(X) называется
- •28. Алгоритм интегрирования рацион.Дробей:
- •29. Универсальная тригоном подстановка
- •32.Интегралы типа ,
- •35.Матрицей размера mxn называется
- •36. Определитель(detA)-
- •38.Рангом матрицы называется
- •39.Система линейных алгебраических уравнений—
- •41.Вектором наз.
- •42.Проекция вектора на ось
- •43.Базисом на пл-сти
- •44. Направление в-ра в пространстве
- •46.Векторным произв. *называется
- •55.Исследование общего уравнения плоскости
- •57. Прямая в пр-ве может быть задана
- •60. Цилиндрической пов-тью наз
- •61. Понятие фнп
- •64.Неявно заданная фу-ция
- •65.Линии уровня.Градиент
- •66. Точка m0(x0;y0) называется точной локального максимума(минимума) функции двух переменных
- •67.Понятие об условном экстремуме.
55.Исследование общего уравнения плоскости
Уравнение
![]() ,
где
,
где![]() ,
,![]() и
и![]() -
координаты нормального вектора
-
координаты нормального вектора![]() ,
называетсяобщим
уравнением плоскости.
,
называетсяобщим
уравнением плоскости.
 ;
из этого следует, что скалярное
произведение
;
из этого следует, что скалярное
произведение
 ,
то есть вектор
,
то есть вектор _l_
оси
_l_
оси
 ,
а пл.ll
оси
,
а пл.ll
оси

 ;
;
 ,
то есть вектор
,
то есть вектор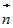 _l_
оси
_l_
оси
 ,
а пл.ll
оси
,
а пл.ll
оси
 .
. ;
;
 ,
то есть вектор
,
то есть вектор _l_
оси
_l_
оси
 ,
а пл.ll
оси
,
а пл.ll
оси
 .
. ;
в этом случае уравнение плоскости имеет
решение
;
в этом случае уравнение плоскости имеет
решение
 ,
или точка
,
или точка принадлежит
плоскости.
принадлежит
плоскости. и
и
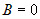 ;
пл.ll
координатным осям
;
пл.ll
координатным осям
 и
и ,
а тогда онаllкоординатной
пл.
,
а тогда онаllкоординатной
пл. .
. и
и
 ;
пл.ll
координатным осям
;
пл.ll
координатным осям
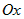 и
и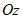 ,
а тогда онаll
координатной пл.
,
а тогда онаll
координатной пл.
 .
. и
и
 ;
пл.ll
координатным осям
;
пл.ll
координатным осям
 и
и ,
а тогда онаll
координатной пл.
,
а тогда онаll
координатной пл.
 .
. и
и
 ;
пл.ll
координатной оси
;
пл.ll
координатной оси
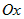 и
проходит через начало координат, то
есть проходит через координатную ось
и
проходит через начало координат, то
есть проходит через координатную ось .
. и
и
 ;
плll
координатной оси
;
плll
координатной оси
 и
проходит через начало координат, то
есть проходит через координатную ось
и
проходит через начало координат, то
есть проходит через координатную ось .
. и
и
 ;
пл.ll
координатной оси
;
пл.ll
координатной оси
 и
проходит через начало координат, то
есть проходит через координатную ось
и
проходит через начало координат, то
есть проходит через координатную ось .
.
56 острый < между пл-тями:



Усл
||  (при
этом если данное выраж. =D1/D2,
то пл-ти совпадают).
(при
этом если данное выраж. =D1/D2,
то пл-ти совпадают).

57. Прямая в пр-ве может быть задана
2
точками, точкой и напр. вектором,
кот.||прямой, пересеч. 2-х пл-тей. Различные
виды ур-ний прямой в пр-ве: 1)Ур-ние прямой,
проход через 2 задан. т-ки: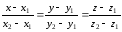 2)Канонические
ур-ния пр-мой:
2)Канонические
ур-ния пр-мой: 3)Параметр
вид канон. ур.:
3)Параметр
вид канон. ур.: 4)Общие
ур. прямой в пр-ве, т.е прямая как пересеч
2-х пл-тей:
4)Общие
ур. прямой в пр-ве, т.е прямая как пересеч
2-х пл-тей: Угол
между 2-мя прямыми:
Угол
между 2-мя прямыми:
Пр||,если

Пр
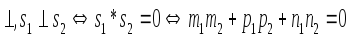
58. Усл || пр. и пл-ти:
 Усл.
Усл. Угол
между прям и пл-тью:
Угол
между прям и пл-тью:
59. Пов-тью 2-го порядка
наз пов-ть опред в Декартовой прямоуг. Системе координат ур 2-й степени относительно пер х,у,z, т.е. ур-нием вида a1x2+a2y2+a3z3+a12xy+a13xz+a23yz+b1x+b2y+b3z+c=0. Это ур. опред пов-ти след. типов:1)эллиптическая(эллипсоид, сфера) 2)гиперболическая (однополостный и двуполостный гиперболоиды, канонич. пов-ть) 3)параболическая (эллиптические и гиперболич. параболоиды) 4)цилиндрическая (эллиптический, гиперболический и парабол. Цилиндры, пара пересек или пара параллельных пл-тей).
Метод сечений состоит в том, что пов-ть рассекают пл-тями и по виду линий пересеч. Делают вывод о форме самой пл-ти. Для простоты в кач секущих пл-тей рассм координатные пл-ти и им параллельные.
60. Цилиндрической пов-тью наз
пов-ть, кот получается перемещением прямой L, наз образующей, вдоль некоторой линии k, наз направляющей, при эьом прямая перемещ. параллельно самой себе. Если напр. явл одна из линий 2-го порядка, то пов-ть наз цилиндрич пов-тью 2-го порядка.
X2/a2+y2/b2=1 – ур эллиптического цилиндра -X2/a2+y2/b2=1 – ур гипербол цилиндра x2=2py –ур парабол цилиндра
61. Понятие фнп
Если каждому набору зн-ий n-переменных величин(х1, х2,..хn)из некоторого множ. Х, по некоторому правилу F поставлено в соотв.число z из множ.Z, то говорят, что на множ.Х задана ф-я Z=f(x1,x2..xn), n-переменных со зн-ми во множ.Z. x1,x2..xn-независимые перемен. или аргументы, z-зависим.или ф-ция. Х-обл.определ.Z-обл.зн.ф-ции.D(Z)=х-любое, у-любое. Линии уровня Ф2П Z=f(x;y)-множ.точек пл-ти, в кот.ф-ция принимает одно и то же знач.(линия, ур-ние которой f(x,y)=c).
Пусть ф-ция Z=f(x;y) определена в некотор.быть может проколотой окрестн. т.M0(х0;у0).
ОПРЕДЕЛЕНИЕ.
Число А-предел ф-ции Z=f(x;y)
при х→х0, у→у0(или иначе говорят в т.М0),
если для любо й эпсилон окрестности А
сущ.такая проколот.окрестность т.М0, что
для всех отчек М(х;у) из этой проколотой
ᵟокрест.т.М0 соответ.знач.ф-ции f(x;y)
попадает в указанную эпсилон окрест.А.
Рассмотрим послед-ти
точ.М1(х1,у1),М2(х2,у2),..Мn(xn,yn)
говорят, что эта послед.сходится в
точ.М0(х0, у0)если
 .
ОПРЕДЕЛЕНИЕ.Числ
А-предел ф-ции Z=f(x;y)
в т.М0, если для любой сходящейся к М0
послед.точек М, М2, Мn,отличных
от т.М0, в сооств.поcлед.знач.
ф-ций f(M1),
f(M2)…f(Mn)
сходится к числу А. Определения 1 и 2
эквивалентны
.
ОПРЕДЕЛЕНИЕ.Числ
А-предел ф-ции Z=f(x;y)
в т.М0, если для любой сходящейся к М0
послед.точек М, М2, Мn,отличных
от т.М0, в сооств.поcлед.знач.
ф-ций f(M1),
f(M2)…f(Mn)
сходится к числу А. Определения 1 и 2
эквивалентны
62. Частной производной ф-ции Z=f(x;y), по некоторой переменной назыв.
предел
отношения частного приращения ф-ции по
этой переменной к приращению этой
переменной, если последнее .
Из определ.следует, что для нахождения
частной производной нужно продиффер.Z
по переменной х, считая, что у постоянным.
Знач. Частной производной ..
.
Из определ.следует, что для нахождения
частной производной нужно продиффер.Z
по переменной х, считая, что у постоянным.
Знач. Частной производной .. в т.(х0,у0) равно tg
угла наклона касательной проведенной
в т.ḳ(х0,у0;f(x0,y0)
к линии пересечения поверхности Z=f(x;y)
и плоскости у=у0.
(Частные
производные высших порядков. Пусть
имеется
в т.(х0,у0) равно tg
угла наклона касательной проведенной
в т.ḳ(х0,у0;f(x0,y0)
к линии пересечения поверхности Z=f(x;y)
и плоскости у=у0.
(Частные
производные высших порядков. Пусть
имеется
z=z(x;y)
↙
↘





↙ ↘ ↙ ↘ ↙ ↘ ↙ ↘
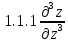
 1.2.1
1.2.1
 2.1.1
2.1.1


Теорема.
Еслі ф-ция z=z(x;y)
и ее частные произв. опреределены в нек.точке и непрерывны
в самой этой точке, то в этой точке в
рез-т диф.ФНП не зависит от порядка
диф.по различным переменным
опреределены в нек.точке и непрерывны
в самой этой точке, то в этой точке в
рез-т диф.ФНП не зависит от порядка
диф.по различным переменным
63.Ф-ция Z=f(x;y) назыв.диффер.в т. (х0,у0)
если
ее полное приращение в этой точке
представляется в виде: ,
где А, В некоторые числа, зависящие
только от т.(х0,у0) и не завис.от
,
где А, В некоторые числа, зависящие
только от т.(х0,у0) и не завис.от Необходимые
услов. Диф.Ф2П. Теорема1. Если
Z=f(x;y)
диф.в некоторой точке, то она непрерывна
в этой точке. Обратное утвержд.неверно.Теорема2.
Если
Z=f(x;y)
диф. В некоторй точке, то в этой точке
сущ.частные производные..
Необходимые
услов. Диф.Ф2П. Теорема1. Если
Z=f(x;y)
диф.в некоторой точке, то она непрерывна
в этой точке. Обратное утвержд.неверно.Теорема2.
Если
Z=f(x;y)
диф. В некоторй точке, то в этой точке
сущ.частные производные.. .
Достаточное
условие диф.Ф2П. Если
z=f(x;y)
в некоторой окрестности т.(х0, у0) имеет
частные производные непрер.в самой
точке (х0, у0), то z=f(x;y)
диф. В т. (х0,у0).
.
Достаточное
условие диф.Ф2П. Если
z=f(x;y)
в некоторой окрестности т.(х0, у0) имеет
частные производные непрер.в самой
точке (х0, у0), то z=f(x;y)
диф. В т. (х0,у0).
