32.Интегралы типа ,

где a,b,c-действительные числа, причем ,R(u,v)-рациональная функция переменных u,v.Подстановка 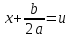позволяет выделить полный квадрат под знаком корня. В результате исходный интеграл преобразуется к одному из следующих трех типов ,которые с помощью дальнейших подстановок сводятся к интегралам от функций, рационально зависящих от тригонометрических функций.

33.«Неберущимся»

называется интеграл, который не выражается через элементарные функции, т.е. его нельзя найти. ,

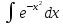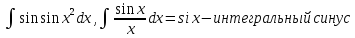
34. Комплексным числом z называется

пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:

1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;

2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида

z = (x₁ + x₂, y₁ + y₂);

3) произведением комплексных чисел z₁ и z₂ называется комплексное число

z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);

4) множество комплексных чисел , отождествляется с множеством действительных чиселR.

Разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ + z = z₁, откуда находим z = z₁ - z₂ = (x₁ - x₂, y₁ - y₂).

Частным комплексных чисел z₁ и z₂ называется комплексное число z такое, что . Отсюда находим

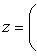
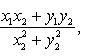
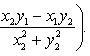
35.Матрицей размера mxn называется

прямоугольная таблица чисел(или других математических объектов)-элементов матрицы, расположенных в m строках и n столбцах.

Действия:

Сумма(разность) С=А+В(А-В) двух матриц 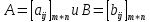,называется такая матрица элементы которой = сумме(разности)соответствующих элементов матрицы А и В.

Произведением матрицы 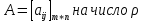называется матрица,элементы которой = соответствующим элементам матрицы А, умноженным на.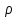

Произведение матрицы на матрицу.Нужно элементы i-той строки А умножить на соответствующие элементы j-того столбца В и полученные произведения сложить.

36. Определитель(detA)-

числ. хар-ка,которая ввод. только для квадратн.матриц . Минором э-та определителя 3-го пор. наз. опр. 2-го пор., получ. из данного опр.вычеркиванием строки и столбца, на пересеч. которых стоит данный эл-нт.Минор эл-та , стоящего на пересеч. i-й строки и j-го столбца опред., обознач. Мij. С-ва: 1.Определитель не меняет своего значения при замене всех его строк соотв. столбцами. Замечание. Опред. в правой части ф-лы называют транспонированным по отношению к определителю в левой части этой формулы.

2.Если переставить две строки (столбца) определителя, то он изменит знак. 3.опред.,содерж.нулевую стоку равен 0. 4Опред.содерж. 2 одинаковых строки равен 0 5 Общ множитель строки можно вынести за знак определителя 6 если к эл-там какой-л строки,прибавить соотв.элементы др. строки,умноженное на одно и то же число,по опред.не изменится.7.опред.можно считать по любой строке и столбцу.8.сумма произв.эл-тов какой-л строки по алгебр.заполнению эл-тов др строки,равна 0.9.сумма произв.алгебр.дополнений эл-тов некоторой строки на число в1,в2…вn равно опред.,который получ из исходного опред.с заменой этой строки на строку в1,в2…вn.10.опред.с нулями под главной диагональю равен произв. эл-тов,стоящ .на главной диагонали.11.опред.произвед.матриц равен произв.их опред.

37.Квадратная матрица называется невырожденной (неособенной),

если её определитель отличен от нуля, и вырожденной (особенной), если определитель её равен нулю.

Без доказательства примем, что

,то есть определитель произведения квадратных матриц равен произведению определителей этих матриц.

Если А – невырожденная матрица, то существует и притом единственная матрица А^-1 такая, что

.

Необходимое и достаточное условие сущ.обр.матрицы:квадратная матрица А имеет обр.матрицу тогда и только тогда,когда определитель матрицы А≠0.