
- •2.Определение предела ф-ции на языке окрестностей:
- •3.Теорема о локальной ограниченности функции, имеющей при конечный предел
- •4.Функция называется бесконечно малой
- •5.Функция называется бесконечно большой
- •8.Понятие непрерывности функции на промежутке.
- •9.Асимптотой графика функции называется
- •12. Произв сложн ф-и
- •13. Производная обратной функции равна
- •16.Теорема Ферма.Геометрический смысл теоремы Ферма.
- •17.Теорема Ролля.Геометрический смысл теоремы Роля.
- •18.Теоремы Лагранжа и Коши.Геометрический смысл теоремы Лагранжа.
- •19.Правило Лопиталя
- •20.Сравнение роста показательной,степенной и логарифмической функций.
- •22.Разложение фу-ций по фо-ле Маклорена
- •23.Определение возрастающей(убывающей)фу-ции
- •24.Отыскание точек локального экстремума фу-ции
- •25.Алгоритм нахождения наибольшего и наименьшего значений фу-ций на отрезке
- •26. Первообразной функцией для функции f(X) называется
- •28. Алгоритм интегрирования рацион.Дробей:
- •29. Универсальная тригоном подстановка
- •32.Интегралы типа ,
- •35.Матрицей размера mxn называется
- •36. Определитель(detA)-
- •38.Рангом матрицы называется
- •39.Система линейных алгебраических уравнений—
- •41.Вектором наз.
- •42.Проекция вектора на ось
- •43.Базисом на пл-сти
- •44. Направление в-ра в пространстве
- •46.Векторным произв. *называется
- •55.Исследование общего уравнения плоскости
- •57. Прямая в пр-ве может быть задана
- •60. Цилиндрической пов-тью наз
- •61. Понятие фнп
- •64.Неявно заданная фу-ция
- •65.Линии уровня.Градиент
- •66. Точка m0(x0;y0) называется точной локального максимума(минимума) функции двух переменных
- •67.Понятие об условном экстремуме.
25.Алгоритм нахождения наибольшего и наименьшего значений фу-ций на отрезке
1.Проверить,что фу-ция непрерывна на этом отрезке
2.Найти производную
3.Приравнять производную к 0,найти критические точки
4.Из критических точек выбрать те,которые лежат на отрезке
5.Найти значения фу-ций в критич.точках внутри отрезка и на концах отрезка
6.Выбрать из них наим. и наиб. значения
26. Первообразной функцией для функции f(X) называется
такая
функция F(х), производная которой равна
данной функции F’(x)=f(x).
Множество
всех первообразных некоторой
функции f(x) называется неопределенным
интегралом функции
f(x) и
обозначается как: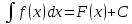 .
Основные св-ва: Производная
неопределенного интеграла равна
подынтегральной функции; дифференциал
от неопределенного интеграла равен
подынтегральному выражению, т.е.
.
Основные св-ва: Производная
неопределенного интеграла равна
подынтегральной функции; дифференциал
от неопределенного интеграла равен
подынтегральному выражению, т.е.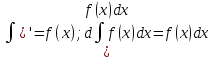 .
Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой
функции и произвольной постоянной.
Постоянный множитель можно вынести из
под знака интеграла, т.е. если k = const ≠
0.Неопределенный интеграл от алгебраической
суммы двух функций равен алгебраической
сумме интегралов от этих функций в
отдельности.Ф-ла интегрирования по
частям
.
Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой
функции и произвольной постоянной.
Постоянный множитель можно вынести из
под знака интеграла, т.е. если k = const ≠
0.Неопределенный интеграл от алгебраической
суммы двух функций равен алгебраической
сумме интегралов от этих функций в
отдельности.Ф-ла интегрирования по
частям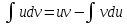 .
.
27.
Если
ф-ия f(x)непрерывна а ф-ия (t)
диференцируема и имеет непрерывную
обратную ф-ию. Пример
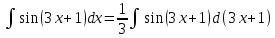 sinxdx=-d(cosx),cosxdx=d(sinx)
sinxdx=-d(cosx),cosxdx=d(sinx)
28. Алгоритм интегрирования рацион.Дробей:
Если
дробь неправильная (т.е. степень P(x) больше
степени Q(x)),
преобразовать ее в правильную, выделив
целое выражение;Разложить знаменатель Q(x) на
произведение одночленов и/или несократимых
квадратичных выражений;Разложить
рациональную дробь на простейшие дроби,
используя метод
неопределенных коэффициентов;Вычислить
интегралы от простейших дробей. Простейшие
дроби бывают 4 типов
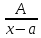 ;
;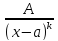 ;
;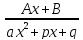 ;
; .1-ого
типа замены T=x-a. 3-его типа выделение
полного квадрата в трёхчлене и замена
t=x+
.1-ого
типа замены T=x-a. 3-его типа выделение
полного квадрата в трёхчлене и замена
t=x+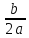
29. Универсальная тригоном подстановка
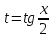 ;
;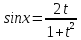 ;
;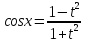 ;
;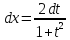 .
Подынтегральная
функция нечётна относительно sin x,
т.е. R(-sin x,
cos x)
=- R(sin x,
cos x).
В этом случае применима подстановка t =
cos x. Подынтегральная
функция нечётна относительно cos x,
т.е. R(sin x,
-cos x)
= = - R(sin x,
cos x).
В этом случае применима подстановка t =
sin x. Подынтегральная
функция чётна относительно sin x и cos x,
т.е. R(-sin x,
-cos x)
= R(sin x,
cos x). В
этом случае применима подстановка t =
tg x
.
Подынтегральная
функция нечётна относительно sin x,
т.е. R(-sin x,
cos x)
=- R(sin x,
cos x).
В этом случае применима подстановка t =
cos x. Подынтегральная
функция нечётна относительно cos x,
т.е. R(sin x,
-cos x)
= = - R(sin x,
cos x).
В этом случае применима подстановка t =
sin x. Подынтегральная
функция чётна относительно sin x и cos x,
т.е. R(-sin x,
-cos x)
= R(sin x,
cos x). В
этом случае применима подстановка t =
tg x 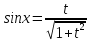 ;
;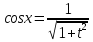 ;
;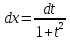
30.
Интегралы вида
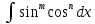 .
.
Если
ф-ия n-нечётн число, то t=sinx, если m-нечётн
число, то t=cosx, если n+m-чётное отрицательно
число то t=tgx, ф-лы понижения степени
 ,
, ,
,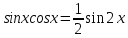
31.Пусть ![]()
–
рациональная
функция от ![]() Эта
функция, а следовательно, и интеграл от
неё, рационализируется подстановкой
x=trгде
r– наименьшее общее кратное чисел r1,
r2,…,
rn.
Тогда dx=rtr-1 и
под интегралом стоит рациональная
функция от t Аналогично, если подынтегральное
выражение
Эта
функция, а следовательно, и интеграл от
неё, рационализируется подстановкой
x=trгде
r– наименьшее общее кратное чисел r1,
r2,…,
rn.
Тогда dx=rtr-1 и
под интегралом стоит рациональная
функция от t Аналогично, если подынтегральное
выражение 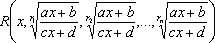 есть
рациональная функция от
есть
рациональная функция от 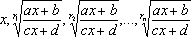 ,
то подынтегральная функция рационализируется
подстановкой
,
то подынтегральная функция рационализируется
подстановкой ![]() где
t – наименьшее общее кратное чисел r1,
r2,…,
rn.
Тогда
где
t – наименьшее общее кратное чисел r1,
r2,…,
rn.
Тогда 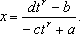 Подставляя
в исходное выражение, получаем рациональную
функцию от t .
Подставляя
в исходное выражение, получаем рациональную
функцию от t .
