
- •2.Определение предела ф-ции на языке окрестностей:
- •3.Теорема о локальной ограниченности функции, имеющей при конечный предел
- •4.Функция называется бесконечно малой
- •5.Функция называется бесконечно большой
- •8.Понятие непрерывности функции на промежутке.
- •9.Асимптотой графика функции называется
- •12. Произв сложн ф-и
- •13. Производная обратной функции равна
- •16.Теорема Ферма.Геометрический смысл теоремы Ферма.
- •17.Теорема Ролля.Геометрический смысл теоремы Роля.
- •18.Теоремы Лагранжа и Коши.Геометрический смысл теоремы Лагранжа.
- •19.Правило Лопиталя
- •20.Сравнение роста показательной,степенной и логарифмической функций.
- •22.Разложение фу-ций по фо-ле Маклорена
- •23.Определение возрастающей(убывающей)фу-ции
- •24.Отыскание точек локального экстремума фу-ции
- •25.Алгоритм нахождения наибольшего и наименьшего значений фу-ций на отрезке
- •26. Первообразной функцией для функции f(X) называется
- •28. Алгоритм интегрирования рацион.Дробей:
- •29. Универсальная тригоном подстановка
- •32.Интегралы типа ,
- •35.Матрицей размера mxn называется
- •36. Определитель(detA)-
- •38.Рангом матрицы называется
- •39.Система линейных алгебраических уравнений—
- •41.Вектором наз.
- •42.Проекция вектора на ось
- •43.Базисом на пл-сти
- •44. Направление в-ра в пространстве
- •46.Векторным произв. *называется
- •55.Исследование общего уравнения плоскости
- •57. Прямая в пр-ве может быть задана
- •60. Цилиндрической пов-тью наз
- •61. Понятие фнп
- •64.Неявно заданная фу-ция
- •65.Линии уровня.Градиент
- •66. Точка m0(x0;y0) называется точной локального максимума(минимума) функции двух переменных
- •67.Понятие об условном экстремуме.
20.Сравнение роста показательной,степенной и логарифмической функций.
при ![]()
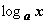 (логарифмическая
функция)=
о(
(логарифмическая
функция)=
о(![]() ),
),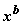 (степенная
функция)=о(
(степенная
функция)=о(![]() )
(
)
(![]() ),
т.е. при
),
т.е. при ![]() ББ
функция
ББ
функция ![]() (показательная) имеет
более высокий порядок роста, чем ББ
функции
(показательная) имеет
более высокий порядок роста, чем ББ
функции ![]() и
и 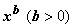 ;
ББ функция
;
ББ функция ![]() имеет
более высокий порядок роста, чем ББ
функция
имеет
более высокий порядок роста, чем ББ
функция 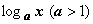
21. Фор-ла Тейлора является основой приближенных вычислений,т.к. позволяет заменить диф. Фу-цию многочленом любой степени
Фор-ла с остаточным членом в форме Логранжа:
f(x)=Pn(x)+Rn(x)
 -многочлен
Тейлора
-многочлен
Тейлора
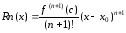 -остаточный
член в форме Логранжа
-остаточный
член в форме Логранжа
Фор-ла с остаточным членом в форме Пеано:
f(x)=Pn(x)+Rn(x)
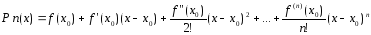 -многочлен
Тейлора
-многочлен
Тейлора
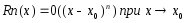 -остаточный
член в форме Пеано
-остаточный
член в форме Пеано
22.Разложение фу-ций по фо-ле Маклорена
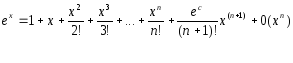
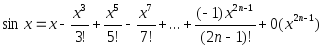
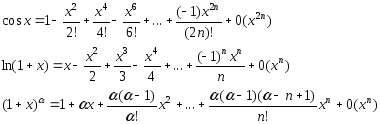
23.Определение возрастающей(убывающей)фу-ции
Фу-ция
y=f(x)назыв.возрастающей
(убывающей)на промежуткеХ,если большему
значению аргумента из этого промежутка
соответствует большее(меньшее)значение
фу-ции,то есть для x1<x2,x1и
x2 X
справедливо f(x1)<f(x2)(f(x1)>f(x2))
X
справедливо f(x1)<f(x2)(f(x1)>f(x2))
Условия монотонности диф.ф-ции на интервале:
1.пусть ф-ция f(x) диф.на интервале (а;b),тогда
1)y=f(x) назыв. неубывающей на (a;b)тогда и только тогда,когда f’(x)≥0 на (a;b)
2)y=f(x)назыв. невозрастающей на (a;b)тогда и только тогда,когда f’(x)≤0 на (a;b)
2.пусть ф-ция f(x) диф-ема на (a;b),тогда
1)если f’(x)>0 на (a;b),то y=f(x) возрастает на (a;b)
2)если f’(x)<0 на (a;b),то y=f(x) убывает на (a;b)
3.пусть ф-ция y=f(x) диф-ма на (a;b),тогда
1)y=f(x) возрастает на (a;b)тогда когда f’(x)≥0 на (a;b)причем равенство f’(x)=0 возможно только в отдельных точках этого интервала
2)y=f(x) убывает на (a;b)тогда и только тогда,когда f’(x)≤0 на (a;b)причем равенство f’(x)=0 возможно толоько в отдельных точках этого интервала
Достаточное условие выпуклости графика фц-ции
Если сущ.вторая производная f”(x) и она <0 при всех Х на (a;b),то график ф-ции f(x) является выпуклым вверх на (a;b)
Если сущ.вторая производная и она >0 при всех Х на (a;b),то график ф-ции f(x) является выпуклым вниз на (a;b)
Точки перегиба
Точка М(х0;f(x0))в уторой меняется направление выпуклости гнрафика ф-ции называется точкой перегиба
Достаточное условие перегиба:если f”(x) в некоторой точке х0 обращается в 0 или не существует и при переходе через эту точку меняет знак,то точка М(х0;f(x0))является точкой перегиба
24.Отыскание точек локального экстремума фу-ции
Точка
х0
назыв. точкой лок. max
f(x)
если для всех x x0
из некоторой окрестности т. х0
f(x0)>f(x)
x0
из некоторой окрестности т. х0
f(x0)>f(x)
Точка
х0
назыв. точкой лок. min
f(x)
если для всех x x0
из некоторой окрестности т. х0f(x0)<f(x)
x0
из некоторой окрестности т. х0f(x0)<f(x)
Необходимое условие экстремума: если х0 является точкой локального экстремума точки f(x)
То производная f’(x) в этой точке обращается в 0 или не существует(точки в которых производная обращается в 0 или не существует назыв. критическими точками или стационарными или точками возможного экстремума, но это не обяз. точки экстремума)
1 достаточный признак сущ. экстремума : пусть х0 –критическая точка непрерывной фу-ции f(x), тогда если f’(x) при переходе через точку х0 слева направо меняет знак с «-»на «+» то х0-точка лок. min;Если меняет знак с «+» на «-» то х0-точко лок. max
2 достаточный признак сущ.экстремума:пусть х0-критич.точка f(x) и ф-ция дважды диф-емы в окрестности х0,тогда, если f”(x0)<0,то х0-т.лок.max;если f”(x0)>0,тох0-т.лок. min;если f”(x0)=0,то х0-может являться точкой лок.экстремума,а можети не являться точкой лок.экстремума
3
достаточный признак сущ.экстремума:пусть
х0-критич.точка
f(x)
и ф-ция f(x)
n-раз
диф-ма в окрестности т.х0
причем f’(x0)=f”(x0)=…=fn-1(x0)=0
f(n)(x0) 0
тогда
0
тогда
1)если n-четное число и f(n)(x0)<0,то х0-точка лок.max
2)если n-четное и f(n)(x0)>0,то х0-точка лок.min
3)если n-нечетное,то х0-не является точкой лок.экстремума
Алгоритм нахождения точек локального экстремума
