
С.А. Парыгина и др Математика -Часть 3
.pdf
Задание 13. Найдите объем тела, образованный вращением фигуры, ограниченной графиками функций.
|
x |
|
1 |
|
13.2. y 2x x2 , y x 2 , во- |
|
13.1. y 2 |
|
, y 4 , вокруг оси ОХ |
круг оси ОХ |
|
||
13.3. y x3, y x2 , вокруг оси ОУ |
13.4. y (x 1)2 , x 0, x 2, y 0 , |
|||||
|
|
|
|
|
вокруг оси ОУ |
|
|
|
|||||
13.5. y x 2 3x 2, y 0 , вокруг |
13.6. y 2x x2 , y 0 , вокруг оси |
|||||
оси ОУ |
|
|
|
|
ОХ |
|
|
|
|
||||
13.7. y x2 |
1, y x, x 0, x 1, |
13.8. y x 8, y x, x 0, вокруг |
||||
вокруг оси ОУ |
|
|
оси ОУ |
|
||
|
|
|
||||
13.9. y x2 , y2 |
x, вокруг оси ОХ |
13.10. y x3, y x, вокруг оси |
||||
|
|
|
|
|
ОХ |
|
|
|
|
||||
13.11. y 3 x2 , y x2 1, вокруг |
13.12. y x2 |
1, y 3x 1, вокруг |
||||
оси ОХ |
|
|
|
|
оси ОХ |
|
|
|
|
||||
13.13. y2 4x, |
x 4 , вокруг оси |
13.14. y 2x x2 , y 4x 2x2 , во- |
||||
ОУ |
|
|
|
|
круг оси ОХ |
|
|
|
|
|
|||
13.15. y x2 , x 2, y 0, |
вокруг |
13.16. y x2 |
2x 1, x 2, во- |
|||
оси ОУ |
|
|
|
|
круг оси ОУ |
|
|
|
|
||||
13.17. y x2 5x 6, y 0, во- |
13.18. y x3 |
2, y 1, вокруг |
||||
круг оси ОХ |
|
|
|
|
оси ОХ |
|
|
|
|
||||
13.19. y 1 x2 , x 0, x |
y 2, |
13.20. y x3, y 8, x 0, вокруг |
||||
вокруг оси ОХ |
|
|
оси ОУ |
|
||
|
|
|||||
13.21. y (x 2)2 , y 0, x 0 , во- |
13.22. y x2 , y 1, x 2 ,вокруг оси |
|||||
круг оси ОУ |
|
|
|
|
ОХ |
|
|
|
|||||
13.23. y x2 2, y 0, x 1, во- |
13.24. y x2 , y x, вокруг оси |
|||||
круг оси ОХ |
|
|
|
|
ОУ |
|
|
|
|||||
13.25. y (x 2)2 , y 0, x 0, во- |
13.26. y x2 8x 7, y 0, во- |
|||||
круг оси ОУ |
|
|
|
|
круг оси ОХ |
|
|
|
|
|
|
|
|
71
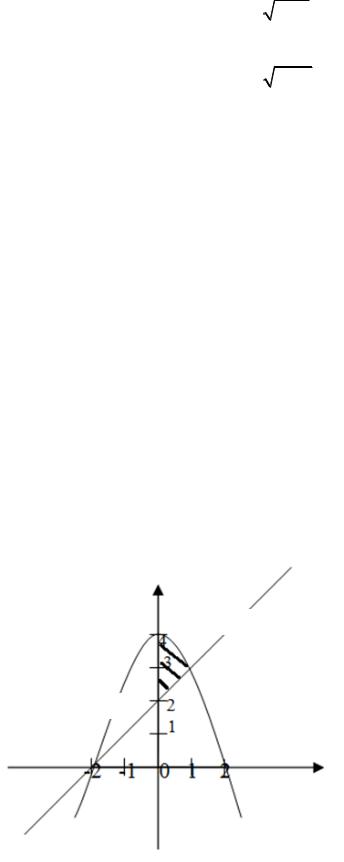
13.27. y x2 |
8x 7, y 0, во- |
13.28. y |
x 1, x 5, y 0, во- |
круг сои ОХ |
|
круг оси ОУ |
|
|
|
|
|
13.29. y x2 |
2, y 1, вокруг |
13.30. y |
2 x, y 0, x 2, во- |
оси ОУ |
|
круг оси ОХ и ОУ |
|
|
|
|
|
Образец выполнения задания 13
Найдите объем тела, образованный вращением фигуры, ограниченной графиками функций:
y 4 x2 , y 2 x, x 0 , вокруг оси ох и оси оу.
Р е ш е н и е .
1) Найдите объем тела, образованного вращением фигуры, ограниченной графиком функций вокруг оси ох.
Найдем координаты точек пересечения графиков функций
y 4 x2 , y 2 x , |
4 x2 2 x, x2 x 2 0, x 1, x |
2 |
2, т.к. |
|
1 |
|
x 0, то х1 = 1, следовательно у1 = 2 + 1 = 3.
Координаты точки пересечения А(1; 3). Построим графики функций у = 4 - х2, у = 2 + х.
у
у = 2 + х
у = 4 – х2
х
72

Для нахождения объема воспользуемся формулой:
b
V f 2 (x) dx
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
V = V1 – V2 , где V1 – объем |
образованный вращением у = 4 - х2, |
|||||||||||||||
x |
|
|
вокруг |
оси ОХ, V |
2 |
– объем |
образованный |
вращением |
||||||||
|
0;1 |
|
||||||||||||||
y |
2 x, x |
|
|
|
вокруг оси ОХ. |
|
|
|
|
|
||||||
|
0;1 |
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
V (4 x2 )2 dx (2 x)2 dx ((4 x2 )2 (2 x)2 )dx |
||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
5 |
|
12x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
(x4 |
12x2 |
12)dx |
x |
|
|
12х |
1 |
1 4 12 |
8 1 ед3. |
|||||||
|
|
|
||||||||||||||
|
|
0 |
|
|
|
|
5 |
|
3 |
|
|
0 |
5 |
5 |
||
|
|
|
|
|
|
|
|
|
||||||||
О т в е т : 8 15 ед3.
2)Найдем объем тела вращения, образованного вращением фигуры, ограниченной графиками функций вокруг оси ОУ.
y 4 x2 , x2 4 y, x 4 y, т.к. x 0 , |
x 4 y . |
y 2 x x y 2.
Для нахождения объема воспользуемся формулой:
d
V x2 ( y)dy.
|
|
|
c |
|
V = V1 + V2 , где V1 – объем образованный вращением x |
4 y |
|||
y 3; 4 вокруг |
оси ОУ, V2 – объем образованный вращением |
|||
x y 24, y |
|
|
|
|
|
2;3 вокруг оси ОУ. |
|
||
73

|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V V1 V2 |
|
4 y 2 dy ( y 2) 2dy |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
4 |
|
|
|
|
y |
3 |
|
|
4 y |
2 |
|
|
3 |
|||
(4 y)dy ( y 2)2 dy |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
4 y |
|
|
|
|
|
|
|
|
|
4 y |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
3 |
|
|
|
2 |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
16 |
|
|
|
|
9 |
|
|
|
|
27 |
2 9 |
12 |
|
|
|
|
8 |
2 4 |
4 2 |
|
|
||||||||||||||
16 |
2 |
|
12 |
|
|
|
|
3 |
|
|
|
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
8 |
15 |
|
|
|
3 |
8 |
|
|
1 |
|
1 |
|
|
5 |
ед3. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
3 |
|
2 |
3 |
|
6 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
О т в е т : |
5 |
ед3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 14. Найдите несобственные интегралы или доказать их расходимость.
14.1. |
|
|
|
|
|
|
|
|
|
|
|
|
14.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
|
3 |
|
x4 |
dx ; |
|
1) |
|
2x dx |
|
; |
|
|
|
||||||||||||||||||
|
|
x |
e |
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
dx |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|||
2) |
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3x 6 |
|
|
|
|
(3 x) |
3 |
|
|||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14.3. |
|
|
|
|
|
|
|
|
|
|
|
|
14.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
; |
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
dx ; |
|||||
|
|
25 4x |
2 |
|
|
|
|
|
4 |
|
1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||
|
5 |
|
|
|
|
x dx |
|
|
|
|
|
5 |
|
x dx |
|
|
|
|
|
|
|
|
||||||||||
2) |
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
25 x2 |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
14.5. |
|
|
|
|
|
|
|
|
|
|
|
|
14.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||
1) |
|
|
|
|
|
|
|
|
|
; |
1) |
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||
|
x |
2 |
8x 25 |
|
|
|
|
|
2 |
|
|
x |
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
xln |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
dx |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
dx |
|
|
|
|||||||
2) |
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
xln |
3 |
x |
|
|
|
|
x |
2 |
|
4x 3 |
||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74
14.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
ln x dx ; |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
1) |
|
|
|
|
1) |
|
|
|
|
dx ; |
|
|
|||||||||||||||||||||||||
|
|
|
|
6 |
|
|
|||||||||||||||||||||||||||||||
|
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||||
2) |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x2 |
9 |
|
|
|
|
|
x2 25 |
|
|
||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||||
14.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ln3 x dx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1) |
|
|
|
|
1) |
x2e x3 dx ; |
|
|
|||||||||||||||||||||||||||||
|
e |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
3 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
5 (x 1)4 |
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
14.11. |
|
|
|
|
|
|
|
|
|
|
|
14.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
2x dx |
|
|
|||||||||||||
1) |
e x |
dx ; |
|
|
1) |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
e |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
xln x |
|
|
|
|
|
|
|
|
3 (4 x)2 |
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||
14.13. |
|
|
|
|
|
|
|
|
|
|
|
14.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
2x |
2dx |
|
|
|
|
|
|
|||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
1) |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
; |
|
|
|
|
||
|
|
|
x |
2 |
6x |
11 |
|
|
|
x |
1 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
11 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
3 |
|
|
|
x 3 |
|
|
|
|
|
|
|||||||||||||
14.15. |
|
|
|
|
|
|
|
|
|
|
|
14.16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
dx |
|
|
|||||||||||
1) |
|
|
|
|
; |
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
x |
2 |
6x |
10 |
|||||||||||||||||||||||||
|
|
|
5 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
1 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
(2 x) |
5 |
|
|
|
|
|
xln x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
14.17. |
|
|
|
|
|
|
|
|
|
|
|
14.18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 dx |
|
|
|
|
|
|
|
|||||||||
1) |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
10 |
|
4 |
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 x2 |
|
|
|
|
|
|
(7 x) |
4 |
|
|
|
|
||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||
75

14.19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
14.20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||||
|
|
3 |
e |
dx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1) |
|
x |
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
2 |
8x |
|
20 |
||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
xdx |
|
|
|
|
|
|
|
|
|
||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 x |
2 |
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
||||||||||||||
14.21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
14.22. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 x |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||||||
1) |
|
|
|
|
|
dx ; |
|
|
1) |
0 |
|
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(1 2x)2 |
|
|
|||||||||||||||||||||||||||||
x2 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
4 |
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
3x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14.23. |
|
|
|
|
|
|
|
|
|
|
|
|
|
14.24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
; |
1) |
|
|
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||
|
|
x |
2 |
8x |
17 |
|
|
(1 x)2 |
|
|
|||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||
2) 2 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
2) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
9 x2 |
|
|
|
(2x 3)4 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
14.25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
14.26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||||
|
x ln |
3 |
x |
|
|
|
|
|
(1 x) |
|
x |
|
|
|
|||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
5 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
1 x4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
|
|
|
5 x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
14.27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
14.28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||
1) |
xe x2 dx ; |
|
|
|
1) |
|
|
|
|
|
; |
|
|
||||||||||||||||||||||||||||
|
|
|
|
25 9x |
2 |
|
|
||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
6 |
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
e |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
5 |
|
|
|
|
x 6 |
|
|
|
|
|
|
|
|
1 хln |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
14.29. |
|
|
|
|
|
|
|
|
|
|
|
|
|
14.30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||||||
1) |
|
|
|
|
|
|
|
|
; |
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||||
|
|
x |
2 |
2x |
5 |
|
|
x |
2 |
2x 5 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
4 |
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x 3 |
|
|
|
|
|
|
|
|
4 |
x 2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76

Образец выполнения задания 14
Найдите несобственные интегралы или доказать их расходимость:
1) x dx ;
x4 9
6dx
2)2 x x 2 .
Р е ш е н и е .
|
|
xdx |
|
|
|
1 |
|
|
|
dx2 |
1 |
|
1 |
|
|
x2 |
|
|
|
1 |
|
|
( )2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
(arctg |
|
|
||||
|
4 |
|
|
2 |
|
2 |
|
2 |
2 |
2 |
3 |
3 |
|
6 |
3 |
||||||||||||||||
|
x |
|
9 |
|
|
|
(x |
|
) |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
arctg |
( )2 |
|
1 |
(arctg( ) arctg( )) |
1 |
|
|
|
|
0, |
интеграл |
||||||||||||||||||||
3 |
|
) |
6 |
6 |
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
сходится.
О т в е т : 0, интеграл сходится.
2)
6 |
|
|
|
|
y |
|
1 |
|
, x 2 2;6 , |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
dx |
|
x |
x 2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x 2 |
точка разрыва второго рода. |
|
|||||||||||||||||||
x |
|
x 2 |
|||||||||||||||||||||
|
|
введемзамену: |
x 2 |
t, x 2 t2 , x t2 |
2, dx 2tdt |
|
|||||||||||||||||
|
|
|
|
|
приx |
2,t |
0,приx 6,t 2 |
|
|
|
|||||||||||||
2 |
|
2tdt |
|
2 |
|
|
dt |
|
|
|
1 |
|
|
t |
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
arctg |
|
|
|
|
0 |
|
2(arctg 2 |
arctg0) |
|||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
0 |
(t |
|
2)t |
|
0 t |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2(arctg |
2 0) |
|
2arctg |
2 , интеграл сходится. |
|
|
|||||||||||||||
|
О т в е т : |
2arctg |
2 ,интеграл сходится. |
|
|
||||||||||||||||||
77
Литература
1.Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 2003.
2.Берман Г.Н. Сборник задач по курсу математического анализа: учебное пособие.- 22 изд., перераб. – СПб.: Профессия, 2003 – 2006.
3.Баврин И.И., Матросов В.Л. Высшая математика: учебник для вузов. –
М.: ВЛАДОС, 2004. – 399 с.
4.Данко П.Е., Попов А.Г., Кожевникова Т.А. Высшая математика в уп-
ражнениях и задачах: в 2 ч. – 6-е изд. – М.: ОНИКС, 21 век. Мир и образова-
ние, 2002. – Ч. 1.
5.Кузнецов Л.А. Сборник заданий по высшей математике (типовые расче-
ты). – М.: Высш. шк., 1994.
6.Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для втузов. – М., 2004.
7.Сборник задач по математике для втузов / Под ред. А.В. Ефимова. –
М.: Наука, 2004. – Ч. 1 – 3.
8.Пискунов Н.С. Дифференциальное и интегральное исчисления. – М.:
Наука, 1985.
78

Оглавление |
|
Введение .......................................................................................................... |
3 |
Введение в математический анализ .............................................................. |
4 |
Дифференциальное исчисление функции одной переменной .................. |
21 |
Интегральное исчисление функции одной переменной............................. |
40 |
Литература ...................................................................................................... |
78 |
Печатается в авторской редакции Технический редактор М.Н. Авдюхова Лицензия А № 165724 от 11.04.06 г.
Подписано в печать 27.07.12 г. Формат 60 84 1/16 . Гарнитура таймс. Уч.-изд. л. 4. Усл. п.л. 4,5.
Тир. 4. Зак.
ФГБОУ ВПО «Череповецкий государственный университет» 162600 г. Череповец, пр. Луначарского, 5.
79
