2.2 Ортогональная система трех плоскостей проекций

В практике для изображения геометрических объектов, решения некоторых задач возникает необходимость использовать третью плоскость проекций ₃, перпендикулярную₁и₂.₃–профильная плоскостьпроекций.А₃– профильная проекция точкиА.

Система трех плоскостей проекций делит пространство на 8 октантов, которые условно обозначают согласно рис. 2.3.

Р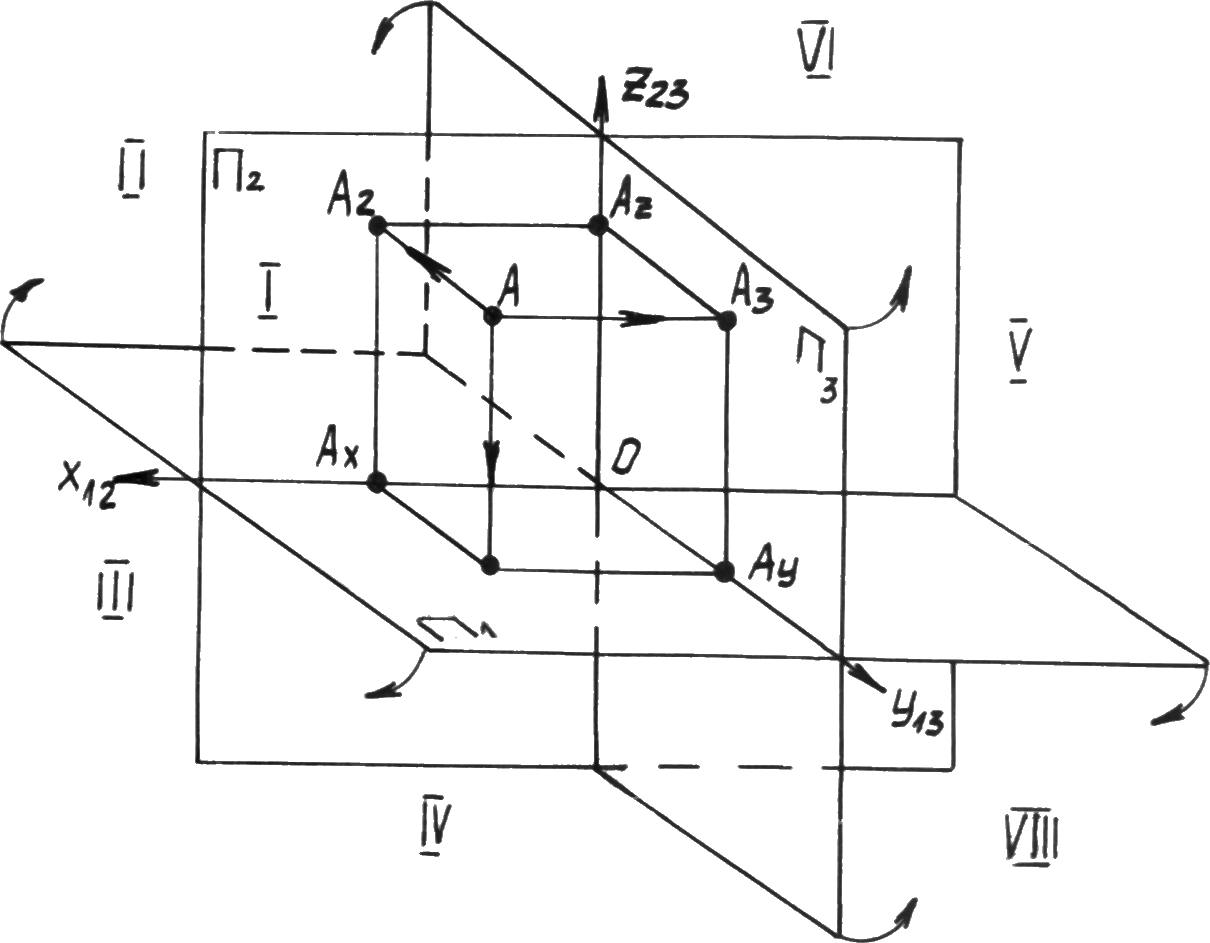ис. 2.3. Система 3^хплоскостей проекций.

В первом октанте все координаты положительные.

Чтобы перейти к чертежу на плоскости, совместим все три плоскости в одну плоскость ₂по направлениям,указаннымна чертеже. Плоскость₁вращаем вокруг осиx₁₂на 90, плоскость₃– вокруг осиz₂₃на 90против часовой стрелки. При этом осьyраздваивается.

Получается комплексный чертеж точки (рис. 2.4).

Р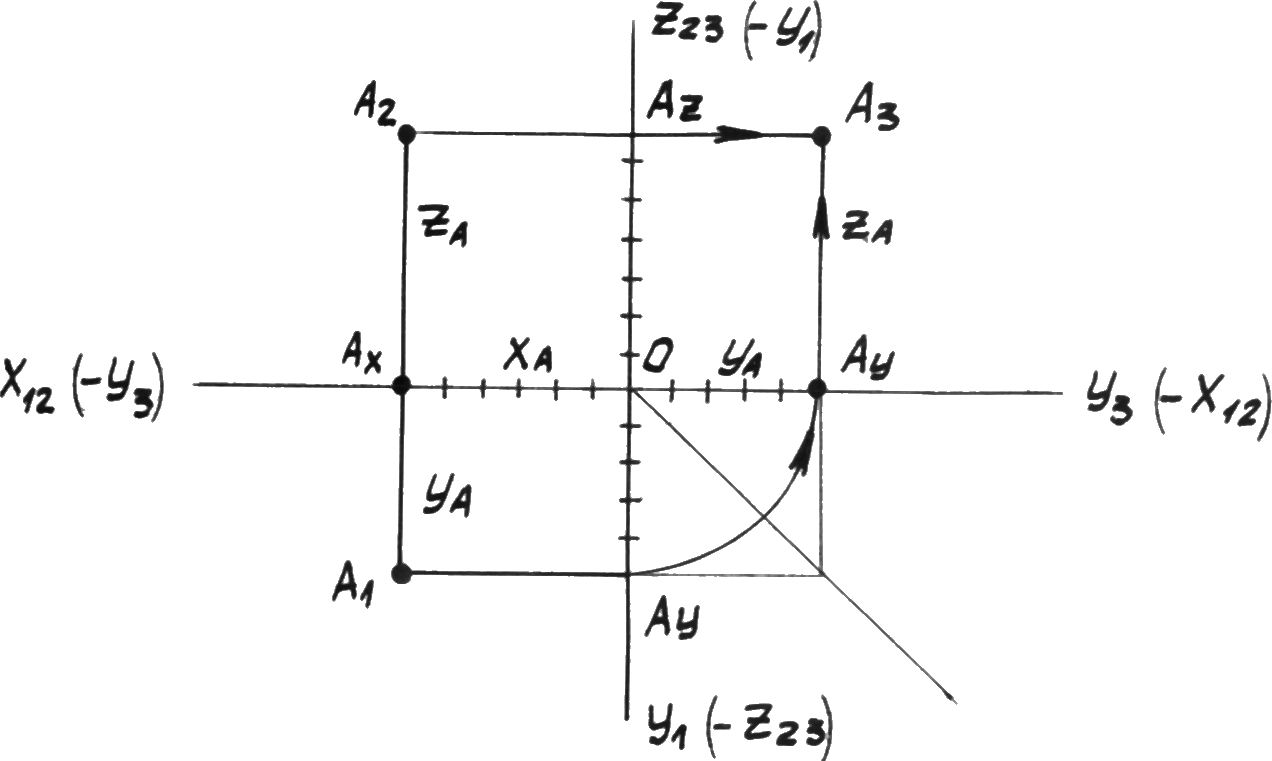ис. 2.4. Комплексный чертеж.

На комплексном чертеже все проекции точки А₁,А₂,А₃находятся в проекционной связи. Каждая проекция точки определяется двумя координатами:

А₁–x,y₁

А₂–x,z

A₃–y₃,z

В данном примере x= 30,y= 25,z= 35. Третья профильная проекция точки может быть определена по линиям связи от проекцийА₁иА₂. ПроекцииА₂иА₃расположены на одной горизонтальной линии связи, которая определяется координатойz(отрезокOA_z), а от горизонтальной проекцииА₁проводим линию связи перпендикулярно осиy₁, отрезокOA_y(координатаy) переносим против часовой стрелки на горизонтальную осьy₃и восставляем перпендикуляр (линию связи) до пересечения с горизонтальной линией связи отА₂. Координатау отА₁переносится на горизонтальную осьу₃всегда против часовой стрелки, т.к. плоскость₃при совмещении с₂разворачивается против часовой стрелки.

Профильную проекцию А₃можно определить, откладывая координаты на соответствующих осях проекций с учетом знака.

Знаки координат зависят от того, в каком октанте расположена точка.

Координаты	Октанты
	I	II	III	IV	V	VI	VII	VIII
x	+	+	+	+	-	-	-	-
y	+	-	-	+	+	-	-	+
z	+	+	-	-	+	+	-	-

2.3 Точки разных углов пространства. Точки частного положения

Если точка не принадлежит ни одной плоскости проекций, она занимает общееположение.

Если точка расположена в плоскости проекций или на оси проекций, она занимает частноеположение.

Рассмотрим ряд точек общего положения (рис. 2.5, 2.6).

Точка В(x= 30,y= 25,z= -35) –IVоктант. ПроекцияВ₁расположена ниже осиxна положительном направлении осиу. ТраекторияВ₂расположена тоже ниже осихна отрицательном направлении осиz.В₃определяется по линиям связи отВ₁иВ₂или по координатамy= 25,z= -35.

Точка С(x= -30,y= 40,z= 30) –Vоктант. ПроекцияС₁расположена справа от осиzна отрицательном направлении осиxи ниже осихна положительном направлении осиу. ПроекцияВ₂расположена выше осихна положительном направлении оси

Р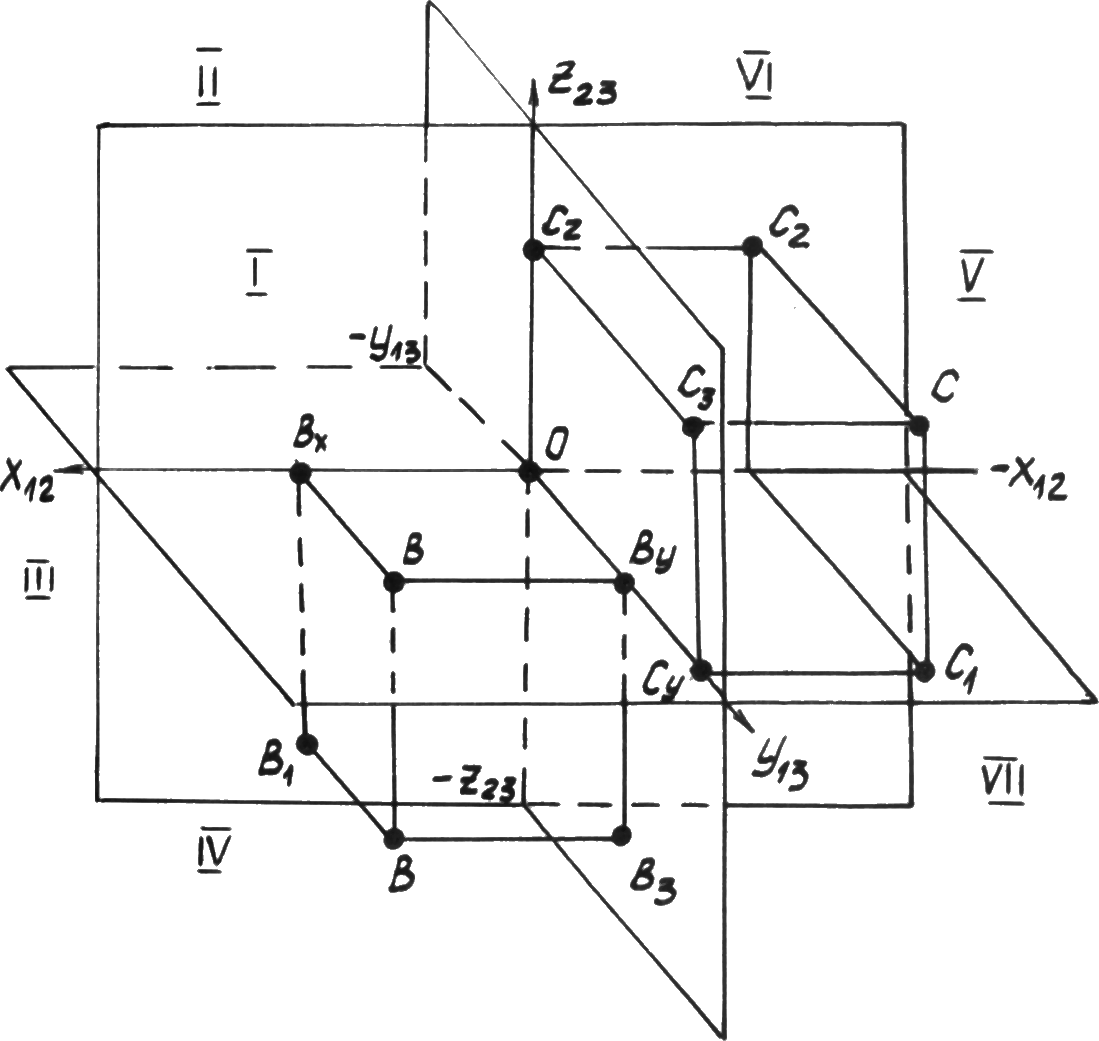ис. 2.5. Точки в 4 и 5 октанте.

Р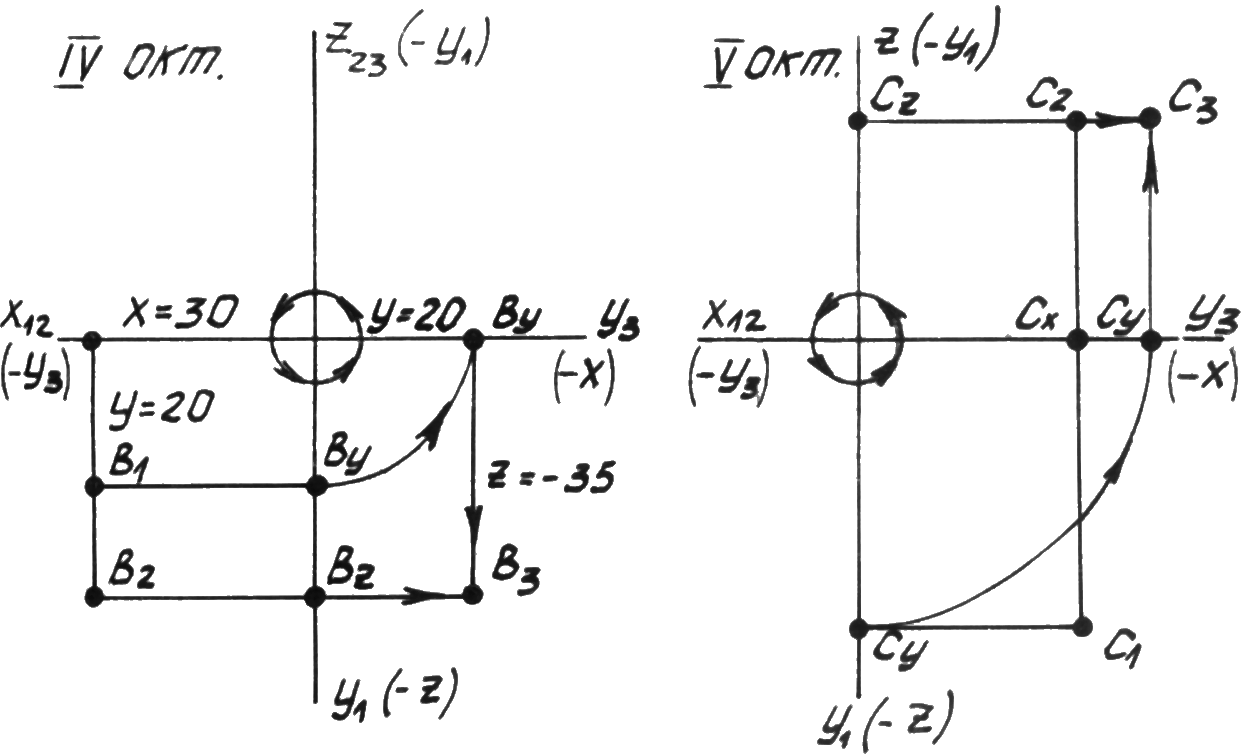ис. 2.6. Комплексный чертеж точек в 4 и 5 октантах.

z.С₃определяется по линиям связи отС₁иС₂или по координатамy= 40,z= 30.

Рассмотрим точки частного положения, расположенные на плоскостях и осях проекций.

Если координата х= 0, то точка принадлежит плоскости₃.

Если координата у= 0, то точка принадлежит плоскости₂.

Если координата z= 0, то точка принадлежит плоскости₁.

Рассмотрим ряд точек частного положения (рис. 2.7, 2.8).

Рис. 2.7. Точки частного положения.

Точка D(x= 0,y= 30,z= 20) принадлежит плоскости₃и совпадает с профильной проекциейD₃, проекцииD₁иD₂расположены соответственно на осяхуиz.

Точка Е(x= 30,y= 0,z= 35) принадлежит плоскости₂и совпадает с фронтальной проекциейЕ₂, проекцииЕ₁иЕ₃расположены соответственно на осяхxиz.

Точка К(x= 40,y= 25,z= 0) принадлежит плоскости₁и совпадает с горизонтальной проекциейК₁, проекцииК₂иК₃расположены соответственно на осяхxиу.

Точка L(x= 0,y= 5,z= 40) расположена на осиz.

Рис. 2.8. Комплексный чертеж точек частного положения.