4.5.4.Пересечение прямой линии с плоскостью .

Рассмотрим общий случай пересечения прямой с плоскостью, когда и плоскость и прямая общего положения.

На рис. 4.16. дана плоскость треугольник АВСи прямаяl.

Определить точку пересечения К. Алгоритм решения задачи:

1. Прямую lзаключаем вспомогательную проецирующую плоскость, в нашем случае, горизонтально проецирующую  ₁l₁  ₁.

2. Строим линию пересечения данной плоскости и вспомогательной (АВС)(12).

3. Определяем искомую точку на пересечение линии пересечения и проекции прямой l(1₂2₂)  l₂  K₂  K₁.

4. Определяем видимость прямой lотносительно точки пересечения.

Т.к. стороны треугольника АВСи прямойlявляются скрещивающимися прямыми, видимость определяем по конкурирующим точкам.

Если в задаче на определение точки встречи прямой линии с плоскостью один из геометрических объектов – частного положения, то в ведение вспомогательной плоскости не требуется. Рассмотрим эти случаи.

Р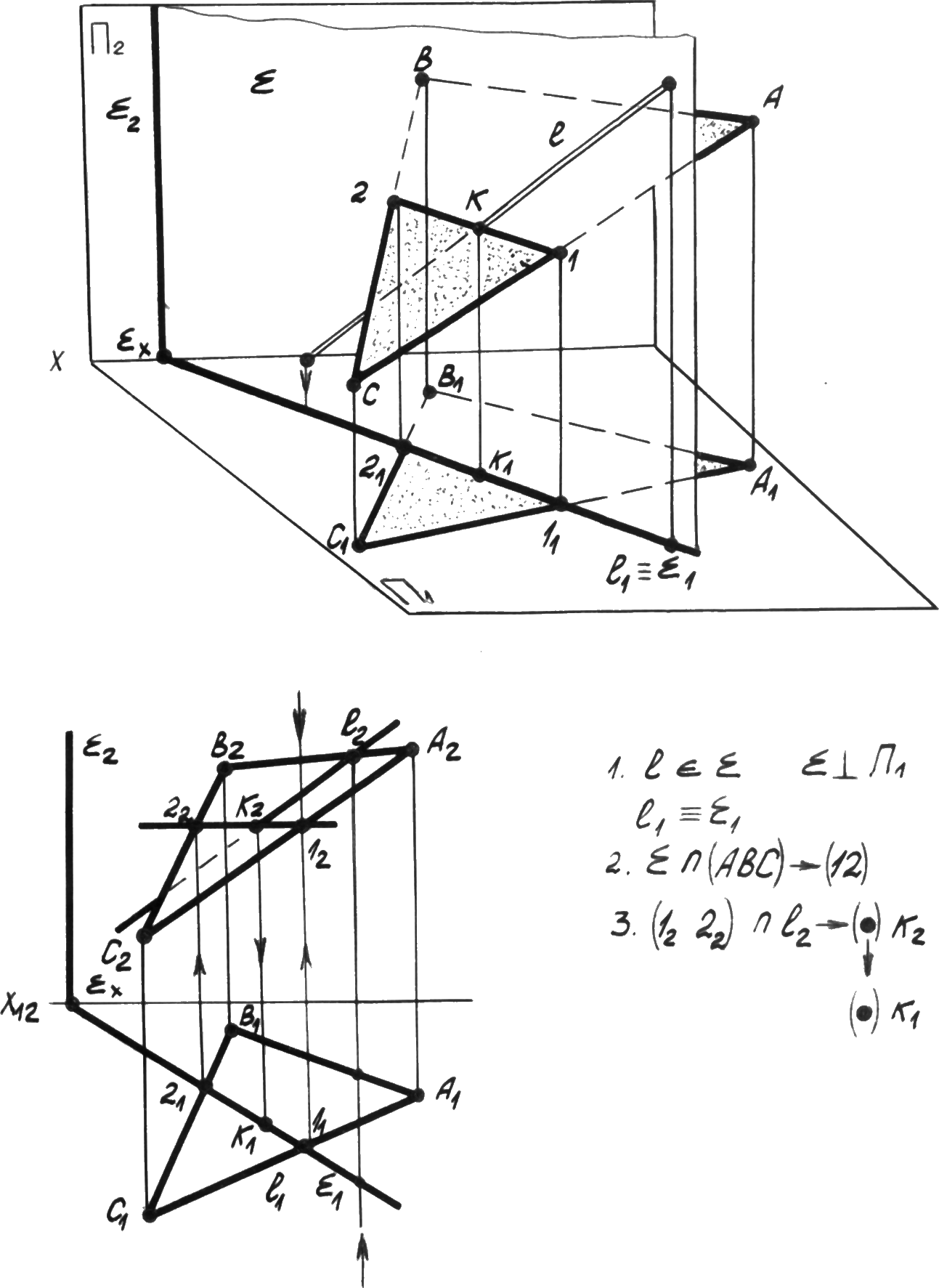ис. 4.16. Пересечение прямой линии с плоскостью.

Задача:Дана плоскость (СDЕ) – горизонтально проецирующая и прямая линияlобщего положения (рис. 4.17а) Определить точку их пересечения.

Р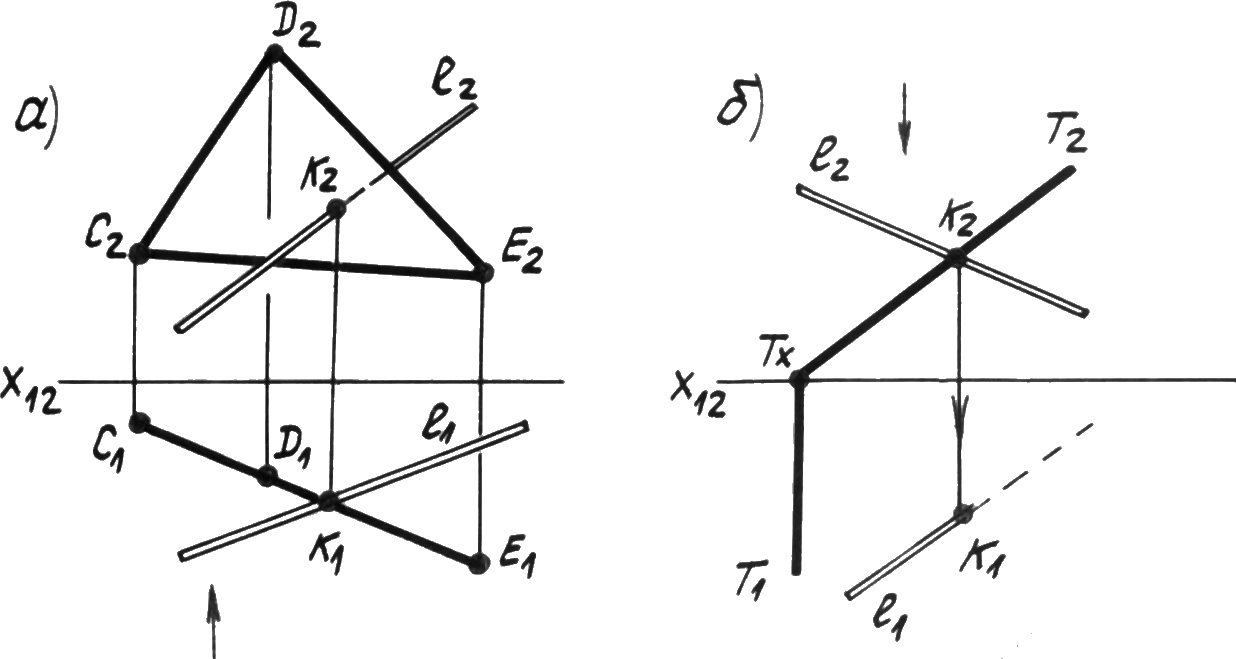ис. 4.17.

Решение:Так как треугольникCDE– горизонтально проецирующая плоскость и проецируется на₁в прямую линию, то пересечение прямойlопределяем на пересечении горизонтальных проекций объектов в единственной точкеК₁. Далее определяем видимость прямойlотносительно точки пересеченияК.

Аналогично решаем задачу на рис. 4.17б, где плоскость Т задана следами и является фронтально проецирующей.

Задача:Дана плоскость (AВC) – общего положения и фронтально проецирующая прямаяl.Определить точку их пересечения (рис. 4.18а).

Решение:Так как прямаяlявляется фронтально проецирующей и проецируется на плоскость₂в точку, то фронтальная проекция точки пересеченияК₂совпадает сl₂. Горизонтальную проекцию точки пересеченияК₁определяем из условия принадлежности точкиКи прямойlплоскостиАВС.Проводим вспомогательную прямую (12), принадлежащую плоскости, черезК₂. Рассматриваем видимость прямойlотносительно точки пересеченияК. Аналогично решаем задачу на рис. 4.18б, где плоскость Г задана следами, а прямаяlперпендикулярна плоскости₁.

р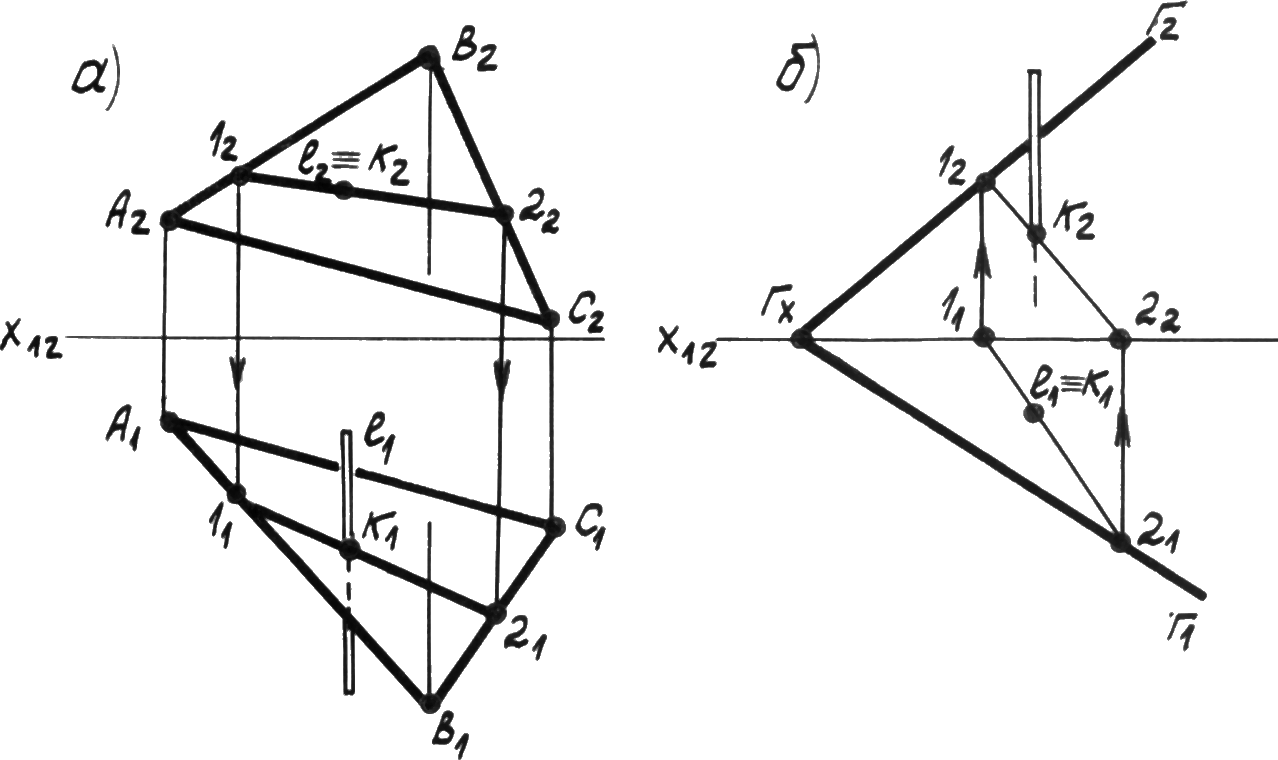ис. 4.18.

4.5.5. Прямая линия, перпендикулярная плоскости.

Прямая линия перпендикулярна плоскости, если она перпендикулярна любым двум пересекающимся прямым плоскости.

Однако распознать перпендикулярность прямой линии и плоскости в общем случае сложно, т.к. прямой угол проецируется на плоскость проекции в натуральную величину, когда одна из его сторон параллельна данной плоскости проекций. Следовательно, если на некоторой плоскости (рис. 4.19) провести две пересекающиеся прямые, одна из которых горизонтальh||, а другая - фронтальf||₂, то перпендикулярная к плоскостипрямаяaпроецируется на плоскость₁перпендикулярноh₁, а плоскость₂перпендикулярнаf₂.

Р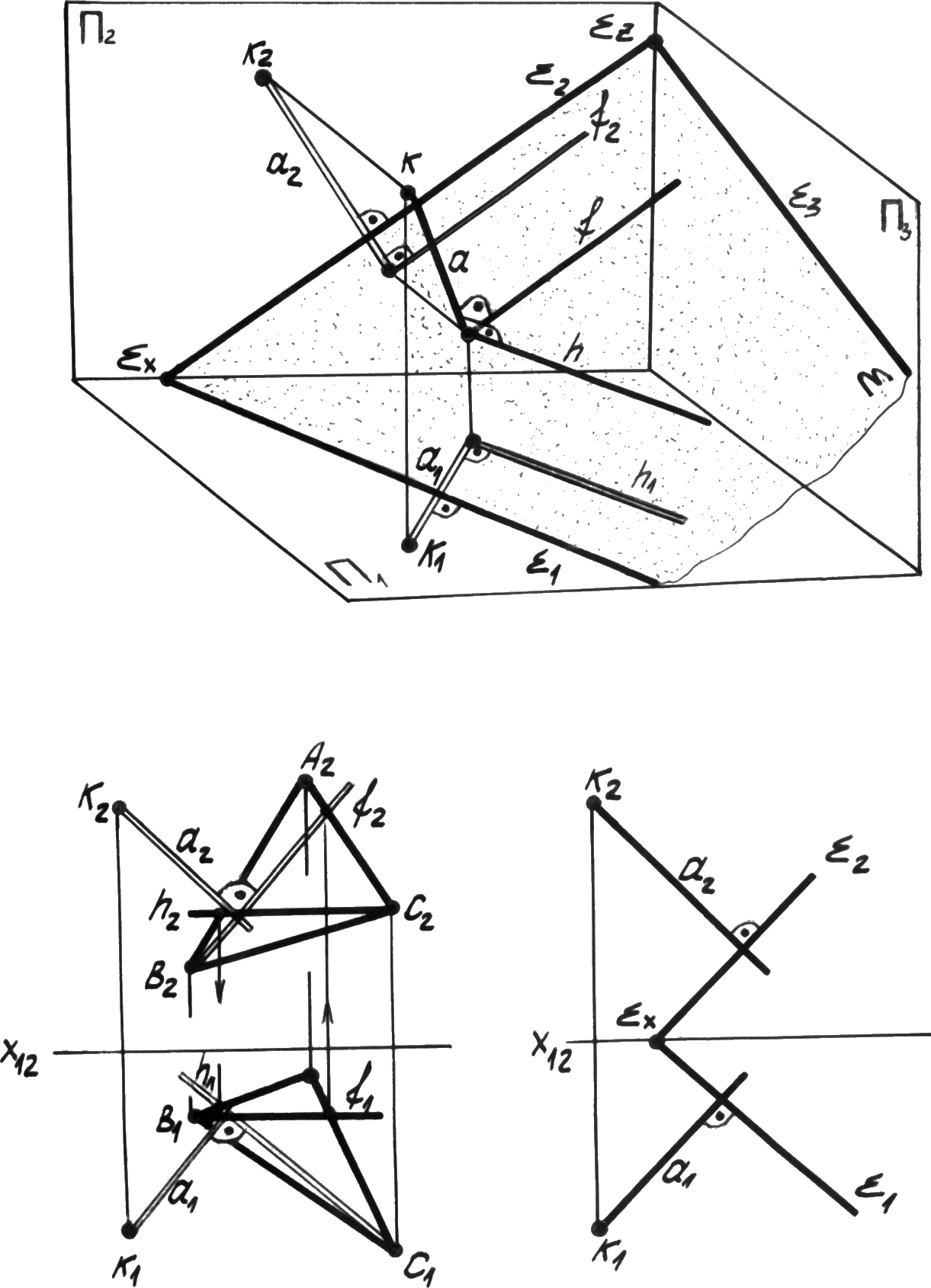ис. 4.19. Прямая линия, перпендикулярная плоскости.

Итак: если прямая линия перпендикулярна к плоскости, то её горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали, а её фронтальная проекция – перпендикулярна фронтальной проекции фронтали, а также к одноимённым следам.

На рис. 4.19 рассмотрены случаи построения перпендикуляра из точки Kк треугольникуАВСи к плоскости, заданной следами. Если плоскости заданы не следами, то первоначально всегда требуется определить горизонталь и фронталь в плоскости.