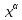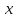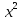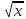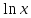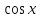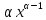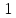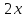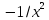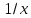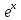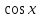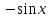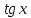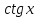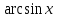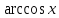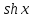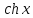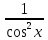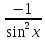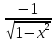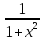MATEMATIKA_EKZAMEN / ЛЕКЦИИ2 / Тема 5 Производная
.docxТема 5 Производная
Задача
о мгновенной скорости. Рассмотрим
материальное тело движущееся по оси
Ох. Предположим, что нам известен закон
движения – функция
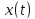 ,
задающая координату точки в момент
времени
,
задающая координату точки в момент
времени
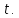 Фиксируем какой-либо момент времени
Фиксируем какой-либо момент времени
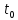 .
Поставим задачу об определении и
вычислении мгновенной скорости
.
Поставим задачу об определении и
вычислении мгновенной скорости
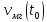 в момент времени
в момент времени
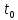 .
Придадим приращение
.
Придадим приращение
 времени и найдем соответствующее ему
приращение координаты
времени и найдем соответствующее ему
приращение координаты
 . Тогда отношение приращения координаты
к приращению времени задает среднюю
скорость на временном участке
. Тогда отношение приращения координаты
к приращению времени задает среднюю
скорость на временном участке
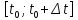 :
:
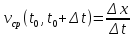 (1)
(1)
Мгновенную
скорость определим как предел средней
скорости при
 :
:
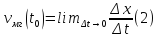
Пример.
Закон падения тела с высоты без учета
сопротивления воздуха задается как
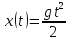 (
( -- ускорение свободного падения). Вычислим
скорость тела после 3-х секунд падения:
-- ускорение свободного падения). Вычислим
скорость тела после 3-х секунд падения:
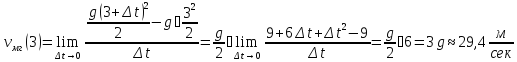
Задача о касательной. Пусть на
плоскости или в пространстве задана
некоторая кривая γ и точка P на ней.
Требуется определить понятие касательной
к γ в точке P. Выберем точку
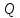 на кривой
на кривой
 ,
не совпадающую с точкой
,
не совпадающую с точкой
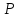 .
Проведем через точки
.
Проведем через точки
 и
и
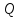 прямую
прямую
 ,
называемую секущей. Касательной в точке
P к кривой γ назовем предельное положение
секущих
,
называемую секущей. Касательной в точке
P к кривой γ назовем предельное положение
секущих
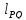 ,
в случае, когда точка Q приближается к
точке P, оставаясь на кривой γ. Пусть
теперь γ -- график функции
,
в случае, когда точка Q приближается к
точке P, оставаясь на кривой γ. Пусть
теперь γ -- график функции
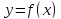 ,
и точка P имеет координаты
,
и точка P имеет координаты
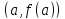 .
Рассмотрим точку
.
Рассмотрим точку
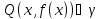 . Обозначим
. Обозначим
 и назовем эти величины приращением
аргумента и приращением функции
соответственно. Тогда угловой коэффициент
секущей
и назовем эти величины приращением
аргумента и приращением функции
соответственно. Тогда угловой коэффициент
секущей
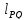 будет равен
будет равен
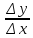 и ее уравнение будет
и ее уравнение будет
Рис. 1 Касательная

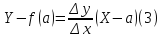
Если
 ,
то
,
то
 ,
причем
,
причем
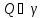 и секущая (3) переходит в касательную с
угловым коэффициентом
и секущая (3) переходит в касательную с
угловым коэффициентом
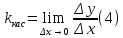
Пример.
Найдем касательную к кубической
параболе
 в точке
в точке
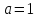 .
Имеем
.
Имеем

Отсюда
получаем ответ:
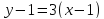 или
или
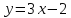 . Это и есть уравнение искомой касательной.
. Это и есть уравнение искомой касательной.
Определение. Предел
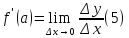
называется
производной функции
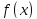 в точке
в точке
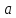 .
Функция
.
Функция
 называется дифференцируемой на интервале,
если она имеет производную в каждой
точке этого интервала.
называется дифференцируемой на интервале,
если она имеет производную в каждой
точке этого интервала.
Итак:
механический смысл производной --
мгновенная скорость. Геометрический
смысл производной -- тангенс угла наклона
касательной к графику функции в точке
в точке
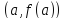 .
.
Уравнение касательной к графику
функции
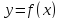 в
точке
в
точке
 имеет вид:
имеет вид:
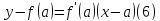
а уравнение нормали имеет вид:

в
предположении
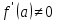 .
Если же
.
Если же ,
то касательная горизонтальна и задается
уравнением
,
то касательная горизонтальна и задается
уравнением
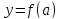 ,
а нормаль перпендикулярна оси Ох и
задается уравнением
,
а нормаль перпендикулярна оси Ох и
задается уравнением
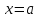 .
.
Примеры.
1.

2.
 .
Действительно,
.
Действительно,
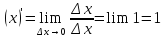
3.
 .
Действительно,
.
Действительно,
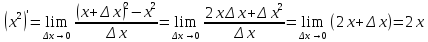
4.
Функция
 в нуле непрерывна, но не имеет производной.
Правая производная в нуле равна 1, а
левая равна
в нуле непрерывна, но не имеет производной.
Правая производная в нуле равна 1, а
левая равна
 .
.
Предложение. Дифференцируемая функция непрерывна.
Действительно,
из соотношения
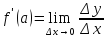 вытекает, что
вытекает, что
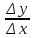 отличается от
отличается от
 на бесконечно малую величину
на бесконечно малую величину
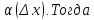
 и
и

Это
и означает непрерывность функции
 в точке
в точке
 .
□
.
□
Заметим,
что непрерывная функция не обязательно
будет дифференцируемой, см. выше пример
функции
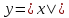 в точке
в точке
 .
.
-
Основные правила дифференцирования.
Д1. Производная константной функции равна нулю: (C)'=0.
Д2. Производная суммы равна сумме
производных:
 .
.
Д3. Постоянный множитель можно
выносить за знак производной:
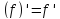 .
.
Д4. (правило Лейбница)
 .
.
Доказательство.

Здесь
мы применили правила предел суммы и
предел произведения, а также заменили
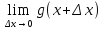 на
на
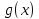 в виду непрерывности функции
в виду непрерывности функции
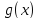 (см. предложение выше)
(см. предложение выше)
Д5.
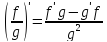 ;
в частности
;
в частности
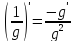 .
.
Д6.
(производная сложной функции})
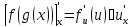
Обоснуем
эту формулу. Придадим приращение
 переменной
переменной
 .
Тогда
.
Тогда
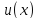 получит приращение
получит приращение
 Следовательно,
Следовательно,
 получит приращение
получит приращение
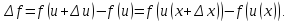 Далее:
Далее:

Замена
 на
на
 возможна в силу непрерывности
дифференцируемой функции
возможна в силу непрерывности
дифференцируемой функции
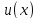 .
.
Д7. ( производная обратной функции})
Пусть
 -- две взаимно обратные функции. Тогда
-- две взаимно обратные функции. Тогда
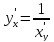 .
.
Действительно,
из
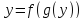 дифференцированием по
дифференцированием по следует соотношение
следует соотношение
 ,
откуда получаем результат.
,
откуда получаем результат.
Таблица производных
|
Функция |
|
|
|
|
|
|
|
|
|
|
Производная |
|
|
|
|
|
|
|
|
|
|
Функция |
|
|
|
|
|
|
|
|
|
Производная |
|
|
|
|
|
|
|
|
Здесь
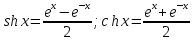 -- гиперболические синус и косинус
соответственно. Вычислим производную
синуса:
-- гиперболические синус и косинус
соответственно. Вычислим производную
синуса:

Здесь
мы воспользовались эквивалентностью
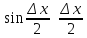 а также непрерывностью функции
а также непрерывностью функции
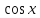 .
Вычислим производную косинуса:
.
Вычислим производную косинуса:

Здесь
мы воспользовались формулой производная
сложной функции, введя промежуточный
аргумент
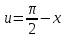 и учитывая
и учитывая
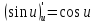 ,
а
,
а
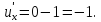 Производная тангенса:
Производная тангенса:
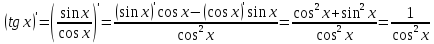
Производная экспоненты:
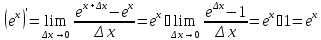
Производная
логарифма
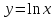 считается с применением правила
«производная обратной функции»
считается с применением правила
«производная обратной функции»
-
Другие приемы дифференцирования
-
Неявно заданные функции.
Пусть для уравнения

и
отрезков
 верно следующее: для любого
верно следующее: для любого
 найдется единственное значение
найдется единственное значение
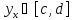 (зависящее от x) такое, что
(зависящее от x) такое, что
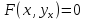 .
Тогда получаем закон
.
Тогда получаем закон
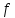 в силу которого любому
в силу которого любому
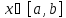 ставится в соответствие число
ставится в соответствие число
 такое, что
такое, что
 .
В этом случае
.
В этом случае
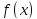 --
функция, заданная неявно уравнением
(1) в прямоугольнике
--
функция, заданная неявно уравнением
(1) в прямоугольнике
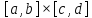 .
.
Пример. Соотнoшение
 в
области
в
области
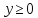 задает функцию
задает функцию
 ,
а в области
,
а в области
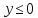 -- функцию
-- функцию
 .
.
Метод дифференцирования неявно заданных функций.
1.
Дифференцируем (1) по
 ,
считая
,
считая
 функцией аргумента x.
функцией аргумента x.
2.
Из полученного соотношения выражаем
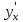 через y и x. Пусть результат будет
через y и x. Пусть результат будет
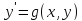
3.
Если даны координаты
 такие, что
такие, что
 ,
то
,
то
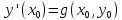 .
.
Пример.
Найдем производную функции, заданной
неявно соотношением
 в окрестности точки
в окрестности точки
 .
Дифференцируем данное отношение по
.
Дифференцируем данное отношение по
 ,
получим:
,
получим:
 .
Отсюда находим
.
Отсюда находим
 В точке
В точке
 эта производная равна
эта производная равна
 и уравнение касательной будет иметь
вид
и уравнение касательной будет иметь
вид
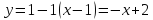
-
Параметрически заданные функции
Пусть

--
кривая на плоскости, заданная
параметрически. Предположим, что для
любого
 найдется единственное значение параметра
найдется единственное значение параметра
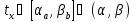 такое, что
такое, что
 .
Тогда
.
Тогда
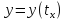 называется функцией, заданной
параметрически.
называется функцией, заданной
параметрически.
Пример. Соотношения
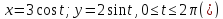
задают
эллипс с полуосями 3 и 2. Для любого x∈
[0,3] найдется единственное число
 ,
а именно
,
а именно
 такое,
что
такое,
что
 .
Тогда
.
Тогда
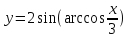 -- функция, заданная параметрически
соотношением (*), и которую в данном
случае мы записали как элементарную
функцию (другая запись той же функции
--
-- функция, заданная параметрически
соотношением (*), и которую в данном
случае мы записали как элементарную
функцию (другая запись той же функции
--
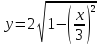 ).
).
Имеет место следующая формула, для производной функции, заданной параметрически:

Действительно,
дифференцируя
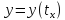 по
по
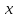 как сложную функцию с промежуточным
аргументом
как сложную функцию с промежуточным
аргументом
 ,
получаем
,
получаем
 Но
Но
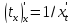 согласно правила дифференцирования
обратной функции. Подставляя, получим
согласно правила дифференцирования
обратной функции. Подставляя, получим
 ,
что и требовалось доказать.□
,
что и требовалось доказать.□
Пример.
Найдем касательную к эллипсу
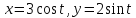 при
при
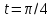 .
Значения функций
.
Значения функций
 ;
;


-
Логарифмическая производная
Пусть
задана дифференцируемая функция
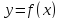 .
Тогда
.
Тогда
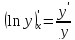 называют логарифмической производной
этой функции. Ясно, что
называют логарифмической производной
этой функции. Ясно, что
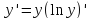 .
Иногда бывает проще сначала найти
логарифмическую производную.
.
Иногда бывает проще сначала найти
логарифмическую производную.
Пример.
Найдем производную функции
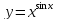 .
Сначала найдем логарифмическую
производную этой функции –
.
Сначала найдем логарифмическую
производную этой функции –
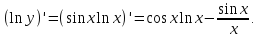
Отюда следует
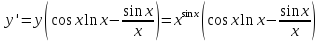
Теперь
найдем производную функции
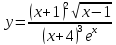 :
: