§ 4.4. Скалярный магнитный потенциал Скалярная краевая задача анализа магнитостатического поля

M_ф – фиктивная намагниченность среды;

–скалярный магнитный потенциал.

(1)

Уравнение (1) является уравнением магнитостатики относительно скалярного магнитного потенциала. Это уравнение может служить основой для постановки скалярной краевой задачи магнитостатики. Уравнение (1) дополняется следующими граничными условиями:

= поверхностное распределение – на части граничной поверхности Г₁;

B_n = поверхностное распределение – на части граничной поверхности Г₂;

Г = Г₁ + Г₂ – замкнутая граничная поверхность.

Уравнение (1) особенно удобно применять, когда источниками магнитного поля в расчетной области являются ненулевые граничные условия и остаточная магнитная индукция постоянных магнитов. В этом случае M_ф = 0. Если внутри расчетной области источники поля отсутствуют, то уравнение (1) приобретает вид

(2)

Если внутри расчетной области однородная по магнитным свойствам среда, то уравнение (2) сводится к уравнению Лапласа

Уравнение (2) можно применять для анализа магнитостатических полей, вызванных электрическими токами, в областях, где эти токи отсутствуют, поскольку там и . В этом случае при анализе может сказываться неоднозначность скалярного магнитного потенциала, связанная с ненулевым значением циркуляции вектора напряженности магнитного поля вдоль замкнутого контура, охватывающего электрический ток. Магнитное напряжение между двумя точками зависит от пути интегрирования напряженности магнитного поля

,

здесь n – целое любое число.

Фиктивная намагниченность среды в уравнении (1) вводится для преодоления проблемы неоднозначности скалярного магнитного потенциала. В частных случаях на каждый замкнутый контур, образуемый каждым током, натягивается тонкая непроницаемая перегородка, на которой поверхностно распределен магнитный диполь и на которой скалярный магнитный потенциал изменяется скачком. Если по контуру протекает ток I, то скачок потенциала на соответствующей перегородке равен

.

Моделирование магнитостатического поля цилиндрической катушки в pde Toolbox matlab

Схематичное изображение осевого сечения цилиндрической катушки без сердечника показано на рис. 6. Будем считать, что ток I течёт перпендикулярно плоскости сечения, и магнитный момент направлен вдоль оси x.

Рис. 6. Осевое сечение цилиндрической катушки

Общее уравнение магнитостатики относительно векторного магнитного потенциала имеет вид:

, (3)

где – относительная магнитная проницаемость вещества;A’– векторный магнитный потенциал, измеряемый в единицах тока; – векторное поле плотности тока; M_r – векторное поле остаточной намагниченности вещества. В рассматриваемом случае M_r=0, потому что в анализируемой системе нет постоянных магнитов.

Векторный потенциал и плотность тока можно выразить в цилиндрических координатах. Учитывая, что , (3) можно преобразовать в двумерную форму:

(4)

Поскольку магнитостатическое поле цилиндрической катушки симметричное, достаточно его рассчитывать только в первом квадранте системы координат (). Уравнение (4) можно решать непосредственно вPDETool относительно yA’. На рис. 7 показано распределение yA’ от катушки длиной l=32см, внутренним радиусом r_вн=3 см, наружным радиусом r_н=6 см, если ток I=2,5А, число витков w=3672. На рис. 8 показано распределение A’ от той же катушки.

Рис. 7. Распределение yA’

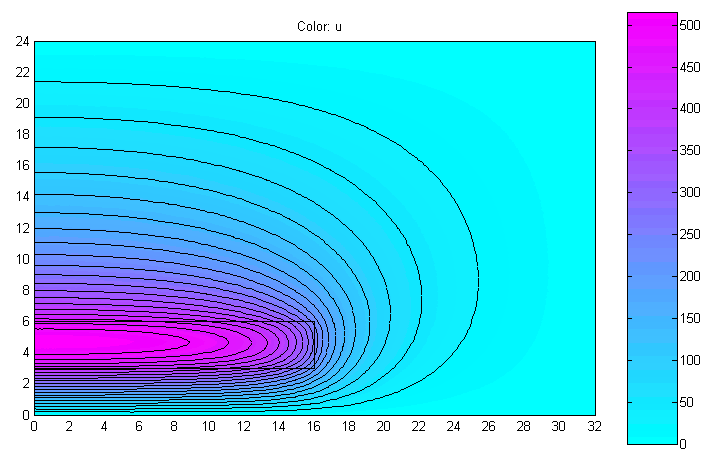
Рис. 8. Распределение A’

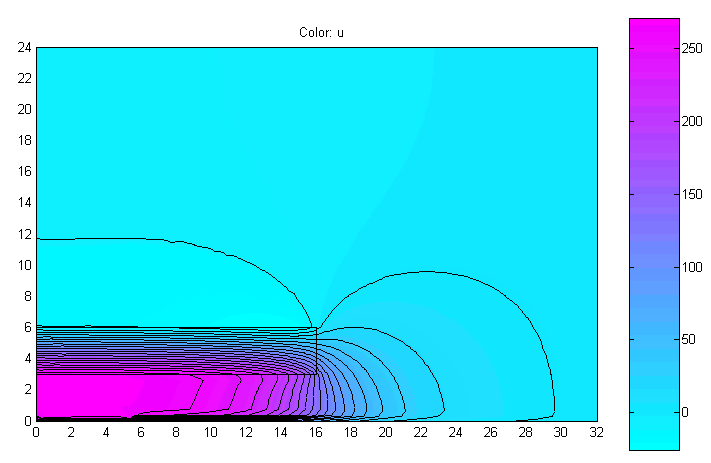
Рис. 9. Распределение x- составляющей напряжённости магнитного поля

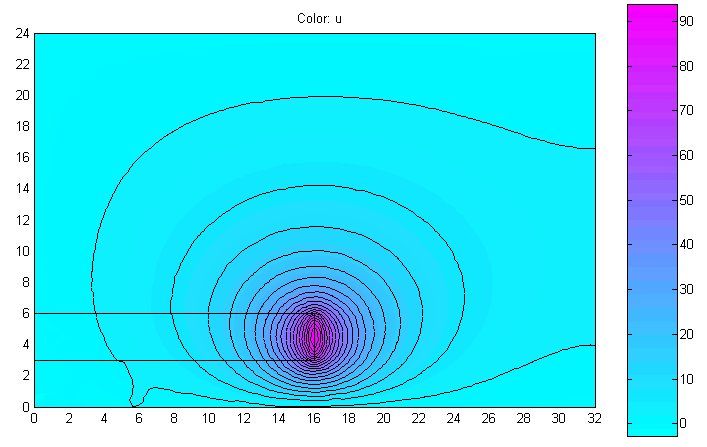
Рис. 10. Распределение y- составляющей напряжённости магнитного поля

На рис. 9, 10 показано распределение вектора напряжённости магнитного поля. Как видно, имеется некоторая численная неустойчивость при решении уравнения (4). Однако решение, данной краевой задачи удобно при вычислении потокосцеплений, а также собственных и взаимных индуктивностей. Например, магнитное потокосцепление в рассчитываемой катушке равно 0.58051Вб, а индуктивность L=0.58051/2.5=0.2322Гн.

Применительно к цилиндрической катушке большей численной устойчивостью обладает решение скалярной краевой задачи магнитостатики. Эта задача базируется на PDE относительно скалярного магнитного потенциала:

, (5)

где – скалярный потенциал напряжённости магнитного поля (скалярный магнитный потенциал);– абсолютная магнитная проницаемость вещества;M_ф – «фиктивная» намагниченность вещества, эквивалентирующая токи; B_r – вектор остаточной магнитной индукции постоянных магнитов; в случае с катушкой B_r=0.

Применительно к осесимметричному полю рассматриваемой катушки уравнение (5) в цилиндрических координатах имеет вид:

(6)

Уравнение (6) не может решаться в PDETool, поэтому для моделирования магнитного поля катушки написан специальный вычислительный сценарий. PDETool используется только для прорисовки геометрии и генерации конечноэлементной сетки.

Рис. 11. Распределение скалярного магнитного потенциала

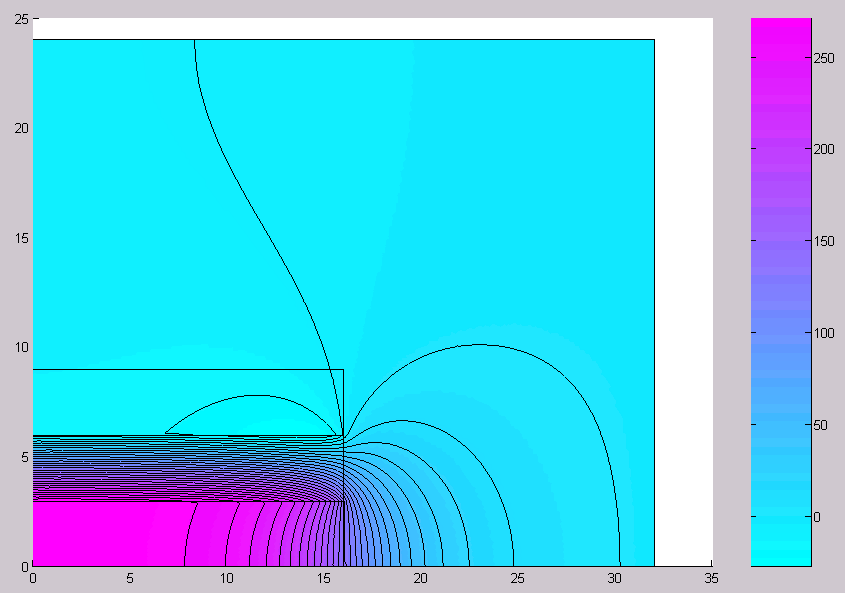
Рис. 12. Распределение x- составляющей напряжённости магнитного поля

Рис. 13. Распределение y- составляющей напряжённости магнитного поля

На рис. 11, 12, 13 показано распределение магнитостатического поля, рассчитанное путём решения уравнения (6). Эти рисунки показывают, что скалярная краевая задача магнитостатики в случае цилиндрической катушки обладает большей численной устойчивостью, чем векторная краевая задача. Потокосцепления и индуктивности удобнее выражать через векторный потенциал, а магнитные напряжения – через скалярный потенциал. Цилиндрическая катушка является наглядным примером зависимости магнитного напряжения между точками от пути, соединяющего эти точки. Магнитное напряжение между торцевыми точками катушки, лежащими на оси, равно 7824.9А, если путь лежит внутри канала, и 1355.1А, если путь лежит вне канала и вне области обмотки (эти числовые значения получены из анализа распределения скалярного потенциала).

Ниже приведён m-файл векторной магнитостатической модели цилиндрической катушки, предназначенный для загрузки в GUI-приложение PDETool.

function pdemodel

[pde_fig,ax]=pdeinit;

pdetool('appl_cb',1);

set(ax,'DataAspectRatio',[1 1.125 1]);

set(ax,'PlotBoxAspectRatio',[16 10.666666666666666 1]);

set(ax,'XLim',[0 32]);

set(ax,'YLim',[0 24]);

set(ax,'XTick',[ 0,...

2,...

4,...

6,...

8,...

10,...

12,...

14,...

16,...

18,...

20,...

22,...

24,...

26,...

28,...

30,...

32,...

]);

set(ax,'YTick',[ 0,...

2,...

4,...

6,...

8,...

10,...

12,...

14,...

16,...

18,...

20,...

22,...

24,...

]);

pdetool('gridon','on');

% Geometry description:

pderect([0 16 3 6],'R1');

pderect([0 32 24 0],'R2');

set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','R1+R2')

% Boundary conditions:

pdetool('changemode',0)

pdesetbd(9,...

'neu',...

1,...

'0',...

'0')

pdesetbd(8,...

'neu',...

1,...

'0',...

'0')

pdesetbd(7,...

'neu',...

1,...

'0',...

'0')

pdesetbd(6,...

'dir',...

1,...

'1',...

'0')

pdesetbd(5,...

'dir',...

1,...

'1',...

'0')

pdesetbd(4,...

'dir',...

1,...

'1',...

'0')

% Mesh generation:

setuprop(pde_fig,'Hgrad',1.3);

setuprop(pde_fig,'refinemethod','regular');

pdetool('initmesh')

pdetool('refine')

pdetool('refine')

pdetool('refine')

% PDE coefficients:

pdeseteq(1,...

'y.^-1!y.^-1',...

'0.0!0.0',...

'0.0!2.5*3672/3/32',...

'1.0!1.0',...

'0:10',...

'0.0',...

'0.0',...

'[0 100]')

setuprop(pde_fig,'currparam',...

['y.^-1!y.^-1 ';...

'0.0!0.0 ';...

'0.0!2.5*3672/3/32';...

'1.0!1.0 '])

% Solve parameters:

setuprop(pde_fig,'solveparam',...

str2mat('0','23904','10','pdeadworst',...

'0.5','longest','0','1E-4','','fixed','Inf'))

% Plotflags and user data strings:

setuprop(pde_fig,'plotflags',[4 1 1 1 1 1 1 0 0 0 0 1 1 1 0 0 0 1]);

setuprop(pde_fig,'colstring','u./y');

setuprop(pde_fig,'arrowstring','');

setuprop(pde_fig,'deformstring','');

setuprop(pde_fig,'heightstring','');

% Solve PDE:

pdetool('solve')

% figure(2)

% uu=u; uu(find(p(2,:)))=u(find(p(2,:).'))./p(2,find(p(2,:).')).';

% pdeplot(p,e,t,'xydata',uu,'contour','on','levels',30,'colormap','hsv')

% [uux,uuy]=pdegrad(p,t,uu);

% hx=uu; hx(find(p(2,:)))=uu(find(p(2,:).'))./p(2,find(p(2,:).')).'; hx=hx+pdeprtni(p,t,uuy);

% hy=-pdeprtni(p,t,uux);

% pdeplot(p,e,t,'xydata',hx,'contour','on','levels',30,'colormap','hsv')

% pdeplot(p,e,t,'xydata',hy,'contour','on','levels',30,'colormap','hsv')

Здесь последние операторы, переведённые в комментарии, предназначены для визуализации векторного потенциала и компонентов напряжённости магнитного поля (рис. 8, 9, 10). Их нужно выполнять после экспорта из PDETool в рабочую область MATLAB конечноэлементной сетки и решения краевой задачи.

Ниже приведён текст m-файла геометрической модели цилиндрической катушки, предназначенной для решения скалярной краевой задачи магнитостатики.

function pdemodel

[pde_fig,ax]=pdeinit;

pdetool('appl_cb',1);

set(ax,'DataAspectRatio',[1 1.125 1]);

set(ax,'PlotBoxAspectRatio',[16 10.666666666666666 1]);

set(ax,'XLim',[0 32]);

set(ax,'YLim',[0 24]);

set(ax,'XTick',[ 0,...

2,...

4,...

6,...

8,...

10,...

12,...

14,...

16,...

18,...

20,...

22,...

24,...

26,...

28,...

30,...

32,...

]);

set(ax,'YTick',[ 0,...

2,...

4,...

6,...

8,...

10,...

12,...

14,...

16,...

18,...

20,...

22,...

24,...

]);

pdetool('gridon','on');

% Geometry description:

pderect([0 16 3 6],'R1');

pderect([0 16 0 3],'R2');

pderect([0 16 6 9],'R3');

pderect([0 32 24 0],'R4');

set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','R1+R2+R3+R4')

После загрузки этого m-файла в PDETool нужно сгенерировать конечноэлементную сетку и экспортировать её в рабочую область MATLAB. Затем можно запускать следующий вычислительный сценарий.

% Kats - скалqрный магнитный потенциал вокруг цилиндрической катушки

% Геометриq описана в katushkas.m

% Запускать только после экспорта в рабочую область

ye=pdeintrp(p,t,p(2,:).');

c=ye;

a=zeros(1,size(t,2));

f=a;

[k,f1]=assempde('bKats',p,e,t,c,a,f);

iee=find((e(6,:)==2&e(7,:)==1)|(e(7,:)==2&e(6,:)==1));

f1(e(1,iee))=f1(e(1,iee))+2.5*3672/32*0.5*abs(p(2,e(1,iee))-p(2,e(2,iee))).'.*mean([p(2,e(1,iee));p(2,e(2,iee))]).';

f1(e(2,iee))=f1(e(2,iee))+2.5*3672/32*0.5*abs(p(2,e(1,iee))-p(2,e(2,iee))).'.*mean([p(2,e(1,iee));p(2,e(2,iee))]).';

iee=find(e(5,:)==7);

f1(e(1,iee))=f1(e(1,iee))+(2.5*3672/32*((6-p(2,e(1,iee)))/3*2+(6-p(2,e(2,iee)))/3)/6 ...

.*abs(p(2,e(1,iee))-p(2,e(2,iee)))).'.*mean([p(2,e(1,iee));p(2,e(2,iee))]).';

f1(e(2,iee))=f1(e(2,iee))+(2.5*3672/32*((6-p(2,e(2,iee)))/3*2+(6-p(2,e(1,iee)))/3)/6 ...

.*abs(p(2,e(1,iee))-p(2,e(2,iee)))).'.*mean([p(2,e(1,iee));p(2,e(2,iee))]).';

u=k\f1;

figure(1);

pdeplot(p,e,t,'xydata',u,'contour','on','levels',30,'colormap','cool')%'hsv')

[ux,uy]=pdegrad(p,t,u);

hxe=-ux;

hxe(t(4,:)==2)=hxe(t(4,:)==2)+2.5*3672/32;

hxe(t(4,:)==3)=hxe(t(4,:)==3)+2.5*3672/32*(6-ye(t(4,:)==3))/3;

hx=pdeprtni(p,t,hxe);

hy=pdeprtni(p,t,-uy);

figure(2);

pdeplot(p,e,t,'xydata',hx,'contour','on','levels',30,'colormap','cool')%'hsv')

figure(3);

pdeplot(p,e,t,'xydata',hy,'contour','on','levels',30,'colormap','cool')%'hsv')

function [q,g,h,r]=bKats(p,e,u,time)

q=zeros(1,size(e,2));

g=q;

h=[q q];

r=h;

ih=find(p(1,e(1,:))==0&p(1,e(2,:))==0);

h(ih)=ones(1,length(ih));

h((size(e,2)+1):end)=h(1:size(e,2));

В результате выполнения этого сценария в фигурах MATLAB будут получены картины поля, изображённые на рис. 11, 12, 13.