Потокосцепление. Собственная и взаимная индуктивности

Согласно закону электромагнитной индукции в контуре, охватывающем переменный магнитный поток, индуцируется ЭДС

Если контур состоит из w витков одного направления намотки, и все они сцеплены с одним и тем же потоком, то ЭДС отдельных витков суммируются арифметически и результирующая ЭДС равна

Произведение называют магнитным потокосцеплением.

Пусть контур выполнен из тонкого провода, а магнитное поле возбуждено собственным током I этого контура. Тогда потокосцепление в этом контуре пропорционально току, если окружающая среда обладает линейными магнитными свойствами . Коэффициент пропорциональностиL называют собственной индуктивностью контура или цепи.

Можно доказать, что энергия магнитного поля этого контура равна

.

В случае двух индуктивно связанных контуров с токами I₁ и I₂ можно получить выражение для энергии магнитного поля в виде:

, (3)

где и– потокосцепления контуров, вызванные собственными токамиI₁ и I₂,

и – потокосцепления взаимной индукции, обусловленные токамиI₁ и I₂ соответственно, и пропорциональные им в случае линейных магнитных свойств среды:

;

;

M₁₂ = M₂₁ = M,

M – взаимная индуктивность контуров или цепей. Знаки «+» или «–» в выражении (3) зависят от способа включения контуров – согласного или встречного.

Если контуры окружает однородная среда, то

Вычисление взаимной индуктивности круглых и прямоугольных контуров в системе matlab

Ниже приведены тексты вычислительных сценариев расчёта взаимной индуктивности пар круглых и прямоугольных соосно расположенных в пространстве контуров.

% vzindkr - расчёт взаимной индуктивности круглых катушек

%

% Входные данные;

% R1 - радиус первой катушки

% R2 - радиус второй катушки

% w1 - число витков первой катушки

% w2 - число витков второй катушки

% x - массив расстояний между центрами катушек

% Выходные данные;

% M - массив взаимных индуктивностей катушек

m0=4E-7*pi;

k=2*sqrt(R1*R2./((R1+R2)^2+x.^2));

[K,E]=ellipke(k.^2);

M=m0*w1*w2*sqrt(R1*R2)*((2./k-k).*K-(2./k).*E);

% vzindpr - расчёт взаимной индуктивности прямоугольных катушек

%

% Входные данные;

% a - длина прямоугольного контура катушки

% b - ширина прямоугольного контура катушки

% w1 - число витков первой катушки

% w2 - число витков второй катушки

% x - массив расстояний между центрами катушек

% Выходные данные;

% M - массив взаимных индуктивностей катушек

m0=4E-7*pi;

M11=m0*a/pi/2*(log((a+sqrt(a^2+x.^2))./x)-(sqrt(a^2+x.^2)-x)/a);

M22=m0*b/pi/2*(log((b+sqrt(b^2+x.^2))./x)-(sqrt(b^2+x.^2)-x)/b);

M13=m0*a/pi/2*(log((a+sqrt(a^2+b^2+x.^2))./sqrt(b^2+x.^2))-(sqrt(a^2+b^2+x.^2)-...

sqrt(b^2+x.^2))/a);

M24=m0*b/pi/2*(log((b+sqrt(a^2+b^2+x.^2))./sqrt(a^2+x.^2))-(sqrt(a^2+b^2+x.^2)-...

sqrt(a^2+x.^2))/b);

M=2*w1*w2*(M11+M22-M13-M24);

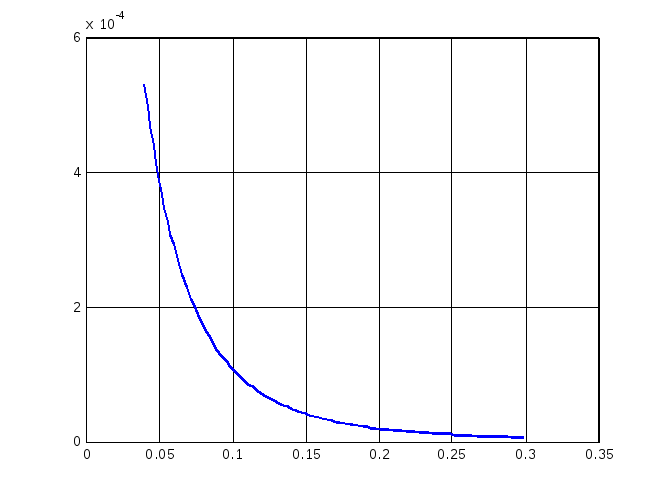
Для примера запустим один из этих сценариев.

>> R1=0.048; R2=0.048;

>> w1=132; w2=132;

>> x=[0.04:0.002:0.06, 0.06:0.003:0.3]; % расстояния в метрах

>> vzindkr % Взаимные индуктивности, Гн

>> plot(x,M)

>> grid on

Контрольные вопросы

1. Как выражается магнитный поток через векторный потенциал?

2. Как выражается энергия магнитостатического поля через векторный потенциал?

3. Что такое магнитное потокосцепление и как с ним связана ЭДС электромагнитной индукции?

4. Что такое индуктивность контура и как она связана с энергией магнитного поля?

5. Что такое взаимная индуктивность двух контуров?

6. По какой формуле вычисляется взаимная индуктивность двух контуров, находящихся в бесконечной однородной среде?