4. Рекурсия

Последовательность объектов, взятых из множестваесть не что иное как отображениесопоставляющее каждому натуральному числуобъект.

Пусть нам дано отображение и первый член последовательности. Определим последовательностьтак, что

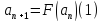
Это фактически есть определение по индукции, где база индукции есть явное задание первого члена последовательности, а индукционный переход есть соотношение (1).

Примеры. Один из способов определения натуральных чисел таков:

Тот факт, что все эти объекты можно объединить в одно бесконечное множество есть одна из аксиом теории множеств. В этом множестве имеется операция прибавления единицы. Арифметические операции сложения, умножения, возведения в степенб, факториала определяются рекурсивно (или, по-другому, индуктивно):

• Определение сложения: и

• Определение умножения: и

• Определение степени: и

• Определение факториала: и

Доказательства стандартных свойств этих операций – многократное применение ПМИ.

Бывает и более сложная рекурсия, когда задаются явно первые два члена последовательности – , а каждый следующий вычисляется по предыдущим двум по фиксироыванной схеме:

Здесь -- заданное отображение.

Пример – числа Фибоначчи

Несколько первых чисел Фибоначчи таковы

Явная формула для чисел Фибоначчи существует и имеет вид

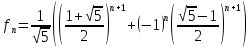
Докажем это. Будем искать числа 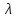такие, чтодля всех натуральных. Сокращяя наполучаем квадратное уравнение(называемое характеристическим), корни которого суть. Любая линейная комбинация степеней, т.е. последовательность видатакже будет удовлетворять рекурентному соотношению. Остается выбратьитак, чтобы удовлетворить начальным условиям:

Отсюда и,.

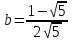5. Суммы, произведения и бином Ньютона

Этот вспомогательный параграф содержит чрезвычайно часто употребляемые в математике операторы суммирования и произведения, а также формулу бинома Ньютона, обобщающую известные формулы квадрат суммы и куб суммы двух чисел.

Пусть задано конечное семейство чисел . Тогда выражениеобозначает их сумму, а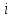называется индексом суммирования, который пробегает от 1 до n. Аналогично,обозначает произведениесемейства чисел. Если мы заменим индекс суммирования на любую другую букву, то результат применения операторов суммирования и произведения не изменится. Строго, суммаопределяется рекурсивно по последовательностикак

Аналогично

Если все числа из семейства равны одному и тому же числу d, тои. Отметим свойство линейности суммы:

В этом смысле оператор суммирования проще (и чаще употребительней) оператора произведения, свойство линейности для последнего не выполняется.

Факториал натурального числаn есть произведение всех натуральных чисел от 1 до n включительно. Обозначается факториал как n!. Полагаем также по определению 0!=1. Получаем

Подсчет 1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720, 7!=5040, 8!=40320, … убеждает нас, что факториал -- очень быстро растущая функция.

Решим теперь такую комбинаторную задачу: сколькими способами можно выбрать k предметов из n предметов. Обозначим это число (читается: "це из эн по ка"). В некоторых частных случаях ответ прост:,,. Формулаполучается после некоторого размышления -- выбор n-1 предмета из n предметов равносилен "невыбору" одного предмета из тех же n предметов. Иными словами. Обобщая это правило на случай k предметов, получим:

Фиксируем один предмет среди данных n предметов A. Тогда все выборы k предметов из A, т.е. все подмножества B⊆A содержащие k предметов разбиваются на два класса -- те, что содержати те, что не содержат. В первом классеподмножеств (остается выбрать k-1 предмет из), а во втором классеподмножеств (все k предметов выбираем из множества). Получаем:

Этой формулой можно пользоваться для всех 1≤ k≤ (n-1) и n≥ 1. Вместе с "граничными условиями" это дает способ вычисления всех чисел. Соотношения (3) также представляют собой рекуррентные формулы.

Получаем так называемый треугольник Паскаля

1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 ..... .. .. .. .. .. .. .. .. .. .. .. .....

В этом треугольнике n-ая строка сверху содержит числаприk=0,1,2,… ,n. Любое число, кроме самых крайних слева и справа равно сумме чисел стоящих над ним (4=1+3, 6=3+3, и.т.д.) Имеется и прямая, не рекуррентная формула для чисел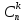

Предложение.Для всех n≥ 1 и всех 0≤ k≤ n имеет место равенство

Доказательство. Обозначим пока . Имеем:

Иными словами, краевые условия совпадают. Докажем, что числа удовлетворяют рекуррентному соотношению (3).

Теперь очень легко индукцией по n доказать, что имеет место равенство для всех допустимых k. Действительно, база индукции, n=1 проверяется прямым подсчетом. Предполагая далее верным равенствопри всехдокажем равенстводля всех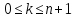. Во-первых, это так дляи для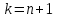в силу совпадения граничных условий. Для остальных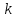воспользуемся рекуррентным соотношением и предположением индукции:

Бином Ньютона. Для любого натурального n имеет место равенство

Доказательство. Раскрывая скобки в произведении

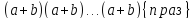
мы видим, что количество слагаемых, у которых степень по равна, а степень поравнасовпадает с числом выборовпредметов из n предметов, т.е. с.

Возможен и другой способ доказательства бинома Ньютона -- индукцией по степени n. Тогда следует применить рекуррентные формулы (3). В связи формулой бинома Ньютона числа называютбиномиальными коэффициентами.

Пример

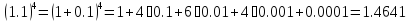
Крупное достижение Ньютона состоит в том, что формулой (5) можно пользоваться и в случае нецелого . Правда в этом случае справа получается бесконечная сумма:

Точное значение 1,0488088481701515469914535136799…

23