
Мощность множества
Множества
 и
и равномощны(или, упрощенно, имеют
одно и то же количество элементов), если
найдется биекция одного из этих множеств
на другое. Равномощность есть отношение
эквивалентности на классе всех множеств.
равномощны(или, упрощенно, имеют
одно и то же количество элементов), если
найдется биекция одного из этих множеств
на другое. Равномощность есть отношение
эквивалентности на классе всех множеств.
Множество
 равномощное своей собственной части
(например, подмножеству
равномощное своей собственной части
(например, подмножеству ,
где
,
где
 какой-либо элемент из
какой-либо элемент из )
называется бесконечным. В противном
случае, если не существует биекции между
)
называется бесконечным. В противном
случае, если не существует биекции между и
и
 ,
множество
,
множество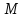 называется конечным. Пример конечных
множеств – натуральные числа, которые
определяются индуктивно
называется конечным. Пример конечных
множеств – натуральные числа, которые
определяются индуктивно
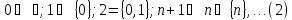
Тот
факт, что этот индуктивный процесс можно
считать завершенным и образовать тем
самым множество
 натуральных чисел с нулем вытекает изаксиомы бесконечности:существует
бесконечное множество.
натуральных чисел с нулем вытекает изаксиомы бесконечности:существует
бесконечное множество.
Множество
 ,
равномощное совокупности натуральных
чисел, называется счетным, ибо его
элементы без пропусков и повторений
можно выписать как последовательность
,
равномощное совокупности натуральных
чисел, называется счетным, ибо его
элементы без пропусков и повторений
можно выписать как последовательность
Докажем,
что множество действительных чисел на
отрезке
 не счетно и тем самым имеет большую
мощность чем
не счетно и тем самым имеет большую
мощность чем .
Предположим противное:
все действительные числа из отрезка
.
Предположим противное:
все действительные числа из отрезка можно занумеровать:
можно занумеровать:

(здесь
все
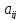 -- цифры). Построим число
-- цифры). Построим число так, что
так, что и
и для каждого разряда
для каждого разряда .
Но тогда
.
Но тогда ,
число из отрезка
,
число из отрезка ,
не содержится в списке (3). Это противоречие
с допущением показывает, что действительные
числа из отрезка
,
не содержится в списке (3). Это противоречие
с допущением показывает, что действительные
числа из отрезка нельзя перенумеровать, их больше чем
натуральным чисел.
нельзя перенумеровать, их больше чем
натуральным чисел.
С
другой стороны, декартов квадрат
 -- счетное множество, ибо элементы таблицы
чисел
-- счетное множество, ибо элементы таблицы
чисел

можно
перенумеровать «змейкой» как показано
выше. Из этого факта довольно просто
следует, что множество всех дробей
 ,
т.е. множество рациональных чисел также
счетно.
,
т.е. множество рациональных чисел также
счетно.
Индукция
Метод математической индукции иначе еще называют принципом домино. Представим себе ряд костей домино. Если толкнуть первую кость, то она вызовет падение второй кости, а та в свою очередь третьей и т.д. пока все кости не упадут. Разрушение всей системы основано на двух фактах:
1) первую кость мы толкаем сами, 2) если кость с номером n падает, то она вызывает падение и кости с номером n+1.
Принцип математической индукции гласит, что даже если в ряду костей домино бесконечное число, то все кости упадут. Трудность состоит в том, чтобы мыслить этот процесс завершенным до конца. Ясно, что никакой реальный эксперимент не может подтвердить такой принцип в точности, но частичное подтверждение этого принципа есть -- результат падения всех костей, даже если их несколько тысяч.
Приведу пример доказательства "по индукции" из теории чисел. Докажем, что для любого натурального n выполняется равенство

Нам надо обосновать целую серию числовых равенств
(Р1)
 (Р2)
(Р2)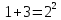 (Р3)
(Р3) ......................
(Рn)
......................
(Рn)
(Р(n+1)) .....................
.....................
Что касается первых несколько, то они очевидны и в справедливости их можно убедиться непосредственным вычислением. Но ведь нам надо доказать соотношение (1) сразу для всех n. Поступим так: примем на веру, что утверждение Рn справедливо. Тогда преобразования

убеждают нас, что и следующее утверждение Р(n+1) также верно. Мы попадем в ситуацию, как и с костями домино: первое утверждение проверили, из него вытекает второе, а из него вытекает третье и т.д. до конца. Вот в этом слове "до конца" вся трудность -- конца-то у последовательности натуральных чисел нет. Здесь мы должны прочувствовать и поверить, что если в серии доказываемых равенств первое равенство верно, а из справедливости равенства с номером n вытекает справедливость n+1-го равенства, то все равенства верны. Иными словами мы считаем процесс выведения следующего равенства из предыдущего завершенным.
Наряду с формулой (1) будем далее пользоваться формулами:
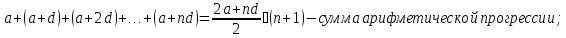
В частности
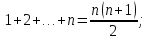

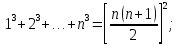
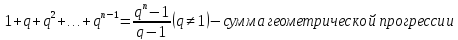
Все эти формулы можно доказать «по индукции».
Отчетливо и строго принцип математической индукции сформулирован в параграфе «Методы доказательств»
Иногда
ПМИ применяется в другой форме: если
для ряда утверждений
 , проверена база индукции, а также
установлено, что из того, что все
утверждения
, проверена база индукции, а также
установлено, что из того, что все
утверждения справедливы для всех k<n вытекает
справедливость n-го утверждения
справедливы для всех k<n вытекает
справедливость n-го утверждения ,
то как и ранее заключаем, что утверждения
,
то как и ранее заключаем, что утверждения верны для всех n.
верны для всех n.
Приведем пример утверждения из теории делимости натуральных чисел, где при доказательстве используется ПМИ во второй редакции. А именно, докажем основную теорему арифметики: любое натуральное число n>1 разложимо в произведение простых чисел и такое разложение единственно с точностью до перестановки множителей.
База индукции -- случай n=2. Это наименьшее простое число. Для него теорема верна. Предположим, что мы проверили разложимость в произведение простых всех чисел k меньший n. Если n ни на что не делится, кроме самого себя и единицы, то n -- простое число и n является искомым разложением самого себя. В противном случае, n=k⋅m для натуральных чисел 1<k, m<n. По предположению индукции числа k и m разложимы в произведение простых. Следовательно, и их произведение n также разложимо в произведение простых.
Единственность
разложения доказываем методом от
противного. Пусть
 -- простое число, входящее в разложение
числа
-- простое число, входящее в разложение
числа и в то же время
и в то же время ,
где все
,
где все -ые
простые числа не равные
-ые
простые числа не равные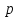 .
Считаем
.
Считаем наименьшим возможным с таким свойством.
Поделим каждый
наименьшим возможным с таким свойством.
Поделим каждый на
на с остатком
с остатком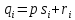 .
Здесь
.
Здесь в силу
в силу .
Тогда раскрывая скобки в произведении
.
Тогда раскрывая скобки в произведении и перенося все слагаемые с множителем
и перенося все слагаемые с множителем в левую часть равенства
в левую часть равенства получим равенство
получим равенство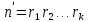 где левая часть имеет в разложении на
простые множители число
где левая часть имеет в разложении на
простые множители число ,
а правая в разложении на простые множители
имеет простые сомножители меньшие
,
а правая в разложении на простые множители
имеет простые сомножители меньшие ,
ибо сами
,
ибо сами -ые
меньше
-ые
меньше .
Следовательно, приходим к противоречию
с минимальностью
.
Следовательно, приходим к противоречию
с минимальностью (Случай, когда все
(Случай, когда все быть не может, так как
быть не может, так как делится на
делится на ).
Противоречие показывает, что если в
одном из разложений натурального числа
).
Противоречие показывает, что если в
одном из разложений натурального числа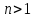 встречается простое число
встречается простое число ,
то в любом другом разложении оно также
встречается. Сокращая на
,
то в любом другом разложении оно также
встречается. Сокращая на ,
приходим к разложениям с меньшим числом
простых сомножителей. Индукция по числу
простых сомножителей завершает
доказательство.
,
приходим к разложениям с меньшим числом
простых сомножителей. Индукция по числу
простых сомножителей завершает
доказательство.
