3. Отображения

Отношением между множествамииназывается подмножество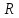декартова произведения. При этом отношение задается либо словесно, либо формулой но формальносовпадает с тройкой. Говорим, что элементнаходится в отношенииcэлементоми пишем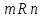, если. Определим важнейшие типы отношений.

Отношение β вида , гденазываютотношением на множестве. При этом

• βназываетсярефлексивным, еслидля любого;

• βназываетсятранзитивным, если изивытекает, что;

• βназываетсяантисимметричным, если изивытекает равенство;

• βназываетсяотношением частичного порядка, или простопорядком, если оно рефлексивно, транзитивно и антисимметрично;

• βназываетсяотношением эквивалентности, если оно рефлексивно, симметрично и транзитивно

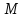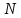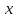Отношение такое, что для любогонайдется единственная парас некоторымназываетсяотображением из в. При этомназываетсяграфикомэтого отображения. Неформально, отображениеммножествав множество(обозначается) называется правило, в силу которого каждому элементуставится в соответствие единственный элемент. При этом множествоназываетсяобластью определения (ОДЗ),--областью прибытия,--аргументом, а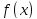--значением отображения на элементе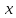илиобразом элемента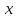при отображении.Графиком отображенияназывается совокупность всех пар, когда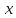пробегает ОДЗ. Формально:

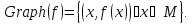
Говорят, что отображение взаимно однозначно,если разным значениям аргумента соответствуют разные значения отображения. Это эквивалентно следующему условию:

Множество

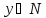называется областью значенийотображения. Очевидно, чтоесть подмножество множества N. Если, т.е. если для всякогонайдется хотя бы один аргумент(прообраз) такой, что, тоназовем отображением множестваMна множество N.

Можно задавать отображение таблицей из двух строк, где в первой строке перечислены все возможные аргументы, а во второй – соответствующие им значения. Если и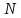числовые множеств, то отображениеназывают более точно --функцией. В этом случае чаще прибегают к аналитическому способу задания функции. Функция задается аналитическим выражением, в которое входят переменная, константы и известные и точно определенные операции (арифметические, корни, логарифмы, показательные функции, тригонометрические и т.п.)Естественной ОДЗ аналитическоговыражения называется совокупность всех чисел, при которых все операции, входящие в аналитическое выражение определены, и получается итоговый результат --

Мы рассмотрели два способа задания отображений – табличный и аналитический. Вообще говоря, правило задающие отображение может быть весьма причудливым -- например, отображение Pi из множества ℕнатуральных чисел в множество цифр {0,1,… ,9} такое, что Pi(n) есть цифра, стоящая на n-ом месте в десятичной записи числа π (Pi(1)=1, Pi(2)=4 и т.д.). С другой стороны, правило сопоставляющее натуральному числу n его делитель, не является функцией, ибо отсутствует однозначность образа -- у числа может быть несколько делителей.

Композицией отображенийиназывается отображениетакое, чтодля всех. В этом случае функциюназывают также подстановкой функциив функцию. Например, функцияполучается подстановкой в функциюфункции. Заметим, что композиция подчиняетсязакону ассоциативности: если кромеиимеется еще отображение, то

Действительно, применяя левую и правую часть этого соотношения к элементу , получаем в обоих случаях.

Отображение , сопоставляющее элементусам этот элементназываетсятождественным. Обозначим его. Оно играет роль единичного элемента для отображений. А именно дляимеют место равенства

Взаимно однозначное отображение и одновременно отображение "на" называется биективным, илибиекцией.Например, тождественное отображение будет биекцией.

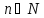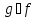Отображение является биекцией в том и только том случае, когда существует отображение, называемоеобратным, такое, чтои-- тождественные отображения. Обоснуем это. Пусть-- биекция. Определимтак, что, если элементпроизволен, то-- тот единственный элемент, для которого. Легко проверить, чтои-- тождественные отображения. Наоборот, пустьи-- тождественные отображения для некоторого. Если, тои взаимная однозначность следует. Далее, если-- произвольный элемент, тотот элемент из, для которого. Это доказывает, чтоесть отображение "на".