
Множества. Логика.
1Логика 1
1.1Полные и противоречивые теории 3
1.2Методы доказательств. 4
2Множества 6
3Отображения 9
1.3Мощность множества 12
4Индукция 14
1.4Рекурсия 17
5Суммы, произведения и бином Ньютона 19
Логика
Математика имеет дело с математическими объектами такими, как, например, числа, вектора, матрицы, функции, прямые, плоскости, геометрические фигуры и т.п. и т.д. Эти объекты связаны между собой огромным количеством отношений и свойств: равно, больше, меньше, делится (для чисел), возрастает, убывает, выпукла, вогнута (для функций); параллельны, перпендикулярны (для прямых) и т.д. Математический текст состоит из утверждений. Математическим утверждением называется повествовательное предложение, что-либо «утверждающее» относительно математических объектах и о котором хотя бы в принципе можно сказать верно оно или не верно. Например,
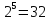 ;
;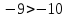 ;
;любые две прямые на плоскости пересекаются;
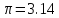
суть
утверждения первые два из которых верны,
а последние два не верны. В то же время,
словосочетание « »
не является утверждением, это есть
объект – число 4. Словосочетание «
»
не является утверждением, это есть
объект – число 4. Словосочетание «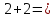 »
синтаксически не корректно и поэтому
не является ни утверждением, ни объектом.
»
синтаксически не корректно и поэтому
не является ни утверждением, ни объектом.
Пусть
 -- какие-либо утверждения. Из них можно
построить новые утверждения, пользуясь
логическими операциями «и», «или», «не»,
«следует», «эквивалентно». Утверждение
-- какие-либо утверждения. Из них можно
построить новые утверждения, пользуясь
логическими операциями «и», «или», «не»,
«следует», «эквивалентно». Утверждение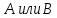 истинно в том и только том случае, если
истинно одно из утверждений
истинно в том и только том случае, если
истинно одно из утверждений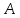 или
или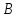 (или оба вместе). Например, утверждение
(или оба вместе). Например, утверждение ,
эквивалентное “
,
эквивалентное “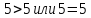 ”
истинно, так как вторая компонента
связки «или» выполнена. Утверждение
”
истинно, так как вторая компонента
связки «или» выполнена. Утверждение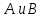 истинно в том и только том случае, если
истинно как утверждение
истинно в том и только том случае, если
истинно как утверждение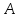 так и
так и .
Отрицание утверждения
.
Отрицание утверждения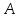 обозначаем как
обозначаем как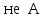 ,
оно истинно, если и только если
,
оно истинно, если и только если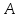 ложно.
ложно.
Импликация
 значит,
что из утверждения
значит,
что из утверждения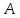 следует (вытекает) утверждение
следует (вытекает) утверждение .
Импликация ложна только в одном случае,
когда посылка
.
Импликация ложна только в одном случае,
когда посылка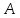 истинная, а заключение
истинная, а заключение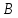 ложно. В частности, импликация
ложно. В частности, импликация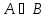 эквивалентна утверждению «
эквивалентна утверждению «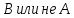 ».
С импликацией связано единственное
правило вывода (modusponens):
если утверждение
».
С импликацией связано единственное
правило вывода (modusponens):
если утверждение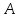 верно, а также истинна импликация
верно, а также истинна импликация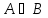 ,
то и утверждение
,
то и утверждение также верно. Выводятся (доказываются)
утверждения исходя из аксиом. Аксиома
также является математическим
утверждением, справедливость которого
принимается на веру.
также верно. Выводятся (доказываются)
утверждения исходя из аксиом. Аксиома
также является математическим
утверждением, справедливость которого
принимается на веру.
Запись
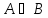 значит, что эти утверждения эквивалентны,
т.е. справедливость одного влечет
справедливость другого.
значит, что эти утверждения эквивалентны,
т.е. справедливость одного влечет
справедливость другого.
Тавтологией
называется утверждение верное при любой
интерпретации входящих в него логических
переменных. Простейшая из них
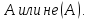 Приведем примеры других тавтологий.
Пусть
Приведем примеры других тавтологий.
Пусть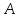 и
и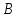 -- два утверждения. Тогда
-- два утверждения. Тогда
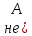 и
и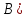 ⇔не(
⇔не(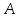 )
или не (
)
или не (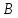 );
);
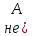 или
или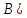 ⇔не(
⇔не(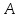 )
и не (
)
и не (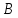 );
);
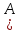
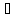
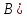 ⇔ ( не (
⇔ ( не ( )
) не(
не(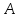 ));
(1)
));
(1)
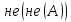 ⇔
⇔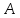 -- «отрицание отрицания»
-- «отрицание отрицания»
Пример. Утверждение «не верно, что кот Васька плут и мошенник» эквивалентно следующему: «или Васька не плут или Васька не мошенник». Утверждение «не верно, что Фигаро здесь или Фигаро там» эквивалентно следующему: «Фигаро и не здесь и не там».
Следует
привыкнуть и к так называемым кванторам
существования и всеобщности. Запись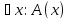 значит, что существует элемент
значит, что существует элемент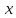 (он может быть не единственен), что
выполняется условие
(он может быть не единственен), что
выполняется условие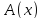 ,
содержащее
,
содержащее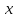 как переменную. Например, высказывание
«
как переменную. Например, высказывание
«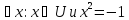 »
звучит так: найдется число
»
звучит так: найдется число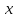 из числового множества
из числового множества ,
квадрат которого равен -1. Если подразумевать
область действительных чисел в качестве
,
квадрат которого равен -1. Если подразумевать
область действительных чисел в качестве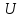 ,
то такое высказывание ложно, а для
комплексных чисел оно истинно. Итак,
знак∃заменяет
слова "существует, найдется".
,
то такое высказывание ложно, а для
комплексных чисел оно истинно. Итак,
знак∃заменяет
слова "существует, найдется".
Квантор
всеобщности ∀заменяет слова "для любого, всякий,
для каждого" и т.п. Например,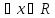 (
(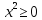 )
-- верное высказывание, а
)
-- верное высказывание, а --
ложное высказывание.
--
ложное высказывание.
Полные и противоречивые теории

Курт Фри́дрих Гёдель (нем. Kurt Friedrich Gödel; 28 апреля 1906, Брюнн, Австро-Венгрия — 14 января 1978, Принстон,Нью-Джерси) — австрийский логик, математик и философ математики, наиболее известный сформулированной и доказанной им теоремой о неполноте.
Гёдель был логиком и философом науки. Наиболее известное достижение Гёделя — это сформулированные и доказанные им теоремы о неполноте, опубликованные в 1931 году. Одна из них гласит, что любая эффективно аксиоматизируемая теория, в достаточно богатом языке, достаточном для определения натуральных чисел и операций сложения и умножения, является неполной либо противоречивой. Неполнота означает наличие высказываний, которые нельзя ни доказать, ни опровергнуть, исходя из аксиом этой теории. Противоречивость — возможность доказать любое высказывание: как истинное, так и ложное. Эффективная аксиоматизируемость понимается как возможность алгоритмически решить, является ли данное утверждение аксиомой. Доказанные Гёделем теоремы имеют широкие последствия как для математики, так и для философии (в частности, для онтологии и философии науки).
Методы доказательств.
Доказательство
«от противного»основано на том, что
для любого утверждения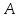 верно ровно одно из утверждений: либо
верно ровно одно из утверждений: либо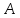 ,
либо его отрицание
,
либо его отрицание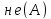 .
Это можно считать логической аксиомой.
Схема доказательства утверждения
.
Это можно считать логической аксиомой.
Схема доказательства утверждения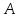 «от противного» такова: мы предполагаем,
что верно отрицание
«от противного» такова: мы предполагаем,
что верно отрицание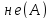 и приводим это предположение к противоречию
(типа 0=1). Тогда получается, что верно
и приводим это предположение к противоречию
(типа 0=1). Тогда получается, что верно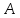 .
.
Приведем
пример: докажем, что квадрат рациональной
дроби не может быть равен 2. Предположим
противное: имеет место равенство
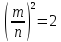 для некоторой дроби
для некоторой дроби .
Дробь
.
Дробь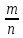 можно считать несократимой, т.е.
можно считать несократимой, т.е.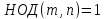 .
Но из соотношения
.
Но из соотношения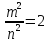 вытекает
вытекает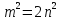 и тем самым число
и тем самым число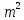 ,
а значит и число
,
а значит и число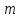 четное, т.е. делится на два:
четное, т.е. делится на два: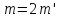 .
Действительно, если бы
.
Действительно, если бы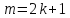 было бы нечетным, то
было бы нечетным, то было бы также нечетным, вопреки тому,
что оно четно. Подстановка
было бы также нечетным, вопреки тому,
что оно четно. Подстановка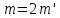 в
в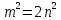 дает
дает или
или .
Аналогичные рассуждения показывают,
что число
.
Аналогичные рассуждения показывают,
что число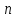 также четно, и тем самым дробь
также четно, и тем самым дробь сократима на два – противоречие с
выбором дроби. Это противоречие указывает
на ложность допущения о существовании
рационального решения уравнения
сократима на два – противоречие с
выбором дроби. Это противоречие указывает
на ложность допущения о существовании
рационального решения уравнения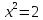 .
.
Метод
разделения случаев. Если
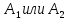 истинно, то для доказательства утверждения
истинно, то для доказательства утверждения достаточно установить справедливость
импликаций
достаточно установить справедливость
импликаций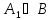 и
и .
.
Пример.
Докажем, что при любом натуральном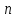 число
число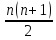 цело. Рассмотрим два исчерпывающих
случая: 1)
цело. Рассмотрим два исчерпывающих
случая: 1)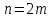 -- четно и 2)
-- четно и 2)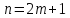 – нечетно. В первом случае
– нечетно. В первом случае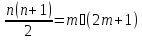 -- цело, а втором --
-- цело, а втором --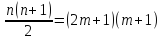 также цело.
также цело.
Метод
перехода от теоремы
 к теореме
к теореме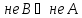 .
(см. эквивалентность (1))
.
(см. эквивалентность (1))
Пример.
Докажем, что если
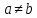 ,
то
,
то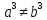 (для квадратов это не верно, почему –
см. следующий метод). Предположим
(для квадратов это не верно, почему –
см. следующий метод). Предположим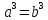 ,
тогда
,
тогда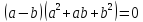 .
Произведение равно 0 если и только если
один из сомножителей равен 0. Если
.
Произведение равно 0 если и только если
один из сомножителей равен 0. Если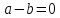 ,
то
,
то ,
что и требовалось доказать. Исследуем
случай
,
что и требовалось доказать. Исследуем
случай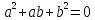 .
Так как
.
Так как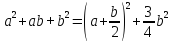 ,
то из последнего равенства вытекает,
что
,
то из последнего равенства вытекает,
что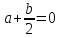 и
и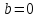 одновременно. Тогда и
одновременно. Тогда и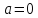 ,
т.е. опять
,
т.е. опять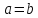 .
.
Метод
контрпримера. Для того, что бы
установить ложность утверждения достаточно указать конкретный объект
достаточно указать конкретный объект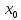 при подстановке которого утверждение
при подстановке которого утверждение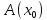 становиться ложным.
становиться ложным.
Пример.
Утверждение
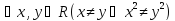 не верно как показывает контрпример:
не верно как показывает контрпример: ,
но
,
но .
.
Принцип математической индукции (ПМИ). Пусть дан ряд утверждений
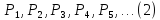
и известно, что
1)
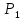 -- истинное утверждение (база индукции);
-- истинное утверждение (база индукции);
2)
если для какого-либо n утверждение
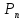 верно (индукционное предположение),
то и следующее утверждение
верно (индукционное предположение),
то и следующее утверждение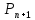 также истинно (индукционный переход)
также истинно (индукционный переход)
Тогда
ПМИ позволяет заключить, что все
утверждения
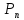 верны. Более подробно этот принцип
изложен в отдельном параграфе.
верны. Более подробно этот принцип
изложен в отдельном параграфе.
Договоримся
всюду далее знак ":=" использовать
как равенство по определению, т.е.
 означает, что
означает, что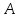 по определению равно
по определению равно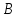 .
.
