
- •Оглавление
- •Определение определенного интеграла
- •Свойства определённого интеграла
- •Критерий интегрируемостиДарбу
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Теорема сравнения.
- •Абсолютная сходимость
- •Интегралы, зависящие от параметра
- •Гамма-функция Эйлера
- •Приближенное вычисление определённых интегралов
Гамма-функция Эйлера
Функция вида
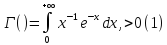
называется
гамма-функцией. Заметим прежде всего,
что интеграл (1) сходится при всех >0. Действительно, представим его в
виде суммы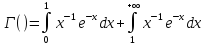 .
Первый из этих интегралов сходится так
как
.
Первый из этих интегралов сходится так
как
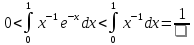
Второй
интеграл сходится, так как при x→+∞ имеет место оценка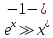 . Следовательно,
. Следовательно,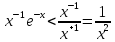 а интеграл от последней функции сходится
на +∞ .
а интеграл от последней функции сходится
на +∞ .
Свойства гамма-функции
1. Основное функциональное уравнение:
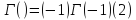
при любом >1.
2. Для любого натурального n имеет место равенство Γ (n)=(n-1)!. В частности, Γ (1)=1.
3. Гамма-функция непрерывна и имеет непрерывные производные всех порядков. Например,
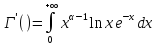
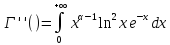
Интеграл Эйлера-Пуассона
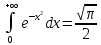
Во-первых,
этот интеграл сходится. Обозначим его
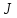 и
сделаем замену
и
сделаем замену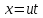 ,
где
,
где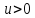 ,
а
,
а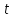 – новая переменная. Тогда
– новая переменная. Тогда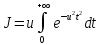 .
Умножим это равенство на
.
Умножим это равенство на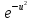 и проинтегрируем по
и проинтегрируем по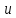 .
Получим
.
Получим
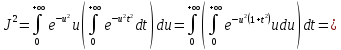
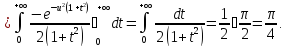
Отсюда
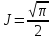 .
.
4.
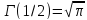 .
.
Приближенное вычисление определённых интегралов
Задана
функция
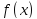 на отрезке
на отрезке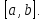 Указана точность
Указана точность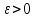 .
Требуется найти
.
Требуется найти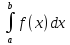 с точностью ε . Эта задача важна по тpем
пpичинам:
с точностью ε . Эта задача важна по тpем
пpичинам:
а) существуют
небеpущиеся интегpалы (напpимеp,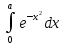 );
);
б) иногда даже "беpущийся" интегpал вычислить пpиближенно легче, чем находить пеpвообpазную и пользоваться фоpмулой Hьютона-Лейбница (напpимеp, сложная pациональная дpобь);
в) значения коэффициентов, аpгументов и pезультаты вычислений – пpиближенные, поэтому понятие "вычислить точно интегpал" - относительно.
Пусть
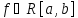 ,
,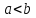 ,
,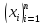 -- равномерное разбиение (узловые точки),
-- равномерное разбиение (узловые точки),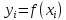 .
Тогда имеют место приближенные
.
Тогда имеют место приближенные
Формулы прямоугольников
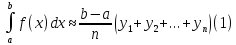
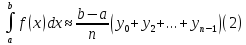
Ошибка в этих формулах равна
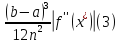
для некоторого
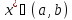 .
Отсюда вытекает оценка погрешности.
.
Отсюда вытекает оценка погрешности.
Приближая
функцию
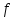 на каждом отрезке
на каждом отрезке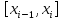 линейной функцией
линейной функцией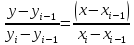 ,
получаем приближенную формулу трапеций
,
получаем приближенную формулу трапеций
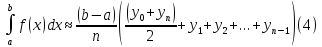
Ошибка в формуле трапеций в два раза меньше:
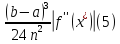
для некоторого
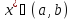 .
.
Разобьём
теперь отрезок [a,b] равномерно на четное
число подотрезков:
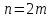 .
Тогда имеет место приближенная
.
Тогда имеет место приближенная
Формула Симпсона
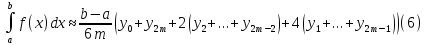
Ошибка в этой формуле равна
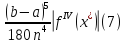
для
некоторого
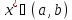 .
На практике, однако ошибку оценивают
так:
.
На практике, однако ошибку оценивают
так: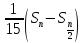 .
.
Если f -- квадратный трехчлен, то в формуле Симпсона приближённое равенство превращается в точное.
