
- •Оглавление
- •Определение определенного интеграла
- •Свойства определённого интеграла
- •Критерий интегрируемостиДарбу
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Теорема сравнения.
- •Абсолютная сходимость
- •Интегралы, зависящие от параметра
- •Гамма-функция Эйлера
- •Приближенное вычисление определённых интегралов
Критерий интегрируемостиДарбу
Предположим,
что функция
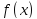 ограничена на отрезке
ограничена на отрезке (
( ).
Тогда для любого разбиения (
).
Тогда для любого разбиения ( )
этого отрезка определены числа
)
этого отрезка определены числа

Величины

называются нижней и верхней интегральной суммойсоответственно. Имеет место неравенство

для любой
системы отмеченных точек
 .
Так как точная нижняя грань на подотрезке
больше или равна точной нижней грани
на отрезке, а точная верхняя грань на
подотрезке меньше или равна точной
верхней грани на отрезке, то при
измельчении разбиения нижняя интегральная
сумма увеличивается, а верхняя уменьшается
.
Так как точная нижняя грань на подотрезке
больше или равна точной нижней грани
на отрезке, а точная верхняя грань на
подотрезке меньше или равна точной
верхней грани на отрезке, то при
измельчении разбиения нижняя интегральная
сумма увеличивается, а верхняя уменьшается
Следствие.Существуют пределы
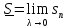 ;
;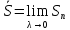 ;
;
которые называются нижним и верхним интегралом.
Теорема
1.Интеграл
 существует тогда и только тогда, когда
нижний интеграл совпадает с верхним
интегралом (
существует тогда и только тогда, когда
нижний интеграл совпадает с верхним
интегралом ( ).
В этом случае все три интеграла совпадают.
).
В этом случае все три интеграла совпадают.
Доказательство. Импликация "тогда" следует из теоремы о пределе промежуточной последовательности и неравенств (2).
Докажем
обратную импликацию. Пусть интеграл
равен
 .
Предположим, чтоS≠
.
Предположим, чтоS≠ .
Тогда
.
Тогда ,
и, кроме того,
,
и, кроме того,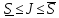 .
Выберем разбиение отрезка [a,b] с таким
малым значением параметра,
что
.
Выберем разбиение отрезка [a,b] с таким
малым значением параметра,
что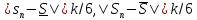 и
и

для любой
системы отмеченных точек
 .
Можно выбрать системы (ξi) и (νi)
отмеченных точек так, что
.
Можно выбрать системы (ξi) и (νi)
отмеченных точек так, что
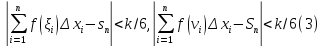
Применяя
неравенство треугольника, из соотношений
(3) получаем
 .
.
Тогда

следовательно,
 .
Это противоречие показывает, что на
самом деле нижний интеграл равен верхнему
интегралу.□
.
Это противоречие показывает, что на
самом деле нижний интеграл равен верхнему
интегралу.□
Пример.Пусть

(функция
Дирихле). Эта функция не интегрируема
ни на каком отрезке, так как S=0,
но .
.
Функция
называется кусочно-непрерывной на
отрезке
 ,
если этот отрезок можно разбить на
конечное число подотрезков точками
,
если этот отрезок можно разбить на
конечное число подотрезков точками так, что в каждой из точек
так, что в каждой из точек функция имеет односторонние пределы,
а в остальных точках отрезка
функция имеет односторонние пределы,
а в остальных точках отрезка функция непрерывна.
функция непрерывна.
Теорема 2. Кусочно-непрерывная функция интегрируема на любом отрезке.
Доказательство.
Аддитивность интеграла и его
нечувствительность к изменению функции
в конечном числе точек (см. предыдущий
параграф) позволяют свести доказательство
теоремы к случаю, когда
 -- непрерывная функция. Непрерывная
функция на отрезке равномерно непрерывна
(«Введение в анализ»). Это значит, что
для любого
-- непрерывная функция. Непрерывная
функция на отрезке равномерно непрерывна
(«Введение в анализ»). Это значит, что
для любого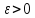 найдется
найдется такое, что
такое, что как только
как только и
и Пусть
Пусть -- разбиение отрезка
-- разбиение отрезка с параметром меньшим чем
с параметром меньшим чем ,
а
,
а -- две системы отмеченных точек. Тогда
-- две системы отмеченных точек. Тогда

Отсюда
следует, что верхняя интегральная сумма
 отличается от нижней
отличается от нижней не более чем на
не более чем на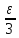 .
Можно считать, что
.
Можно считать, что настолько мало, что
настолько мало, что и
и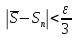 как только параметр разбиения меньше
чем
как только параметр разбиения меньше
чем .
Тогда
.
Тогда

Итак,
 каково бы мало ни была положительная
величина
каково бы мало ни была положительная
величина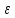 .
Это может быть лишь в случае
.
Это может быть лишь в случае . Остаётся применить теорему 1 .□
. Остаётся применить теорему 1 .□
Формула Ньютона-Лейбница
Интеграл
вида
 называют интегралом с переменным
верхним пределом.
называют интегралом с переменным
верхним пределом.
Теорема.
Пусть функция
 непрерывна на отрезке
непрерывна на отрезке .
Тогда
.
Тогда есть первообразная функции
есть первообразная функции
 :
:

для любого
 .
.
Доказательство.
Пусть
 .
Тогда по теореме о среднем
.
Тогда по теореме о среднем

для некоторой
точки Следовательно,
Следовательно,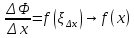 при
при ,
ибо в этом случае
,
ибо в этом случае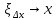 ,
а функция
,
а функция непрерывна.□
непрерывна.□
Формула
Ньютона-Лейбница. Пусть
 -- первообразная функции
-- первообразная функции .
Тогда
.
Тогда
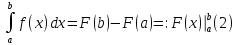
Доказательство.
Для функции
 имеем в распоряжении две первообразных
имеем в распоряжении две первообразных и
и . По теореме о первообразных (см.§
Error: Reference source not found )найдется константа
. По теореме о первообразных (см.§
Error: Reference source not found )найдется константа такая, что
такая, что

Подставим
в соотношение (3) вместо
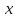 сначала
сначала и получим
и получим ,
а затем подставим
,
а затем подставим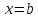 в (3) – получим
в (3) – получим

что и требовалось доказать.
Пример.
 (см. пример вычисления площади в начале§1).
(см. пример вычисления площади в начале§1).
Замечание. Можно было бы определить логарифм так:

т.е. фактически
как первообразную функции
 ,
примимающую в точке 1 значение 0. Нетрудно
доказать основное правило обращения с
логарифмами:
,
примимающую в точке 1 значение 0. Нетрудно
доказать основное правило обращения с
логарифмами:

Действительно,

Тогда
 – это такое число
– это такое число ,
что
,
что (т.е. площадь под гиперболой равна 1), а
(т.е. площадь под гиперболой равна 1), а --
функция обратная к
--
функция обратная к .
.
