
- •Оглавление
- •Определение определенного интеграла
- •Свойства определённого интеграла
- •Критерий интегрируемостиДарбу
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Теорема сравнения.
- •Абсолютная сходимость
- •Интегралы, зависящие от параметра
- •Гамма-функция Эйлера
- •Приближенное вычисление определённых интегралов
Свойства определённого интеграла
Перейдем к изучению простейших свойств определенного интеграла.
Свойство
линейности.Сумма интегрируемых
функций есть интегрируемая функция и
произведение интегрируемой функции на
число есть также интегрируемая функция.
Более того, если интегрируемы, то для любых чисел
интегрируемы, то для любых чисел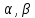 линейная комбинация
линейная комбинация также интегрируема на отрезке
также интегрируема на отрезке и
и

Равенство (4) эквивалентно двум правилам: 1) интеграл от суммы функций равен сумме интегралов и 2) постоянный множитель можно выносить за знак интеграла.
Это свойство следует из соответствующих свойств предела – предел суммы равен сумме пределов и постоянный множитель можно вносить за знак предела.
Изменение
ориентации.Равенство справедливо вне зависимости от
расположения точек
справедливо вне зависимости от
расположения точек и
и на числовой прямой.
на числовой прямой.
Не
чувствительность интеграла к изменению
значений подинтегральной функции в
конечном числе точек: на существование
и на значение определенного интеграла
не влияет изменение значения функции в конечном числе точек.
в конечном числе точек.
Действительно,
рассмотрим функцию
 равную нулю всюду за исключением точки
равную нулю всюду за исключением точки ,
в которой эта функция равна единице.
Пусть
,
в которой эта функция равна единице.
Пусть .
Интегральная сумма этой функции равна
либо 0, либо
.
Интегральная сумма этой функции равна
либо 0, либо (если
(если совпадает с одной из отмеченных точек).
Следовательно, эта интегральная сумма
стремиться к нулю при
совпадает с одной из отмеченных точек).
Следовательно, эта интегральная сумма
стремиться к нулю при Иными словами,
Иными словами, .
Теперь заметим, что для замены значения
функции
.
Теперь заметим, что для замены значения
функции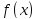 в точке
в точке с
с на
на нужно образовать линейную комбинацию
нужно образовать линейную комбинацию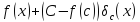 .
Если
.
Если интегрируема
на отрезке
интегрируема
на отрезке ,
то и эта линейная комбинация интегрируема,
и значение интеграла не меняется в силу
(4).
,
то и эта линейная комбинация интегрируема,
и значение интеграла не меняется в силу
(4).
Из возможности изменения значения функции в одной точки следует возможность изменения значений функции в конечном числе точек.
Аддитивность
интеграла. Пусть
 .
Тогда функция
.
Тогда функция интегрируема на отрезке
интегрируема на отрезке в том и только том случае, когда она
интегрируема на
в том и только том случае, когда она
интегрируема на и на
и на .
В этом случае
.
В этом случае

Если точки
 расположены произвольно на числовой
прямой и каждый из интегралов в (5)
существует, то равенство (5) имеет место.
расположены произвольно на числовой
прямой и каждый из интегралов в (5)
существует, то равенство (5) имеет место.
Доказательство.
Обозначим
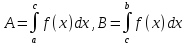 ,
предполагая, что эти интегралы существуют.
По доказанному выше функция
,
предполагая, что эти интегралы существуют.
По доказанному выше функция ограничена на отрезках
ограничена на отрезках и
и ,
а, значит, ограничена и на отрезке
,
а, значит, ограничена и на отрезке Пусть
Пусть для любого
для любого Выберем
Выберем .
Интегральные суммы функции
.
Интегральные суммы функции на отрезках
на отрезках и
и обозначим
обозначим и
и соответственно. Найдем
соответственно. Найдем такое, что
такое, что

если
параметры соответствующих разбиений
меньше
 .
Если надо, уменьшим
.
Если надо, уменьшим так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство Рассмотрим теперь произвольное разбиение
(1) отрезка
Рассмотрим теперь произвольное разбиение
(1) отрезка с параметром меньшим чем
с параметром меньшим чем ,
и обозначим интегральную сумму для
этого разбиения с произвольно взятыми
отмеченными точками как
,
и обозначим интегральную сумму для
этого разбиения с произвольно взятыми
отмеченными точками как .
Добавим к разбиению (1) точку
.
Добавим к разбиению (1) точку ,
если
,
если ни для какого
ни для какого .
От этого параметр разбиения не увеличится.
Добавим также еще одну отмеченную точку.
Тогда интегральная сумма
.
От этого параметр разбиения не увеличится.
Добавим также еще одну отмеченную точку.
Тогда интегральная сумма изменится самое большее на величину
изменится самое большее на величину ,
но эту новую интегральную сумму можно
будет разбить на две интегральные суммы
,
но эту новую интегральную сумму можно
будет разбить на две интегральные суммы и
и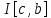 на отрезках
на отрезках и
и ,
которые удовлетворяют неравенствам
(6). Тогда
,
которые удовлетворяют неравенствам
(6). Тогда

По определению
предела получаем, что
 Тем самым
Тем самым .
.
Наоборот,
пусть
 и
и .
Докажем, что функция
.
Докажем, что функция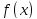 интегрируема на подотрезке
интегрируема на подотрезке .
Понадобиться критерий Коши. Обозначим
.
Понадобиться критерий Коши. Обозначим Для заданного
Для заданного найдем
найдем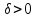 такой, что
такой, что ,
как только параметр разбиения меньше
чем
,
как только параметр разбиения меньше
чем Рассмотрим два разбиения отрезка
Рассмотрим два разбиения отрезка с параметрами меньшими
с параметрами меньшими и пусть
и пусть и
и – соответствующие им две интегральные
суммы. Продолжим рассматриваемые
разбиения и интегральные суммы на весь
отрезок
– соответствующие им две интегральные
суммы. Продолжим рассматриваемые
разбиения и интегральные суммы на весь
отрезок с условием совпадения их и отмеченных
точек на отрезке
с условием совпадения их и отмеченных
точек на отрезке ,
а также сохранением неравенства
,
а также сохранением неравенства Продолжения обозначим
Продолжения обозначим и
и .
Тогда
.
Тогда

Мы проверили
условия критерия Коши. Согласно этому
критерию получаем, что существует предел
интегральных сумм
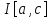 при
при .
Аналогично,
.
Аналогично, .
По доказанному выше, получаем равенство
(5).
.
По доказанному выше, получаем равенство
(5).
Рассмотрим
случай
 расположения точек
расположения точек .
Тогда по условию и доказанному выше
имеет место равенство
.
Тогда по условию и доказанному выше
имеет место равенство . Перенося
. Перенося в левую часть и заменяя
в левую часть и заменяя на
на получаем
получаем ,
что совпадает с (5). Аналогично разбираются
другие случаи расположения точек
,
что совпадает с (5). Аналогично разбираются
другие случаи расположения точек .
.
Аддитивность интеграла полностью доказана. □
Монотонность
интеграла.Если для всех
для всех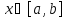 и
и ,
то
,
то .
.
Действительно,
в этом случае
 и переходя к пределу
и переходя к пределу в этом неравенстве (см. раздел «Предел
и непрерывность»), получаем искомое
соотношение между интегралами.
в этом неравенстве (см. раздел «Предел
и непрерывность»), получаем искомое
соотношение между интегралами.
Интеграл от единицы. Как следующее свойство отметим одно простое равенство, вытекающее из определения определенного интеграла:
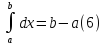
Оценка
интеграла.Если на отрезке
на отрезке и
и ,
то
,
то

Действительно,
 Здесь мы последовательно применили
монотонность интеграла, его линейность
и равенство (6). Аналогично доказывается
первое из неравенств в (7).
Здесь мы последовательно применили
монотонность интеграла, его линейность
и равенство (6). Аналогично доказывается
первое из неравенств в (7).
Например,
 на отрезке
на отрезке ,
что следует из монотонности функции
,
что следует из монотонности функции а значит и функции
а значит и функции . Отсюда,
. Отсюда,

Теорема о среднем. Если функция непрерывна на отрезке
непрерывна на отрезке ,
то найдётся точка
,
то найдётся точка такая,
что
такая,
что

Величина
 называетсяинтегральным средним
функции
называетсяинтегральным средним
функции
 на отрезке
на отрезке .
.
Доказательство.
По теореме Вейерштрасса, функция
 на отрезке
на отрезке достигает своего наибольшего значения
достигает своего наибольшего значения )
и наименьшего значения
)
и наименьшего значения .
Здесь
.
Здесь -- некоторые точки отрезка
-- некоторые точки отрезка .
Применяя оценку интеграла (7), выводим
.
Применяя оценку интеграла (7), выводим

Интегральное
среднее оказывается промежуточным
значением между наименьшим и наибольшим
значениями. Применим теорему Больцано-Коши
о промежуточном значении к непрерывной
функции
 и найдем точку
и найдем точку между
между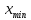 и
и (значит
(значит )
такую, что
)
такую, что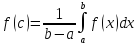 .□
.□
Пример. Пусть

Тогда
интегральное среднее функции (9) на
отрезке
 равно
равно

Однако
точки
 такой, что
такой, что нет. Причина этого – разрыв функции
нет. Причина этого – разрыв функции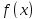 в точке 1.
в точке 1.
