Matematicheskaya_logika

3. Полные системы связок. Нормальные формы.

Не только всякая пропозициональная форма определяет истинностную функцию, но верно и обратное утверждение.

Предложение 5. Всякая истинностная функция определяется пропозициональной формой, содержащей только связки ,&, .

Доказательство. Пусть задана истинностная функция f(x1,...,xn) при помощи

таблицы истинности, имеющей 2n строк, которые занумеруем посредством 1,2,

..., 2n.

Для каждой i - ой строчки рассмотрим конъюнкции Сi: U1i&U2i&...&Uni,(i =1,2,…,2n),

где

Тогда пропозициональная форма D, представляющая дизъюнкцию всех Ci,, построенных для тех строк, где функция f принимает значение истина,, определяет функцию f. То есть, D и f принимают одинаковые истинностные значения в соответствующих строчках

Действительно. Если в некотором k-том распределении f принимает значение И, то Ck, которое при этом распределения в силу определения тоже истинно, является дизъюнктивным членом D. Поэтому D тоже истинна.

Заметим, что при k-ом распределении все другие конъюнкции кроме Сk принимают значение ложь.

Поэтому, если в k - ой строке f принимает значение ложь, то Сk в D не входит, а входят другие конъюнкции, принимающие при этом распределении ложные значения, тогда и дизъюнкция D принимает значение ложь.

Таким образом, D определяет функцию f.

Определение. Пропозициональная форма называется дизъюнктивной нормальной формой (ДНФ), если является дизъюнкцией конъюнкций.

Если при этом в каждом дизъюнктивном члене содержится любая буква или её отрицание, то пропозициональная форма называется совершенной дизъюнктивной нормальной формой (СДНФ).

Так как функция принимает значение И в 1, 4, 6 и 7 строчках, то D имеет вид C1 C4 C6 C7 ,

то есть А1&А2&А3 ¬А1& ¬А2&А3 А1&А2& А3 А1& ¬А2& ¬ А3, которая является совершенной дизъюнктивной нормальной формой.

Замечание. Аналогично при помощи строчек, в которых функция принимает значение Л можно построить совершенную конъюктивную нормальную форму.

Заметим, что последовательное соединение ----------/А------/В---------двух контактов А и В можно выразить ( реализовать ) при помощи конъюнкции А&В, а

параллельное соединение

А

B

реализуется при помощи дизъюнкции А В.

Таким образом, в силу предложения 5, при помощи электрической цепи, называемой релейно-контактной схемой ( РКС ). можно реализовать любую истинностную функцию.

Например, Если предварительно упростить пропозициональную форму из

Следствие 1. Любую истинную функцию можно определить при помощи пропозициональной формы, содержащей только одну из следующих трех пар связок: ¬, &; ¬, ; ¬, →.

Доказательство. Учитывая предложение 5, в силу предложения 4, при помощи равносильности А В ¬( ¬А& ¬В) получаем достаточность первой пары связок: ¬, &.для построения всех истинностных функций .

При помощи равносильности А& В ¬( ¬А ¬В) получаем достаточность второй пары связок: ¬, .

При помощи равносильностей А&В ¬(А→ ¬В) и А В ¬А→В получаем достаточность третьей пары связок: ¬, →.

Чтобы ответить на вопрос о возможности порождения всех истинностных функций при помощи одной связки рассмотрим связку ↓( стрелка Пирса ) и связку | ( штрих Шеффера ), которые определяются при помощи следующей

Следствие 2. Единственными бинарными связками, каждой из которых достаточно для выражения всех истинностных функций, являются ↓ и | .

h(A,B), которая является достаточной для выражения всех истинностных функций. h(И,И) должно быть Л, так как в противном случае не возможно выразить

функцию отрицания. Аналогично , h(Л,Л) должно быть И.

Так как при помощи ¬ можно выразить только переменную или ее отрицание, но нельзя выразить функцию, принимающую только истинные значения, то стрелка Пирса и штрих Шеффера являются единственными связками в указанном смысле.

Нормальные формы.

1. Постройте совершенную дизъюнктивную нормальную форму логически эквивалентную пропозициональной форме:

a)¬А& B →C ¬B ↔(A→B)

D- совершенная дизъюнктивная нормальная форма, если в каждый ее дизъюнктивный член входит каждая из возможных букв или ее отрицание.

если ее не было, то поставить перед каждой буквой. 4. Для формы F постройте КНФ.

F¬A& B & ¬C A& B &C A& ¬B & ¬C A& ¬B & ¬C

A& B &¬¬C;

Постройте СДНФ для:

F (A B ¬C) & (¬A ¬B ¬C) & (A ¬B C) & (¬A ¬B C).

Упрощение систем высказываний.

13. Упростите директивы, если по крайней мере одна из них должна быть выполнена:

1)Инспектору не разрешается курить на заводе.

2)Если инспектору разрешить курить на заводе, то рабочие должны быть предупреждены и бригадир должен принять меры.

3)Рабочие должны быть предупреждены или бригадир должен принять еры.

4)Или рабочие должны быть предупреждены и бригадир должен принять меры или инспектору не разрешается курить на заводе.

14.1) Будут приобретены палатки, рюкзаки и мы пойдем в поход.

2)Палатки и рюкзаки приобретены не будут, и мы не пойдем в поход.

3)Будут приобретены палатки, рюкзаки не будут, мы пойдем в поход.

4)Не верно, что, либо будут приобретены палатки, либо не будут приобретены рюкзаки, либо мы в поход не пойдем.

Логические задачи.

15. Или Витя, или Коля, или Толя разбил окно.

1)«Это мог сделать только один Витя, или Толя»,- сказал Андрей.

2)«Я окно не разбивал»,- возразил Витя и Коля тоже.

3)«Вы оба говорите неправду»,- заявил Толя.

4)«Нет, Толя, один из них сказал правду, а другой сказал неправду»,- возразил Дима.

5)«Ты Дима, не прав», - сказал Коля.

Трое сказали правду. Кто разбил окно?

16. Четыре друга, Антон, Влад, Семен и Дима, решили провести отпуск в Москве, Лондоне, Киеве и в Ташкенте. В какой город поедут каждый из них, если известны следующие ограничения:

Р Если Антон не едет в Москву, то Семен не едет в Лондон.

QЕсли Влад не едет ни в Москву, ни в Ташкент, то Антон. едет в Москву.

RЕсли Семен не едет в Ташкент, то Влад едет в Киев.

SЕсли Дима не едет в Москву, то Влад едет в Москву.

Т Если Дима не едет в Лондон, то Влад не едет в Москву.

4. Формальные теории.

Теория Р считается формально определенной , если: 1. Выделено счетное множество символов.

Причём, конечная последовательность символов называется выражением.

2.Среди множества выражений выделено множество формул. Обычно существует алгоритм, распознающий выражения на формулу.

3.Среди множества формул выделено множество аксиом.

Если существует алгоритм распознания формулы на аксиому, то теория называется аксиоматической (или эффективно аксиоматизированной).

4. Выделено множество отношений R1, R2, ..., Rn, называемых правилами вывода. Причём для каждого Ri существует j такое, что для некоторой формулы A и произвольных j формул можно определять находится ли она в отношении Ri с этими j формулами или нет. Если находится, то формула A называется

непосредственным следствием этих j формул по правилу вывода Ri.

Выводом формулы А в теории Р называется конечная последовательность формул А1, ..., An, которая заканчивается на A и в которой для любого i ( i=1,…,n) Ai либо

1)аксиома, либо

2)непосредственное следствие предыдущих формул по некоторому правилу вывода.

Если существует эффективная процедура распознания формул на теорему, то теория называется разрешимой.

Выводом формулы А из множества формул Г (Г РА) называется конечная последовательность А1, А2, ..., Аn, которая заканчивается на A и такая, что для любого i= 1,2,…,n Ai либо

1)аксиома, либо

2)гипотеза (Ai принадлежит множеству формул Г), либо

3)непосредственное следствие предыдущих формул по некоторому правилу вывода.

Свойства.

1.Если из множества формул Г выводима в теории Р формула A и Г является подмножеством множества формул ∆ , то из множества формул ∆ выводима формула A.

2.Из множества формул ∆ выводима формула A тогда и только когда, когда существует конечное подмножество Г множества ∆ , из которого выводима формула A.

3.Если из множества формул Г выводима в теории Р формула A и из множества

формул ∆ выводима любая формула из Г, то из множества формул ∆ выводима формула A.

Доказательство. 1 свойство выполняется так как всякая гипотеза по причине принадлежности множеству Г в выводе формулы A из Г по условию является формулой множества ∆ .

Достаточное условие 2 свойства следует из 1 свойства. А необходимое из того, что вывод, являясь конечной последовательностью формул, содержит конечное множество гипотез, из которых образуется множество ∆ .

Для доказательства 3 свойства достаточно в выводе формулы A из множества Г заменить все гипотезы на их выводы из множества ∆ , что возможно в силу условия.

5 Исчисление высказываний.

Исчисление высказываний (теорию L) определим так: 1.Символами теории L являются , →, ( , ), А, В, С, .…

2.Формулами теории L являются пропозициональные формы, содержащие только

¬и →.

3.Три схемы аксиом: (А1) А→(В→А)

(А2) (А→(В→С)) →((А→В) →(А→С)) (А3) ( ¬В→ А) →(( В→А) →В)

порождают бесконечное множество аксиом теории L при произвольных формулах А, В и С.

4. Единственным правилом вывода является Modus ponens (MP): В является непосредственным следствием формул А и А→В, то есть А, А→В В.

Доказательство:

1)(А→((А→А) →А)) →((А→(А→А)) (А2)

2)(А→((А→А) →А) (А1)

3)(А→(А→А)) →(А→А) (2,1,МР)

4)А→(А→А) (А1)

5)А→А (3,4,МР)

По выводу 1) - 5) имеем L А→А.

Теорема дедукции. Если из множество формул Г и формулы А выводима формула

В ( Г, А L В ) , то Г L А→В. ( В частности , если А LВ, то L А → В).

Доказательство: Пусть В1,В2, ..., Вn - В является выводом формулы В из множества формул Г и формулы А. Тогда для любого i =1,2,…, n имеем

1) Bi – аксиома, либо

2) Bi – гипотеза, то есть

3)Bi - непосредственное следствие предыдущих формул Вj и Вk по правилу МР, причем Вk - Вj →Вi .

Докажем утверждение теоремы индукцией по длине вывода i, то есть докажем,

что Г А→Вi . Тогда при I=n утверждение будет справедливо для формулы B. I. При i =1 докажем, что Г А→В1 .

2.2.В1 - А, тогда , учитывая лемму и 1 свойство выводимости , имеем

Г А→В1.

Всилу невозможности случая 3) базис рассмотрен.

II. Предполагаем, что утверждение справедливо для формул Вl с номерами l меньшими i и докажем для Вi.

Если 1) Вi аксиома или

2)гипотеза, то доказательство совпадает с базисным с заменой В1 на Вi

3)Вi непосредственное следствие предыдущих формул Вj и Вk - Вj →Вi, то из того, что j<i, k<i по индуктивному предположению имеем, что

Г А→ (Вj →Вi) и Г А→ Вj.

По аксиоме (А2) имеем, что из Г (А→ (Вj →Вi)) → ((А→ Вj) → (А→Вi)).

Применим МР дважды. Тогда получим, что Г А→Вi.

Таким образом, по аксиоме индукции утверждение теоремы справедливо для любого i, а поэтому и для формулы B.

Следствие 1. А→В, В→С А →С.

Доказательство: 1) А→В (гип.)

По 1) – 5) имеем А→В, В→С, А С.

Поэтому по теореме дедукции А→В, В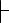→С А →С.

Следствие 2. А→(В→С), В 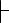А →С.

Доказательство: 1) А→(В→С) (гип.)

2)В (гип.)

3)А (гип.)

4)В→С (1, 3, МР)

5)С (2, 4, МР)

По 1) – 5) имеем А→(В→С), В, А 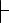С . Поэтому по теореме дедукции А→В, В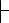→С А →С.

6. Теоремы теории L

Лемма Для любых формул А и В следующие формулы являются теоремами теории L:

a)¬ ¬ B →B

b)B → ¬ ¬ B

c)¬ A →(A →B)

d)( ¬ B → ¬ A) →(A →B)

e)(A →B) →( ¬ B → ¬ A)

f)A →( ¬ B → ¬(A →B))

g)(A →B) →(( ¬ A →B) →B)

Доказательство:

а) 1) ( ¬В→ ¬ ¬В) →( В→ ¬В) →В) (А3)

2)¬В→ ¬В (лемма)

3)( ¬В→ ¬ ¬В) →В (1, 2, следствие 2)

4)¬ ¬В→( ¬В→ ¬ ¬В) (А1)

5)¬ ¬В→В (4, 3, следствие 1)

По 1) - 5) имеем ¬ ¬В→В

b) 1) ( ¬ ¬ ¬В→ ¬В) →(( ¬ ¬ ¬В→В) → В) (А3)

2)¬ ¬ ¬В→ ¬В (лемма а)

3)( ¬ ¬ ¬В→В) → ¬ ¬В (1, 2, МР)

4)В→( ¬ ¬ ¬В→В) (А1)

5)В→ ¬ ¬В (4, 3, следствие 1)

По 1) - 5) имеем В→ ¬ ¬В

c)1) ¬А (гипотеза)

2)А (гипотеза)

3)( ¬В→ ¬А) →(( В→А) →В) (А3)

4)¬А→( ¬В→ ¬А) (А1)

5)¬В→ ¬А (1, 4, МР)

6)( ¬В→А) →В (3, 5, МР)

7)А→( ¬В→А) (А1)

8)¬В→А (2, 7, МР)

9)В (6, 8, МР)

дважды получаем утверждение леммы c).

d)1) ¬В→ ¬А (гипотеза)

2)( ¬В→ ¬А) →(( В→А) →В) (А3)

3)( ¬В→А) →В (1, 2, МР)

4)А→( ¬В→А) (А1)

5)А→В (4, 3, следствие 1)

По 1) – 5) имеем ¬В→ ¬А А→В. Поэтому по теореме дедукции получаем

( ¬В→ ¬А) →(А→В)

e)1) А→В (гипотеза.)

2)( ¬ ¬А→ ¬ ¬В) →( ¬В→ ¬А) ( лемма d )

3)¬ ¬А→A ( лемма а )

4)¬ ¬А→B ( 3, 1, следствие 1 )